Интегрирующее звено
Интегрирующим звеном называется типовое звено, которое описывается уравнением
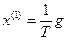 (5.27)
(5.27)
или x(1) = kg , (5.28)
где 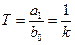 - «постоянная времени» звена, имеющая размерность времени лишь при одинаковых размерностях величин x и g ;
- «постоянная времени» звена, имеющая размерность времени лишь при одинаковых размерностях величин x и g ;
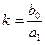 - передаточный коэффициент звена, характеризующий отношение скорости изменения выходной величины x(1) к входной величине g .
- передаточный коэффициент звена, характеризующий отношение скорости изменения выходной величины x(1) к входной величине g .
Иногда уравнение интегрирующего звена записывают в виде
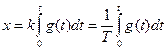 , (5.29)
, (5.29)
т.е. выходная величина является интегралом от входной величины.
Передаточная функция интегрирующего звена имеет вид
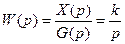 (5.30)
(5.30)
или
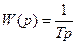 . (5.31)
. (5.31)
Полагая в выражениях (5.30) и (5.31) p=jw, получим выражение для частотной передаточной функции звена
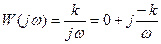 . (5.32)
. (5.32)
Совершенно очевидно, что вещественная частотная характеристика U(w)=0, а мнимая частотная характеристика 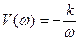 .
.
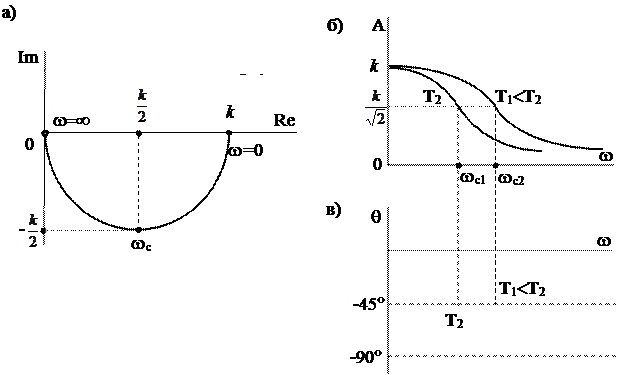
Пользуясь выражением (5.32) и изменяя частоту w от 0 до ¥, построим амплитудно-фазовую характеристику (АФХ). Очевидно, конец вектора W(jw) движется по отрицательной части мнимой оси от -¥ до 0 (рис.5.10,а).
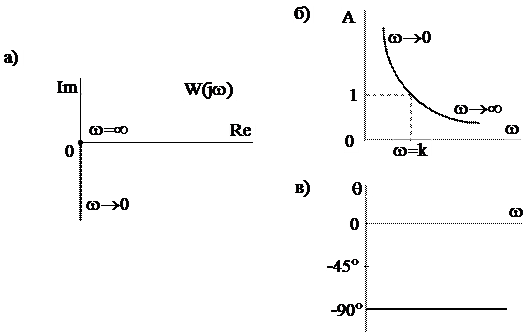 |
Рис.5.10. Частотные характеристики интегрирующего звена:
а - амплитудно-фазовая; б - амплитудная, в - фазовая
Амплитудная и фазовая частотные характеристики определяются соответственно выражениями:
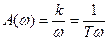 (5.33)
(5.33)
и
q(w) = arctg (-¥) = -90° . (5.34)
Из выражения (5.33) следует, что при w®0 A(w)®¥, при 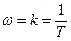 A(w)=1, а при w®¥ A(w)®0, т.е. амплитуда выходного сигнала x(t) интегрирующего звена при неизменной по величине амплитуде входного сигнала g(t) будет тем меньше, чем больше частота входного сигнала. Из выражения (5.34) следует, что фаза выходного сигнала звена на всех частотах отстает на 90° от фазы входного сигнала. Интегрирующее звено, таким образом, создает отставание (запаздывание) по фазе выходного сигнала относительно входного сигнала независимо от частоты. Графики амплитудной и фазовой частотных характеристик приведены на рис.5.10,б,в.
A(w)=1, а при w®¥ A(w)®0, т.е. амплитуда выходного сигнала x(t) интегрирующего звена при неизменной по величине амплитуде входного сигнала g(t) будет тем меньше, чем больше частота входного сигнала. Из выражения (5.34) следует, что фаза выходного сигнала звена на всех частотах отстает на 90° от фазы входного сигнала. Интегрирующее звено, таким образом, создает отставание (запаздывание) по фазе выходного сигнала относительно входного сигнала независимо от частоты. Графики амплитудной и фазовой частотных характеристик приведены на рис.5.10,б,в.
Как следует из рис.5.10,б и выражения (5.33), характеристика A(w) является разносторонней гиперболой, асимптотами которой служат оси координат.
Логарифмические частотные характеристики интегрирующего звена определяются выражениями:
L(w) = 20 lg A(w) = 20 lg k – 20 lg w (5.35)
и
j(w) = arctg (-¥) = -90° . (5.36)
Нетрудно показать, что ЛАЧХ звена является прямой с наклоном –20 дБ\дек, которая при k=1 пересекает ось частот в точке w=1. Действительно, полагая k=1, получим уравнение прямой L(w) = –20lgw, где w - переменная величина.
Изменим частоту wi в 10 раз и найдем значение ЛАЧХ, соответствующее частоте 10wi , т.е. L(10wi). Определяя разность значений ЛАЧХ в точках w=wi и w=10wi , получим
L(10wi) – L(wi) = -20 lg 10wi + 20 lg wi = -20 дБ.
Следовательно, наклон L(w) интегрирующего звена равен –20дБ\дек. Если k¹1, то характеристика смещается параллельно самой себе на 20lgk вверх при k>1 или вниз при k<1 (рис.5.11, а).
Логарифмическая фазовая частотная характеристика (ЛФЧХ) j(w) представляет собой прямую, параллельную оси частот и удаленную от нее в выбранном масштабе по оси ординат на величину -90° (рис.5.11, б).
Приведем примеры элементов САУ, которые по своим динамическим свойствам могут рассматриваться как интегрирующие звенья.
 1. Малоинерционный двигатель постоянного тока с независимым возбуждением (рис.5.12, а).
1. Малоинерционный двигатель постоянного тока с независимым возбуждением (рис.5.12, а).
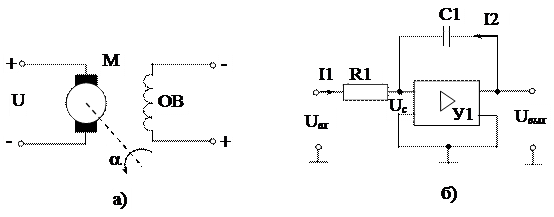 Рис.5.11. Логарифмические частотные характеристики интегрирующего звена
Рис.5.11. Логарифмические частотные характеристики интегрирующего звена
Рис.5.12. Примеры интегрирующих звеньев
Если можно пренебречь влиянием на переходный процесс двигателя момента инерции J подвижных частей в силу его малости, т.е. пренебречь величиной электромеханической постоянной времени двигателя Тэм , то
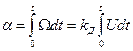 .
.
Это уравнение является уравнением интегрирующего звена, входной величиной которого является напряжение U , выходной - a (угол поворота вала двигателя).
2. Электронный усилитель постоянного тока (УПТ) с большим коэффициентом усиления по напряжению и с конденсатором в цепи отрицательной обратной связи (рис.5.12,б).
Учитывая, что Uвых(p)=-kуUс(p) , где знак «минус» означает, что полярность выходного напряжения изменяется на противоположную по сравнению с полярностью напряжения Uс за счет нечетного числа каскадов УПТ, и подставляя L1(p) и L2(p) в первое уравнение, получим
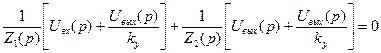 .
.
Так как коэффициент усиления kу>>1 (например, у выпускаемых отечественной промышленностью УПТ kу=1×108¸1016 , то можно записать:
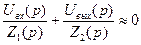
или
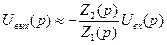 ,
,
где Z1(p) и Z2(p) – символические (операторные) сопротивления входного сопротивления усилителя и конденсатора в цепи обратной связи усилителя: Z1(p)=R1 ; Z2(p)=1/pC1 .
Теперь найдем передаточную функцию усилителя
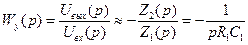 .
.
Видим, что это – передаточная функция интегрирующего звена с постоянной времени Т= R1 C1.
 |
Дата добавления: 2015-12-11; просмотров: 2913;
