Так, если САУ описывается дифференциальным уравнением. Передаточные функции САУ

Передаточные функции САУ

Для исследования и описания свойств САУ широко используются дифференциальные уравнения и их решения. Однако иногда более удобным оказывается описание динамических свойств САУ с помощью передаточных функций, которые являются результатом преобразования Лапласа линейных дифференциальных уравнений САУ.

Передаточной функцией САУ 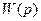называется отношение изображения по Лапласу выходной величины к изображению по Лапласу входной при нулевых начальных условиях.

Так, если САУ описывается дифференциальным уравнением

,

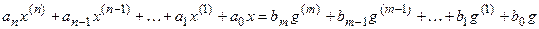то при начальных условиях

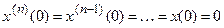
операторная форма его записи имеет следующий вид:

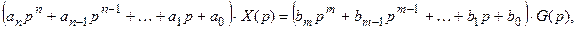
а передаточная функция определяется как

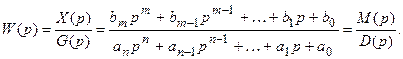
(4.1)

Здесь 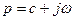– аргумент преобразования Лапласа;

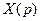и 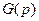– изображения функци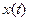й и 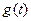по Лапласу.

Передаточная функция является своеобразной формой записи дифференциального уравнения устройства и полностью отражает его динамические свойства. Поэтому передаточная функция САУ зависит не от вида воздействия, а от параметров функциональных элементов, составляющих САУ.

Многочлен 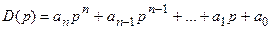называется характеристическим, и уравнение 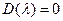называется характеристическим уравнением.

Многочлены 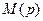и 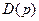могут быть представлены следующим образом:

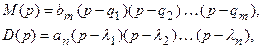
где 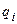– корни уравнения 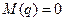– нули передаточной функции;

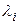– корни уравнения 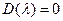– полюсы передаточной функции.

Передаточные функции сложных систем легко могут быть определены через передаточные функции составляющих их элементов (будет показано ниже).

Имея передаточную функцию системы и 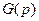, просто найти уравнение системы в операторной форме, т.е. 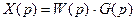и, используя обратное преобразование Лапласа, определить процесс управления 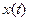. Такой путь значительно упрощает составление и решение уравнений систем автоматического управления.

Рассмотрим без доказательства некоторые свойства передаточных функций систем автоматического управления.

1. Передаточная функция 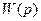является дробно-рациональной функцией от параметра p вида (5.1). Порядок числителя m равен порядку знаменателя n или меньше его.

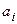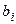2. Коэффициенты и передаточной функции есть вещественные числа, поскольку они определяются параметрами системы, которые всегда вещественны.

Как уже отмечалось ранее, воздействия, приложенные к САУ, делятся на задающие (управляющие) и возмущающие. При этом различают три вида передаточных функций замкнутых систем.

А. Передаточной функцией замкнутой системы по задающему (управляющему) воздействию 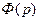называется отношение преобразования по Лапласу выходной величины 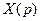к преобразованию по Лапласу задающего (управляющего) воздействия 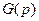при нулевых начальных условиях, т.е.

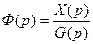, (4.2)

где ;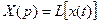

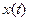- выходная величина;

;

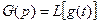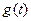– входная координата.

Б. Передаточной функцией замкнутой системы по возмущающему воздействию 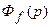называется отношение преобразования по Лапласу выходной величины 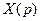к преобразованию по Лапласу возмущающего воздействия 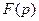при нулевых начальных условиях, т.е.

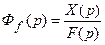, (4.3)

где ;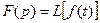

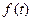- возмущающее воздействие.

В. Передаточной функцией ошибки замкнутой системы 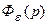называется отношение изображения по Лапласу сигнала ошибки 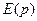к изображению по Лапласу задающего воздействия при нулевых начальных условиях 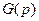, т.е.

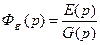, (4.4)

где ;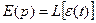

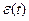- сигнал ошибки САУ.

В некоторых случаях при анализе и синтезе САУ бывает удобно вычислить передаточные функции замкнутой САУ через передаточные функции разомкнутой системы, которые определяются, если реально или мысленно разомкнуть цепь главной обратной связи в системе. При этом различают два вида передаточных функций разомкнутой САУ: по задающему воздействию и передаточную функцию разомкнутой САУ по возмущающему воздействию, которые соответственно обозначаются 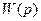и .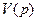

1. Передаточной функцией разомкнутой САУ по задающему воздействию 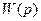называется отношение изображения по Лапласу выходной величины 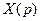разомкнутой САУ к изображению по Лапласу задающего воздействия 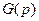при нулевых начальных условиях, т.е.

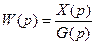, (4.5)

где ;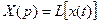

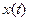- выходная величина разомкнутой САУ.

2. Передаточной функцией разомкнутой САУ по возмущающему воздействию 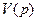называется отношение изображения по Лапласу выходной величины 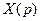разомкнутой САУ к изображению по Лапласу возмущающего воздействия 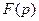при нулевых начальных условиях, т.е.

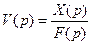. (4.6)