Функция V называется знакоопределенной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.
Абсолютная устойчивость нелинейных СУ
1. Понятие абсолютной устойчивости нелинейных СУ
Пусть дифференциальные уравнения нелинейной САУ заданы в виде системы уравнений первого порядка и записаны эти уравнения для переходного процесса в отклонениях всех переменных от их значений в установившемся режиме при постоянных внешних воздействиях. Эти уравнения для нелинейной системы n-го порядка будут иметь вид:
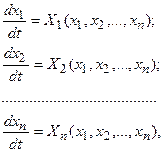 (25.1)
(25.1)
где 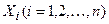 – функции произвольные и содержат любого вида нелинейности, но всегда удовлетворяют условию:
– функции произвольные и содержат любого вида нелинейности, но всегда удовлетворяют условию:
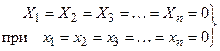 , (25.2)
, (25.2)
поскольку в установившемся режиме все отклонения переменных и их производные равны нулю по самому определению понятия этих отклонений.
Рассмотрим понятия о знакоопределенных, знакопостояных и знакопеременных функциях.
Пусть имеем функцию нескольких переменных
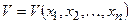 ,
,
Представим себе n-мерное пространство, в котором являются прямоугольными координатами. Тогда в каждой точке этого фазового пространства функция V будет называться знакоопределенной в некоторой области, если она во всех точках этой области вокруг начала координат сохраняет один и тот же знак и нигде не обращается в нуль, кроме только самого начала координат.
Функция V называется знакоопределенной, если она сохраняет один и тот же знак, но может обращаться в нуль не только в начале координат, но и в других точках данной области.
Функция V называется знакопеременной, если она в данной области вокруг начала координат может иметь разные знаки.
Рассмотрим теперь функцию Ляпунова и ее производную по времени.
Любую функцию
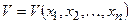 , (25.3)
, (25.3)
тождественно обращающуюся в нуль при 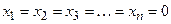 , называют функцией Ляпунова, если в ней в качестве величин
, называют функцией Ляпунова, если в ней в качестве величин 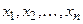 взяты отклонения переменных системы регулирования в переходном процессе, то есть
взяты отклонения переменных системы регулирования в переходном процессе, то есть
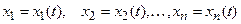 .
.
Производная от функции Ляпунова (25.3) по времени будет равна
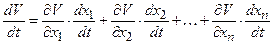 .
.
Подставив сюда значения 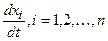 из уравнения (25.1), получим
из уравнения (25.1), получим
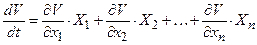 . (25.4)
. (25.4)
Таким образом, производная от функции Ляпунова по времени, так же как и сама функция Ляпунова, является некоторой функцией отклонений, то есть
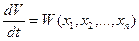 , (25.5)
, (25.5)
причем согласно свойству (25.2) эта функция W, так же как и сама V, тождественно обращается в нуль при 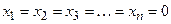 . Поэтому к ней в одинаковой степени можно применять все те же понятия знакоопределенности некоторой области вокруг начала координат, о которых говорилось выше по отношению к функции V.
. Поэтому к ней в одинаковой степени можно применять все те же понятия знакоопределенности некоторой области вокруг начала координат, о которых говорилось выше по отношению к функции V.
Учитывая сказанное выше, дадим общую формулировку теоремы Ляпунова об устойчивости и неустойчивости нелинейных систем и покажем их справедливость.
Формулировка теоремы Ляпунова об устойчивости нелинейных систем: если при заданных в форме (25.1) уравнениях системы n-го порядка можно подобрать такую знакоопределенную функцию Ляпунова 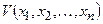 , чтобы ее производная по времени
, чтобы ее производная по времени 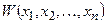 тоже была знакоопределенной (или знакопостоянной), но имела знак, противоположный знаку V, то данная система устойчива.
тоже была знакоопределенной (или знакопостоянной), но имела знак, противоположный знаку V, то данная система устойчива.
При знакоопределенной функции W будет иметь место асимптотическая устойчивость.
Покажем справедливость этой теоремы на простом примере системы третьего порядка (n=3).
Уравнения (25.1) для этой системы будут иметь вид:
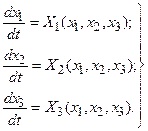 (25.6)
(25.6)
Возьмем знакоопределенную положительную функцию Ляпунова в виде
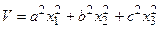 , (25.7)
, (25.7)
где a, b, c – произвольно заданные вещественные числа.
Будем придавать величине V возрастающие постоянные значения: V=0, С1, С2, С3,…, что означает:
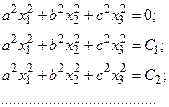
Первое из этих выражений соответствует одной точке 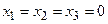 (началу координат фазового пространства), а остальные – поверхностям эллипсоидов в фазовом пространстве, причем каждый последующий эллипсоид содержит внутри себя целиком предыдущий.
(началу координат фазового пространства), а остальные – поверхностям эллипсоидов в фазовом пространстве, причем каждый последующий эллипсоид содержит внутри себя целиком предыдущий.
Возьмем, используя уравнение (25.5), производную от функции Ляпунова по времени, то есть
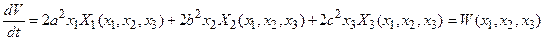 ,
,
где функции Х1, Х2, Х3взяты из (25.6).
Если полученная таким путем функция W(х1, х2, х3) окажется знакоопределенной отрицательной, то есть если
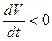 (25.8)
(25.8)
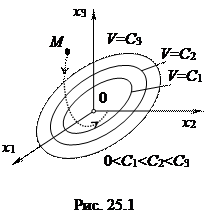 во всех точках исследуемого фазового пространства, кроме одного только начала координат, где
во всех точках исследуемого фазового пространства, кроме одного только начала координат, где 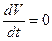 и х1=х2=х3=0, то при любых начальных условиях изображающая точка М (рис.25.1) вследствие (25.8) будет двигаться в сторону уменьшения значения V, т.е. будет пересекать эллипсоиды извне во внутрь и в направлении к началу координат, где V=0.
и х1=х2=х3=0, то при любых начальных условиях изображающая точка М (рис.25.1) вследствие (25.8) будет двигаться в сторону уменьшения значения V, т.е. будет пересекать эллипсоиды извне во внутрь и в направлении к началу координат, где V=0.
Это и означает затухание всех отклонений х1=х2=х3 в переходном процессе с течением времени, а это определяет устойчивость систем.
Если же функция W будет не знакоопределенной, а знакопостоянной, то, очевидно, траектория изображающей точки М не везде будет пересекать поверхность V=Ci, а может касаться их. В тех точках, где W
обращается в нуль (помимо начала координат), при этом необходимо выяснить – не “застрянет” ли изображающая точка там, где W=0.
2. Частотный метод исследования абсолютной устойчивости нелинейной СУ
Большие возможности для исследования устойчивости и даже качества нелинейных систем открывает предложенный в 1960 году румынским ученым В.М.Поповым критерий абсолютной устойчивости, особенно его геометрическая трактовка, позволяющая привлечь к исследованию рассматриваемого класса нелинейных систем частотные методы.
Под абсолютной устойчивостью понимают устойчивость в целом при любых начальных отклонениях для любой формы нелинейной характеристики, принадлежащей к некоторому определенному классу.
При наличии в системе одной нелинейности ее можно представить в виде структурной схемы, изображенной на рис. 25.2,а, а уравнение САУ записать:
для нелинейной части САУ
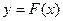 ; (25.9)
; (25.9)
для линейной части САУ
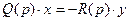 , (25.10)
, (25.10)
где
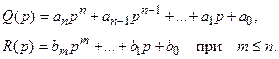
Пусть нелинейность 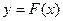 имеет любое очертание, не выходящее за пределы заданного угла arctg k ,то есть при любом х
имеет любое очертание, не выходящее за пределы заданного угла arctg k ,то есть при любом х
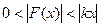 . (25.11)
. (25.11)
Пусть характеристическое уравнение линейной части системы имеет все левые корни или же, кроме них, имеется еще не более двух нулевых корней (допускается, чтобы 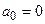 или
или 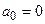 и
и 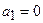 ). Следовательно, передаточная функция
). Следовательно, передаточная функция 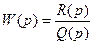 имела бы не более двух нулевых полюсов.
имела бы не более двух нулевых полюсов.
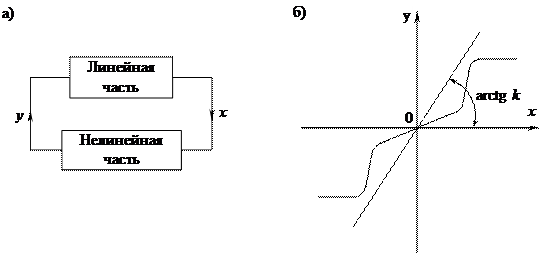 |
Рис. 25.2. Структурная схема приведенной нелинейной САУ
Формулировка теоремы В.М.Попова: для того чтобы нелинейная САУ была устойчивой, достаточно подобрать такое конечное действительное число h, при котором при всех w³0
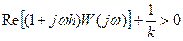 , (25.12)
, (25.12)
где W(jw) – амплитудно-фазовая частотная характеристика линейной части системы.
При наличии одного нулевого полюса требуется еще, чтобы
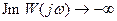 при w=0,
при w=0,
а при двух нулевых полюсах
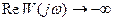 при w®0 и
при w®0 и 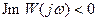 при малых w.
при малых w.
Другая формулировка той же теоремы, дающая удобную графическую интерпретацию, связана с введением видоизмененной частотной характеристики 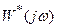 , которая определяется как
, которая определяется как
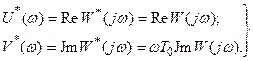 (25.13)
(25.13)
где T0 = 1c – нормирующий множитель.
График W*(jw) имеет вид (рис.25.3,а), аналогичный W(jw), когда в выражениях Q(p) и R(p) разность степеней (n-m)>1.
Если же разность степеней (n-m)=1, то конец графика W*(jw) будет на мнимой оси ниже начала координат (рис.25.3,б).
Преобразуем левую часть неравенства (25.12):
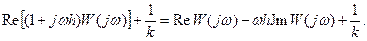
Положив 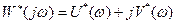 и используя соотношение (25.13), получим новое соотношение
и используя соотношение (25.13), получим новое соотношение
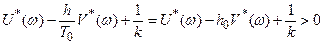 (25.14)
(25.14)
при всех w>0.
 |
Рис. 25.3. К определению устойчивости САУ методом В.М.Попова
Очевидно, что равенство
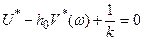 (25.15)
(25.15)
представляет уравнение прямой на плоскости W*(jw).
Отсюда вытекает следующая графическая интерпретация теоремы В.М.Попова: для того чтобы нелинейная система была устойчивой, достаточно подобрать такую прямую на плоскости W*(jw), проходящую через точку 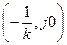 , чтобы вся кривая W*(jw) лежала справа от этой прямой.
, чтобы вся кривая W*(jw) лежала справа от этой прямой.
Между критерием абсолютной устойчивости В.М.Попова и вторым методом А.М.Ляпунова существует глубокая связь. В.А.Якубовичем было доказано в 1962 году, что, если выполняются условия абсолютной устойчивости В.М.Попова, то существует типовая функция А.М.Ляпунова – квадратичная форма плюс нелинейность.
3. Качество нелинейных систем
 Рассмотрим симметричные относительно оси времени колебательные процессы в нелинейной системе, которые приближенно могут быть описаны затухающей или расходящейся синусоидой с медленно меняющимися во времени показателями затухания и частотой.
Рассмотрим симметричные относительно оси времени колебательные процессы в нелинейной системе, которые приближенно могут быть описаны затухающей или расходящейся синусоидой с медленно меняющимися во времени показателями затухания и частотой.
Рис. 25.4
Для линейных систем, когда показатель затухания 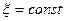 и частота
и частота 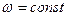 можно записать
можно записать 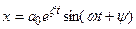 .
.
Если же частота 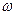 и показатель затухания
и показатель затухания 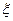 в процессе колебаний меняются, то это выражение должно записываться в другом виде
в процессе колебаний меняются, то это выражение должно записываться в другом виде
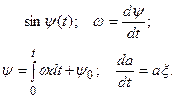
Таким образом, для нелинейной системы в первом приближении можно полагать
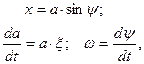
причем искомыми неизвестными будем считать медленно меняющиеся величины 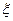 и
и 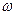 .
.
Диаграмма качества затухания симметричных нелинейных колебаний представляет собой семейство линий 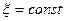 и линий
и линий 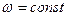 на плоскости с координатами k, a, причем k обозначает какой-либо из основных подлежащих выбору параметров системы (коэффициент усиления или др.).
на плоскости с координатами k, a, причем k обозначает какой-либо из основных подлежащих выбору параметров системы (коэффициент усиления или др.).
Для линейных систем линии 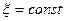 и
и 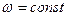 в тех же координатах имели бы вид вертикальных прямых, так как показатель затухания и частота колебательных переходных процессов в линейной системе не зависят от величины амплитуды колебаний a, а меняются только с изменением параметров системы (в данном случае k). В нелинейных же системах эти линии искривляются в зависимости от формы нелинейности и от общей структуры системы.
в тех же координатах имели бы вид вертикальных прямых, так как показатель затухания и частота колебательных переходных процессов в линейной системе не зависят от величины амплитуды колебаний a, а меняются только с изменением параметров системы (в данном случае k). В нелинейных же системах эти линии искривляются в зависимости от формы нелинейности и от общей структуры системы.
 |
Рис. 25.5
| <== предыдущая лекция | | | следующая лекция ==> |
| Метод гармонического баланса | | | Модели и характеристики случайных сигналов |
Дата добавления: 2015-12-11; просмотров: 2782;
