Метод гармонического баланса

1. Условия гармонического баланса и эквивалентная передаточная функция нелинейного элемента

Частотные методы, получившие широкое распространение при анализе и синтезе линейных систем, имеют ряд преимуществ перед другими методами исследований. Это, во-первых, простота составления и преобразования структурных схем и передаточных функций, во-вторых, удобство и большая наглядность расчетов с помощью частотных характеристик.

Поэтому естественным было желание использовать эти методы при исследовании нелинейных систем. Это оказалось возможным на основе гармонической линеаризации характеристик нелинейных звеньев системы автоматического регулирования.

Основы метода гармонической линеаризации или метода гармонического баланса были изложены в работах советских ученых Н.М. Крылова и Н.Н. Боголюбова в 1934 и 1937 годах. В дальнейшем идея этого метода применительно к системам автоматического регулирования бала развита Е.П. Поповым и Л.С. Гольдфарбом.

Этот метод позволяем исследовать устойчивость нелинейных систем с определением параметров (амплитуда, частота) возможных автоколебаний, производить выбор корректирующих цепей, обеспечивающих задание характеристики.

При гармонической линеаризации полагают выполнение следующих условий:

1. замкнутая нелинейная система представляется в виде двух частей – линейной и нелинейной (рис. 24.1);

2. линейная часть САУ является фильтром низких частот и чем выше фильтрующие свойства части, тем меньше погрешность линеаризации;

3. в нелинейной САУ предполагается гармонический характер колебаний.

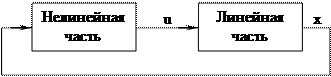Рис. 24.1. Схема нелинейной системы

Основная идея метода гармонической линеаризации заключается в следующем. Система автоматического регулирования представляется в виде двух частей – линейной и нелинейной (см. рис. 24.1). Пусть передаточная функция линейной части равна 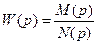, и уравнение линейной части имеет следующий вид:

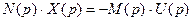. (24.1)

Далее, пусть выходной и входной сигналы нелинейной части связаны следующей зависимостью:

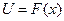, (24.2)

где 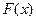- заданная нелинейная функция.

В выражении (24.2) для простоты показано, что выходная координата нелинейного звена зависит только от величины входного сигнала и не зависит от ее производных или интегралов, хотя рассматриваемый метод применим к более сложным нелинейным зависимостям, а также к системам с несколькими нелинейными звеньями.

Ставится задача отыскания параметров автоколебаний нелинейной системы. Автоколебания в нелинейной системе предполагаются синусоидальными, хотя эти колебания и имеют нелинейный характер. Однако ошибка такого предположения, как уже отмечалось, будет незначительной, так как линейная часть системы, являющаяся фильтром низких частот, подавляет колебания с высокими частотами. Поэтому будем отыскивать автоколебания системы в виде гармонических колебаний:

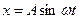. (24.3)

При входном синусоидальном сигнале на выходе нелинейного звена появляются некоторые периодические колебания. Их можно представить в виде бесконечного ряда гармонических составляющих:

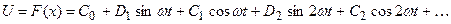, (24.4)

где 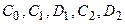- коэффициенты ряда Фурье.

В дальнейшем для упрощения считаем, что постоянная составляющая на выходе нелинейного звена отсутствует. Это значит, что нелинейная характеристика симметрична относительно начала координат и входное воздействие не содержит постоянной составляющей. Учитывая фильтрующие свойства линейной части, можно пренебречь всеми высшими гармоническими составляющими ряда Фурье. Поэтому приближенно выходной сигнал нелинейного элемента можно выразить через первую гармонику ряда (24.4):

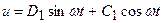. (24.5)

Из (24.3) находим

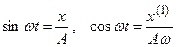. (24.6)

Подставив (24.6) в (24.5), получаем

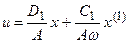. (24.7)

Если обозначить

,

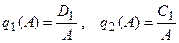то тогда будут справедливы следующие выражения:

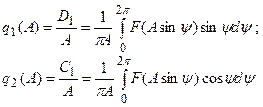
где .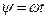

Уравнение (24.7) в операторной форме примет вид:

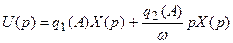. (24.8)

В результате проведенных преобразований исходное нелинейное уравнение (24.2) заменяется линеаризованным уравнением (24.8), коэффициенты которого зависят от амплитуды и частоты отыскиваемых автоколебаний.

Выражение для эквивалентной передаточной функции нелинейного элемента записывается так:

.

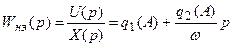Путем подстановки 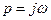переходим к эквивалентному коэффициенту передачи нелинейного элемента:

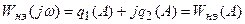, (24.9)

где 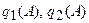называются коэффициентами гармонической линеаризации или гармоническими коэффициентами усиления.

Следует иметь в виду, что для однозначных характеристик нелинейных элементов .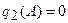

2. Исследование периодических режимов методом гармонического баланса

А. Определение параметров автоколебаний нелинейной системы методом Е.П.Попова

Для отыскания амплитуды и частоты возможных автоколебаний нелинейной системы можно воспользоваться условием выхода полученной линеаризованной системы на границу устойчивости по любому из известных критериев устойчивости. Е.П. Попов предложил использовать для этой цели критерий Михайлова.

Характеристическое уравнение замкнутой системы с учетом гармонической линеаризации нелинейного элемента можно записать так:

.

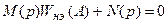Выражение для характеристического вектора Михайлова принимает вид:

.

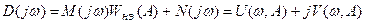Следует заметить, что амплитуда A и частота w автоколебаний входят как параметры в выражения для кривой Михайлова.

Для того чтобы система вышла на границу колебательности, кривая Михайлова должна пройти через начало координат (рис. 24.2).

Рис. 24.2. Кривая Михайлова (САУ на границе устойчивости)

Таким образом, амплитуда и частота периодических колебаний в нелинейной системе 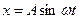могут быть определены при решении системы уравнений:

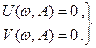(24.10)

Если при решении системы уравнений (24.10) полученные значения A и w вещественные и положительные, то это означает, что в исследуемой системе возможны автоколебания с найденными значениями параметров. В противном случае автоколебания в системе возникнуть не могут.

После того как параметры возможных автоколебаний будут определены, необходимо сделать проверку на устойчивость этого периодического решения, то есть необходимо выяснить, сводится переходный процесс к периодическим колебаниям или нет.

Автоколебания будут устойчивыми, если выполняется следующее условие:

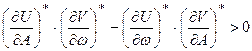. (24.11)

где звездочка означает, что частные производные вычисляются при подстановке параметров 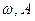проверяемого периодического решения. Если неравенство (24.11) не выполняется, то это соответствует неустойчивому периодическому решению. Условие (24.11) справедливо при исследовании систем до 4-го порядка включительно. Для систем более высокого порядка требуется просматривать ход всей кривой Михайлова.

При отсутствии автоколебательных режимов поведение исследуемой системы может быть самым различным. В настоящее время имеются приближенные способы определения переходного процесса в нелинейных системах при определенных входных воздействиях.

Б. Определение параметров автоколебаний нелинейной системы методом Л.С.Гольдфарба

Широкое применение получил графо-аналитический метод исследования нелинейной системы, предложенный Л.С. Гольдфарбом. Метод основан на использовании критерия устойчивости Найквиста. По критерию устойчивости Найквиста САУ будет находиться на границе устойчивости, если ее АФХ пройдет через точку 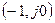, то есть 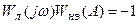. Отсюда

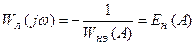, (24.12)

где 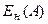- отрицательная обратная эквивалентная характеристика гармонически линеаризованного нелинейного звена.

Полученное условие позволяет определить параметры автоколебаний по точке пересечения АФХ линейной части САУ и обратной характеристики комплексной передаточной функции нелинейного элемента, взятой со знаком минус.

Рис. 24.3. К определению параметров автоколебаний методом Л.С. Гольдфарба

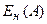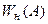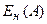Параметры автоколебаний определяют следующим образом. Сначала следует построить АФХ линейной части САУ (рис. 24.3) и заштриховать с левой стороны АФХ при изменении w от 0 до +¥. Затем построить характеристику нелинейного элемента . Для нелинейностей “ограничение”, ”нечувствительность” и релейная характеристика (идеальная) и вещественны, поэтому все возможные значения 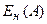и 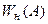находится на вещественной оси.

Если кривые не пересекаются, то решения уравнения (24.12) не существует и автоколебания невозможны. Если кривые пересекаются, то устойчивым автоколебаниям соответствуют те точки, в которых характеристика 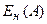пересекает амплитудно-фазовую характеристику 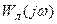, переходя из не заштрихованной области в заштрихованную (точка 2 на рис. 24.3). Частоту возможных автоколебаний определяют по АФХ линейной части 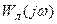, поскольку только линейная часть САУ зависит от частоты, а амплитуду колебаний определяют по характеристике нелинейного элемента, так как только эта характеристика зависит от амплитуды.

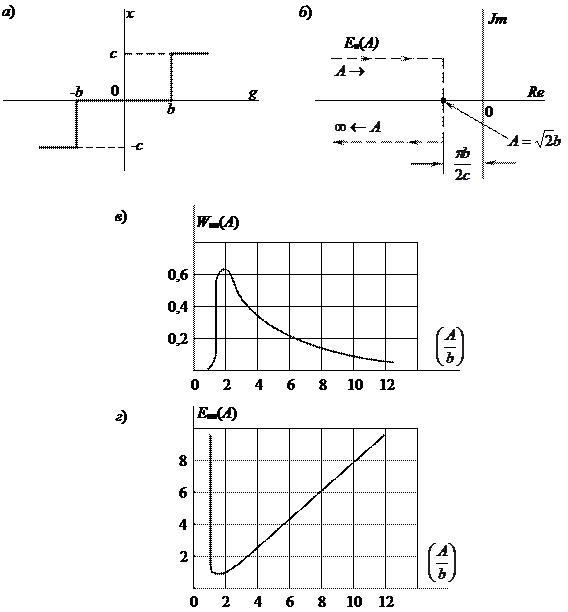Рис. 24.4. Релейная характеристика и график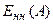и: и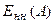

Для удобства определения амплитуды автоколебаний используют графики нормированных характеристик нелинейных элементов, зависящих от одного параметра. Так, для нелинейного элемента (рис. 24.4, а), имеющего 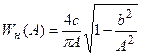, зависящую от трех параметров с, b, A, нормированную характеристику 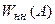, зависящую от одного параметра 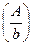, получают следующим образом:

.

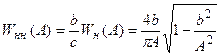Графики характеристик для рассматриваемого нелинейного элемента имеют вид, показанный на рис. 24.4, б, в, г.

Для определения амплитуды автоколебаний по величине 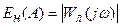находят 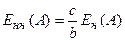. Используя характеристику 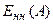, находят величину A. Например, для величины 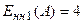(рис. 24.4, г) амплитуды возможных автоколебаний соответственно будут: 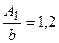; 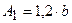, 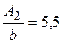; 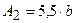, где b – величина зоны нечувствительности нелинейной характеристики (рис. 24.4, а).