Синтез корректирующих устройств

1. Основные этапы синтеза корректирующих устройств

При проектировании систем автоматического управления возника­ет необходимость в изменении динамических свойств систем с целью обеспечения требуемой устойчивости и точности управления. Это осу­ществляется путем определения синтеза и введения специальных кор­ректирующих звеньев. Эти звенья могут иметь различные передаточные функции и по-разному включаться в состав проектируемой системы.

По способу включения в схему системы (рис. 3.19) корректирую­щие устройства разделяются на следующие три типа:

1) последовательные корректирующие устройства;

2) параллельные корректирующие устройства;

3) корректирующие устройства в цепи местной обратной связи.

Обычно 2-й и 3-й типы корректирующих устройств объединяются в одну группу параллельных корректирующих устройств. На рис. 3.19 показаны:

W_c(р) - передаточная функция части исследуемой системы, непосредственно связанная с корректирующими звень­ями;

W_nз(р) - передаточная функция последовательного корректирую­щего звена;

W_П(р) - передаточная функция параллельного корректирующего звена;

W_oc(p) - передаточная функция корректирующего звена цепи обратной связи;

W₁(p) – передаточная функция исследуемой системы, не свя­занная с корректирующим устройством.

Свертывая структурные схемы, изображенные на рис. 3.19,а,б,в, получаем соответствующие эквивалентные передаточные функции части системы:

W_э1=W_c(p)·W_nз(р); (3.28)

W_э2=W_c(p)+ W_П(р); (3.29)

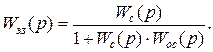(3.30)

В выражении (3.30) учитывается только отрицательная обратная связь.

Все рассмотренные типы корректирующих устройств имеют равные возможности воздействия на динамические характеристики системы. Однако из условия простоты технической реализации, надежности ис­полнения для конкретной проектируемой системы может отдаваться предпочтение одному из этих типов корректирующих устройств.

На основании равенства выражений для эквивалентных передаточ­ных функций (3.28), (3.29), (3.30) могут быть получены [1, 3] сле­дующие формулы перехода от одного типа корректирующего устройства к другому:

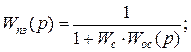(3.31)

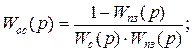(3.32)

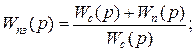(3.33)

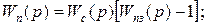(3.34)

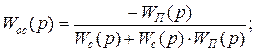(3.35)

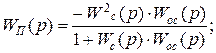(3.36)

Полученные зависимости показывают на функциональную связь пе­редаточных функций различных типов корректирующих устройств. Это означает, что заданная коррекция динамических характеристик синте­зируемой системы может быть принципиально осуществлена любым из рассмотренных типов корректирующих устройств.

Существует ряд способов синтеза корректирующих устройств мето­дом логарифмических частотных характеристик, которые отличаются в основном в построении желаемой ЛАЧХ. Этому вопросу посвящены рабо­ты В.В. Солодовникова, Т.Н. Соколова, А.Г. Ивахненко и др.

Синтез корректирующих устройств автоматического управления методом ЛАЧХ может быть разделен на ряд этапов.

1. С учетом требуемого коэффициента усиления разомкнутой си­стемы, выбранного из условия обеспечения допустимой ошибки в уста­новившемся режиме, строится логарифмическая амплитудно-частотная характеристика нескорректированной системы.

2. Строится желаемая ЛАЧХ, обеспечивающая требуемые показатели качества: перерегулирование s_max, время регулирования Т_max.

3. Определяется ЛАЧХ корректирующего устройства. Особенно про­сто это можно сделать для последовательного корректирующего уст­ройства, логарифмическая амплитудно-частотная характеристика кото­рого получается вычитанием ординат ЛАЧХ нескорректированной систем! из ординат желаемой ЛАЧХ.

4. Передаточная функция корректирующего устройства находится по его логарифмической амплитудно-частотной характеристике. После этого определяется принципиальная схема корректирующего устройства и вычисляются ее параметры. Затем вновь строится ЛАЧХ корректирую­щего устройства с учетом выбранной схемы и значений ее параметров.

5. Строится ЛАЧХ скорректированной системы и определяются показатели качества переходного процесса.

Построение делаемой ЛАЧХ является наиболее важным этапом рас­сматриваемой схемы синтеза корректирующего устройства.

2. Построение желаемой ЛАЧХ системы

Весьма существенным вопросом при синтезе корректирующих уст­ройств является определение оптимального вида переходного процесса. В качестве оптимального принимают монотонный переходный процесс с минимальным временем регулирования Т_min. При этом предполагают, что на вход системы подается ступенчатое воздействие.

Однако реализация корректирующего устройства, обеспечивающего оптимальный переходный процесс, может быть связана со значительными трудностями технического порядка. Кроме этого, может оказаться, что другие требования, например требование минимума статической погреш­ности, противоречат условиям обеспечения оптимального процесса. Поэ­тому синтезируемое корректирующее устройство должно компромиссно удовлетворять различным условиям, накладываемым на динамику регу­лирования с учетом возможностей технического исполнения. Таким обра­зом, желаемая логарифмическая амплитудно-частотная характеристика разомкнутой системы должна обеспечивать переходный процесс, близ­кий к оптимальному, и учитывать другие требования, предъявляемые к системе.

В.В. Солодовников предложил рассматривать три характерных уча­стка желаемой ЛАЧХ. Это участки характеристики, лежащие в области низких, средних и высоких частот.

1. Интервалнизких частот включает в себя частоты, меньшие первой сопрягающей частоты. Если эта частота больше единицы, то за верхний предел интервала низких частот принимается частота, равная единице,

2. Интервал средних частот включает в себя частоту срезаха­рактеристики.

3. Интервал высоких частот содержит лишь те сопрягающие часто­ты, пренебрежение которыми не оказывает существенного влияния на вид ЛАЧХ в интервале средних частот.

В[3] предлагается следующая методика построения желаемой ЛАЧХ по участкам:

1. Строится участок характеристики, лежащей в областинизкихчастот. Вид этого участка определяется порядком астатизма системы n и ее передаточным коэффициентом K. Это будет отрезок прямой с наклоном - n 20 дБ/дек, имеющий при частоте w = 1 ординату, рав­ную 20 lg k.

Для статической системы (n=0) этот участок должен иметь вид прямой, параллельной оси частоты и отстоящей от нее на величину 20lg k . Передаточный коэффициент системы k в этом случае выбира­ется из условия обеспечения требуемой статической погрешности.

2. Участок характеристики, лежащей в области средних частот, определяет в основном запас устойчивости системы и качество пере­ходного процесса при единичном ступенчатом воздействии.

Необходимо отметить, что любая типовая трапецеидальная вещест­венная частотная характеристика с точки зрения допустимого числа колебаний и перерегулирования может рассматриваться как желаемая частотная характеристика. Но техническая реализация соответствую­щего корректирующего устройства весьма затруднительна. Поэтому за желаемую вещественную частотную характеристику замкнутой систе­мы принимается типовая характеристика, состоящая из двух трапеций (рис. 3.37). Эта характеристика определяется такими параметрами:

1) интервалом положительности P(w) >0. Интервал положитель­ности характеризуется частотой 0 £ w £ w_п;

2) основным коэффициентом наклона æ= ;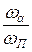

3) дополнительным коэффициентом наклона æ_d = ;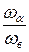

4) коэффициентом формы.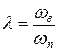

Обычно рассматривают такие вещественные частотные характери­стики, у которых основной коэффициент наклона лежит в пределах 0,2£æ£0,8. Для случая, когда основной коэффициент наклона близок к нулю, возникают технические трудности реализации соответст­вующего корректирующего устройства, а для характеристик с æ, близ­ким единице, запас устойчивости системы становится недостаточным.

Логарифмические амплитудно-частотные характеристики, соответ­ствующие типовым вещественным частотным характеристикам с 0,2£æ£0,8, в области средних частот имеют вид прямых, имею­щих наклон -20 ¸-30 дБ/дек. В случае, когда ЛАЧХ соответствует оптимальному переходному процессу, в области средних частот она имеет вид прямой с наклоном -20 дБ/дек.

Поэтому целесообразно для среднего интервала частот участок желаемой ЛАЧХ выбирать в виде прямой с наклоном -20 дБ/дек. Далее необходимо определить частоту среза желаемой ЛАЧХ.

Анализ ЛАЧХ, соответствующих типовым трапецеидальным вещест­венным характеристикам с различными параметрами, показывает, что частотаих среза определяется выражением

w_с=(0,6¸0,9)w_П. (3.37)

Зная w_П, можно определить частоту среза желаемой логарифмичес­кой амплитудной частотной характеристики (3.37).

Поэтому возникает задача вычисления w_П, и других параметров вещественной характеристики (рис. 3.21), которая определяет тре­буемые показатели качества переходного процесса. На рис. 3.22 по­казаны кривые, связывающие максимально допустимые значения пере­регулированияs_max и максимально допустимое время переходного процесса Т_max с максимальным значением типовой вещественной ча­стотной характеристики.

Эти зависимости s_max=f₁(p_max), Т_max=f₂(p_max) были по­строены на основе анализа кривых переходного процесса соответствующихим типовых вещественных характеристик. Кривые, показанные на рис. 3.22, получены для значений основного коэффициента наклона æ£0,8, дополнительного коэффициента наклона æ_а ≥ 0,4 и коэффициента формы l≥0,5.

Зависимость s_max=f(p_max) позволяет по максимально допустимому значению перерегулирования s_max определить максимальное -значение вещественной частотной характеристики p_max.

Кривая Т_max=f₂(p_max) дает возможность определить макси­мально допустимое время переходного процесса при заданных значе­ниях p_max и интервала положительностиw_П или, наоборот, ин­тервал положительности w_П по заданным значениям p_max и Т_max. Так как Т_max задается при синтезе, то порядок определения w_П сводится к следующему:

а) по кривой s_max=f₁(p_max) для требуемого значения s_max находится p_max;

б) по этому значению p_max используя кривую Т_max=f₂(p_max), определяем значение которое Т_max, в свою очередь, выражается таким образом:

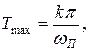(3.38)

откуда

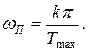(3.39)

Определив из (3.39) интервал положительности w_П, можно найти частоту среза w по равенству (3.37).

После этого через w=w_с проводится прямая с наклоном -20 дБ/дек.Таким образом, строится участок желаемой ЛАЧХ в интерва­ле средних частот.

На рис. 3.23 показаны графики, которые связывают максимально допустимую величину перерегулирования s_max с запасом устойчивости системы по амплитуде и фазе.

Эти графики построены на основании проведенных расчетов пере­ходных процессов для различных типовых трапецеидальных вещественных частотных характеристик. Используя эти зависимости (рис. 3.23), по заданному значению s_max определяется требуемый запас устойчи­вости по фазе и по амплитуде.

Запасы устойчивости системы по фазе и по амплитуде могут быть определены по-другому. Для этого по кривой s_max=f₁(p_max) (рис. 3.22) для заданного перерегулирования находится значение p_max. Обычно принимается, что

p_min=1- p_max.

Таким образом, находятся максимальное и минимальное значения вещественной частотной характеристики замкнутой системы, соответ­ствующие заданному перерегулированию s_max.

Например, дляs£30%находим p_max=1,2; p_min=- 0,2. Это означает, что ординаты вещественной частотной характеристики должны отвечать условию

1,2≥p(w)≥-0,2. (3.40)

Для того чтобы перейти к определению запасов устойчивости по ампли­туде и по фазе, на номограмме IX (рис. 3.14) строится прямоуголь­ник, охватывающий кривые p = 1,2 и p = -0,2.Логарифмическая ампли­тудно-фазовая характеристика разомкнутой системы для выполнения условия (3.40) не должна проходить через этот прямоугольник. А это соответствует выполнению следующих условий:

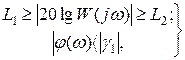(3.41)

где L₁ L₂ - ординаты верхней и нижнейсторон построенного прямо­угольника;

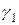- абсцисса боковой стороны прямоугольника.

Ординаты L₁ и L₂, полученные из условия обеспечения перере­гулирования не выше заданного s_max называют запасом устойчиво­сти по амплитуде, а 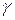= 180- 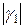- запасом устойчивости по фа­зе. Эти понятия отличаются от запасов устойчивости по фазе и по ам­плитуде, которые рассматриваются при анализе устойчивостисистемы.

3. Строится высокочастотная часть желаемой ЛАЧХ. Обычно уча­сток желаемой ЛАЧХ, расположенный в интервале высоких частот, сов­мещается с логарифмической амплитудной частотной характеристикой нескорректированной системы. Это объясняется тем, что в области вы­соких частот вид ЛАЧХ мало влияет на характер переходного процесса системы.

4. Отдельные участки желаемой ЛАЧХ сопрягаются между собой. Это сопряжение должно производиться таким образом, чтобы не умень­шились ранее найденные запасы устойчивости системы по фазе и по ам­плитуде. Кроме этого, при сопряжении участков желаемой ЛАЧХ обращается внимание на то, чтобы наклоны, желаемой характеристики были, возможно, более близки к наклонам ЛАЧХ нескорректированной части системы.

Это позволит получить более простую передаточную функцию кор­ректирующего устройства. Отдельные участки желаемой ЛАЧХ по возмож­ности должны сопрягаться отрезками прямых с наклонами, кратными ±20 дБ/дек.

3. Синтез последовательных корректирующих устройств

Для заданной системы автоматического регулирования с переда­точной функцией неизменяемой части W_H(p) требуется определить по­следовательное корректирующее устройство, обеспечивающее выполне­ние следующих требований:

1) система должна обладать астатизмом порядка n ;

2) величина передаточного коэффициента должна быть k;

3) перерегулирование переходной характеристики не должно пре­вышать s_max;

4) при числе колебаний не более n, время переходного процесса не должно превышать Т_max.

Рассмотрим структурную схему такой системы (рис. 3.24). Для передаточной функции такой системы в разомкнутом состоя­нии справедливо соотношение

W(p)=W_k(p)×W_H(p), (3.42)

где W_k(p)- передаточная функция последовательного корректирующего устройства;

W_H(p)- передаточная функция неизменной части системы автомати­ческого управления.

Амплитудно-фазовая характеристика разомкнутой системы равна

W(jw)=W_k(jw)×W_H(jw), (3.43)

где W_k(jw)=A_k(w) 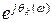- АФХ последовательного корректи­рующего устройства;

W_H(jw)=A_H(w) 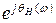- АФХ неизменной части системы.

Выражение (3.43) можно записать в виде

W(jw)=A(w)× ,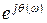

A(w)=A_k(w)×A_H(w),

q(w)=q_k(w)q_H(w).

В логарифмическом масштабе соотношение для амплитудно-частотных характеристик будет таким:

L(w)=20lgA(w)=20lg A_k(w)+20lg A_H(w)=L_k(w)+L_H(w). (3.45)

Логарифмическая амплитудно-частотная характеристика последовательного корректирующего устройства из выражения (3.45) находится вычитанном из желаемой логарифмической амплитудно-частотной характеристики системыL(w) логарифмической амплитудно-частотной характеристики неизменной части системы, т.е.

L_k(w)=L(w)-L_H(w). (3.46)

Далее, по L_k(w) находится передаточная функция корректирующе­го устройства, по которой определяются схема и значения параметров корректирующего звена.

Передаточную функцию последовательного корректирующего уст­ройства по L_k(w) находят следующим образом: определяют сопрягаю­щие частоты и по наклону характеристикиL_k(w) в точках сопряже­ния находят, какому типу звена соответствуетданный участок харак­теристики. По сопрягающим частотам вычисляются постоянные времени звеньев, а по расстоянию характеристики от оси частот определяется передаточный коэффициент корректирующего устройства.

Далее подбирается схематакого корректирующего устройства, которое имеет передаточную функцию, подобную найденной. По извест­ным коэффициентам передаточной функции вычисляются значения пара­метров выбранной схемы корректирующего устройства. В заключение производится проверка построением переходного процесса системы.