Правила вычисления неопределенного интеграла
Правила вычисления неопределенного интеграла получены и соответствуют правилам вычисления производной.
Мы помним, что производная суммы равна сумме производных дифференцируемых функций.
Теорема 1. Пусть 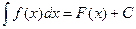 и
и 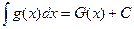 . Тогда справедлива формула
. Тогда справедлива формула 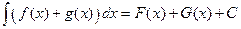 .
.
Доказательство сводится к проверке того, что производная правой части равна подынтегральной функции, что очевидно в силу условий теоремы.
Аналогично справедливы следующие теоремы:
Теорема 2. Пусть 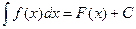 и
и 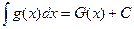 . Тогда справедлива формула
. Тогда справедлива формула 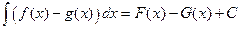 .
.
Теорема 3. Пусть 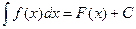 , тогда справедлива формула
, тогда справедлива формула 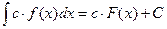 .
.
Итак, для дифференцируемых функций производная разности равна разности соответствующих производных и постоянный множитель выносится при вычислении интеграла.
Производная произведения дифференцируемых функций вычисляется по формуле 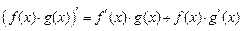 . Проинтегрировав обе части этого равенства, мы приходим к формуле интегрирования по частям в неопределенном интеграле.
. Проинтегрировав обе части этого равенства, мы приходим к формуле интегрирования по частям в неопределенном интеграле.
Теорема 4. Пусть существуют и интегрируемы функции 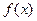 ,
, 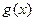 ,
, 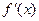 и
и 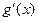 . Тогда справедлива формула
. Тогда справедлива формула 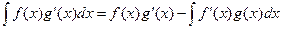 .
.
Для дифференцируемых функций 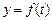 и
и 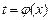 справедлива формула
справедлива формула 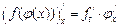 , т. е. производная сложной функции равна произведению соответствующих производных. Этой формуле соответствует формула замены переменных в неопределенном интеграле.
, т. е. производная сложной функции равна произведению соответствующих производных. Этой формуле соответствует формула замены переменных в неопределенном интеграле.
Теорема 5. Пусть существуют, дифференцируемы и интегрируемы функции 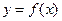 ,
, 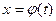 . Тогда справедлива формула
. Тогда справедлива формула 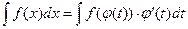 .
.
Дата добавления: 2015-12-10; просмотров: 500;
