Выпуклость и вогнутость графика функции, точки перегиба

Мы знаем геометрический смысл производной и тот факт, что у графика функции, имеющей производную, существует касательная к графику функции.

Определение 1. Функция 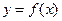называется выпуклой в точке 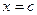, если в некоторой окрестности этой точки (точки графика функции с этой абсциссой), за исключением самой этой точки, касательная к графику функции 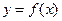лежит выше этого графика.

Определение 2. Функция 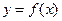называется вогнутой в точке 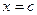, если в некоторой окрестности этой точки (точки графика функции с этой абсциссой), за исключением самой этой точки, касательная к графику функции 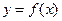лежит ниже этого графика.

Теорема 5. (Достаточные условия выпуклости и вогнутости) Пусть функция 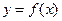имеет непрерывную вторую производную в окрестности точки 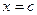. Тогда, если 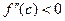, функция 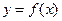является выпуклой в некоторой окрестности точки 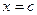. Если же 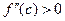, функция 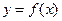является вогнутой в некоторой окрестности точки .

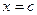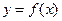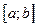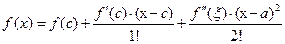Доказательство. Пусть функция непрерывна на отрезке . Запишем уравнение касательной Для доказательства теоремы применим формулу Тейлора с 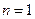. Мы видим, что взаимное расположение касательной и графиком функции определяется слагаемым 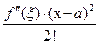, которое имеет тот же знак, что и знак второй производной в точке 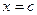. То есть при 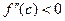касательная выше графика функции, при 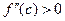касательная ниже графика функции. Теорема доказана.