Гармоники золотого ряда Фибоначчи

А теперь приступим к осмотру результатов конкретных исследований ряда Фибоначчи, полученных новым методом.

Ниже, на Рис.8 и 9, даны некоторые графические отображения данных расчёта различных цифровых «вмещений» и соответствующие этому абрисы вскрытых гармоник /по семействам/.

Абрисы и цифровые данные для 2-х и 3-х разрядных «вмещений» показаны выше, на Рис7.

ДругиеN-разрядные «вмещения» показаны ниже.

На Рис.8, даны числовые и графические формы 4-х разрядного «вмещения» для ряда Фибоначчи. Их условный индекс – F4.

В этом «семействе» гармоник имеется 4 реализации: F4(1), F4(2),F4(3), F4(41): 1578421….; 181818…; 248751…; 339669…;

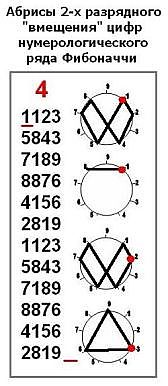
Рис.8

Кроме того, по абрисам реализаций видно, что здесь присутствует очень важная, но скрытая от непосредственного восприятия, закономерность алгоритма «Бабочки», которую мы уже выявляли другими способами в ряде работ [7-10].

А на следующих двух рисунках (Рис.9 и Рис.10) показаны гармоники, соответствующие 6-ти и 7-ми разрядным «вмещениям» (F6 и F7).

Здесь обнаруживается другая важная деталь: кроме простых (по виду абриса) гармоник (F6) могут существовать и сложные гармоники (F7).

Причём, для сложных гармоник имеют место случаи, когда все гармоники одного индекса, а здесь их 7 штук, имеют один и тот же абрис и различаются только точками начала считывания абрисов.

Рис.9

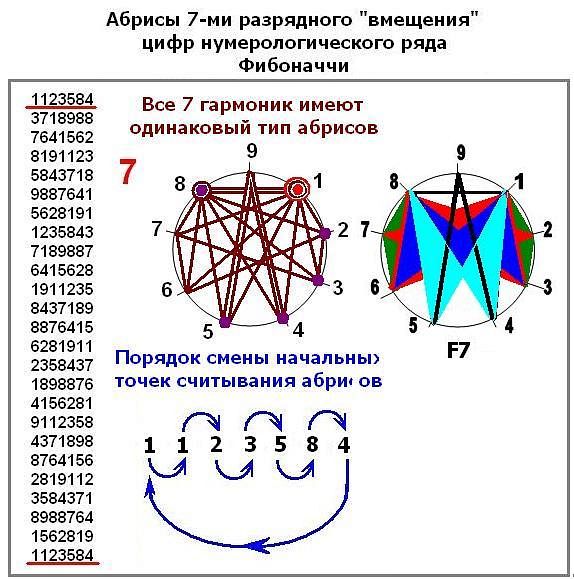
Рис.10

Случай F7 является аналогом реального физического явления. Такие спектральные гармоники анализируемых рядов подобны сложным радиосигналам.

Известно, что в радиоспектрах могут существовать полезные (модулирующие), но, тем не менее, зашифрованные сигналы.

И эти зашифрованные, сложные гармоники обычно подлежат дешифрированию теми же методами, которые привели к их выделению из сложно-модулированного несущего сигнала.

Совершенно так же можно поступить и с нашими сложными цифровыми гармониками.

Такой случай демонстрируется на примере F11 (Рис.11).

Рис.11

Можно заметить, что такое дополнительное «дешифрирование», применённое к первой гармонике индекса F11(1), выявило в ней наличие «субгармоники» вида F7 (см. выше, Рис.11 и отдельный Рис.12).

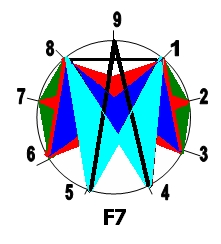
Рис.12

Из предварительного анализа, результаты которого отражены на Рис.11 и 12 разными цветами, можно видеть, что в этой гармонике (F7) «спрятан» целый набор элементарных гармоник, которые присутствуют в других спектральных гармониках.

Для данного случая – среди семейства гармоник ряда Фибоначчи (F6,F12), а также в гармониках ряда Люка (L3 и L6, см. Рис.13).

Рис.13

Тем самым, проявляется принципиальная возможность разложения сложных спектральных гармоник рядов на простые, элементарные формы гармоник.

Но, остаётся теоретический вопрос о том, как и почему эти элементарные (простые) гармоники так сказать «завязываются» в столь сложные узлы….

И это – тоже предмет дальнейших исследований.

Однако, вернёмся снова к нашим гармоникам.

Все вычисленные гармоники спектра ряда «Ф» (и расчёты) здесь приводить не имеет смысла. Для исследователей этого вопроса сделан дополнительный архив данных, который можно скачать по этой ссылке: http://www.numbernautics.ru/Archive/ZIP_F.zip

А общую картину спектра с найденными спектральными гармониками ряда Фибоначчи мы обязательно посмотрим (Рис.14).

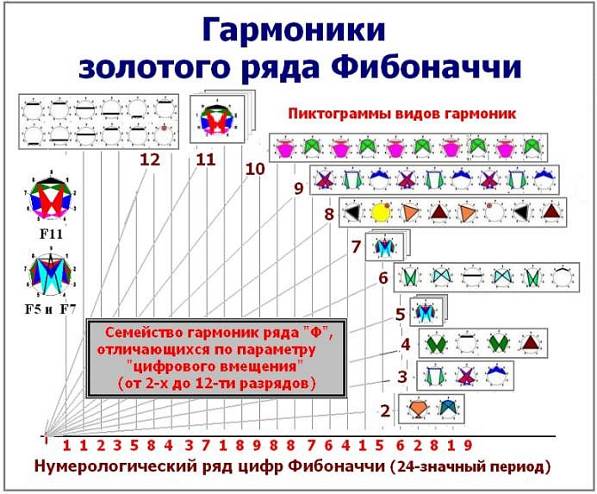
Рис.14