Всё познаётся в сравнении! Гармоники спектра рядаЛюка.

Была бы только «различимость» сопоставляемых объектов познания, как таковая, и метод … для того, чтобы что-либо сравнивать…

Теперь, для полноты первого знакомства с новым методом анализа рядов, нужно посмотреть действие этого метода ещё на каком-либо другом объекте.

Мне представляется интересным увидеть числовые спектры и гармоники другого «популярного» (у исследователей) золотого ряда, а именно – ряда Люка.

Полные расчётные данные по ряду Люка и картины абрисов его гармоник (для разных «вмещений») имеются в архиве – Архив иллюстраций

Сводная же картина результатов исследований по спектру ряда Люка и его гармоникам дана на Рис.19.

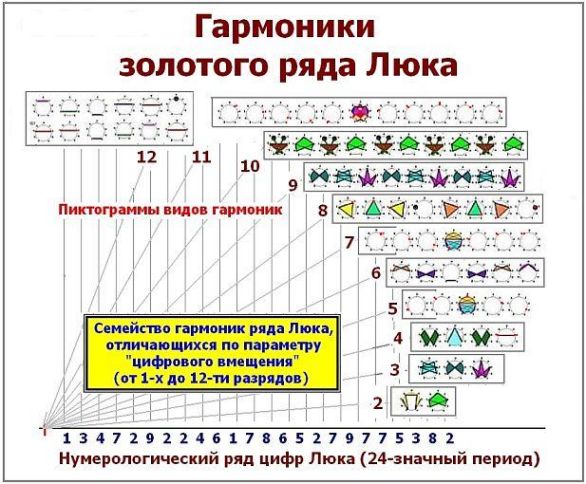
Рис.19

На этом рисунке мы снова видим другие (по своему виду) абрисы спектральных гармоник ряда. Снова, как и у ряда Фибоначчи, преобладают простые формы абрисов.

Однако, на позициях 5-ти, 7-ми и 11-ти - разрядных «вмещений», мы опять встречаем сложные гармоники. Как и для ряда Фибоначчи.

Этот факт свидетельствует, что «продольные» спектральные гармоники, полученные из цифр ряда Люка и взятые с промежутками в 5, 7 и 11 членов ряда, обладают некими особыми, достаточно специфическими свойствами, которые необходимо изучать дополнительно.

На этом, я полагаю, нужно закончить эту статью.

Продолжение следует...

Выводы:

Предложено новое понятие о продольном анализе числовых рядов, которое сопоставлено с традиционным, поперечным способом анализа тех же рядов.

Введено новое понятие о «гармонических числовых спектрах рядов», которое обосновывается и сопоставляется с аналогичными понятиями о физических спектрах и известными математическими понятиями, в том числе с понятием о «спектрах чисел».

Обсуждены особенности и специфики продольного и поперечного видов анализа числовых рядов.

С позиции динамики развития рядов акцентируется представление о том, что «продольные» закономерности (коды) анализируемых рядов являются своеобразными алгоритмами, определяющими структурные закономерности «поперечного» устроения этих рядов.

Высказано утверждение о том, что новый подход может повлечь за собой необходимость пересмотра наших представлений о многих понятиях. В частности, о понятии «числа».

Введено новое понятие о процедурах N-разрядных «вмещений», анализируемых рядов, лежащих в основе метода получения числовых спектров рядов.

Введено новое понятие об «элементарных цифровых формах», под которыми понимаются реальные и простые по своему виду гармоники рядов, разлагаемых в спектры.

Представлены практические результаты апробации нового метода в виде семейств гармоник спектров числовых рядов Фибоначчи, Люка и натурального ряда, а также соответствующие этому расчётные данные.

Показаны простые и надёжные возможности нового метода по идентификации получаемых семейств спектральных гармоник и отдельных гармоник внутри этих семейств.

Сделаны первые сопоставления гармоник новых спектров для трёх рядов и определены некоторые общие и различающие эти спектры признаки.

Показано, что доминирующее значение в спектрах имеют простые «цифровые формы» (гармоники), а также то, что сложные спектральные гармоники могут быть разложены в простые – тем же новым методом.

В рамках нового подхода высказана гипотеза о том, что числа ряда Фибоначчи можно трактовать, как некие особые «сгустки» более простых (элементарных) цифровых форм. И такие «сгустки» - продукт аддитивного «слияния» неких «продольно изменяющихся» (в одном направлении), элементарных цифровых форм, то есть гармоник исходного ряда Фибоначчи.

Сформулированы некоторые теоретические проблемы, лежащие в русле развития волнового подхода. В их числе вопросы порождения элементарных «цифровых форм», их агрегации и условий трансформации, порождающих систему различного вида, в частности, «золотых» (и иных «металлических») рядов.