Как будто простая задача

Самовар, вмещающий 30 стаканов, полон воды. Вы подставляете стакан под его кран и с часами в руках следите по секундной стрелке, во сколько времени стакан наполняется до краев. Допустим, что в полминуты. Теперь зададим вопрос: во сколько времени опорожнится весь самовар, если оставить кран открытым?

Казалось бы, здесь детски‑простая арифметическая задача: один стакан вытекает в 0,5 минуты, – значит, 30 стаканов выльются в 15 минут.

Но сделайте опыт. Окажется, что самовар опоражнивается не в четверть часа, как вы ожидали, а в полчаса.

В чем же дело? Ведь расчет так прост!

Прост, но неверен. Нельзя думать, что скорость истечения с начала до конца остается одна и та же. Когда первый стакан вытек из самовара, струя течет уже под меньшим давлением, так как уровень воды в самоваре понизился; понятно, что второй стакан наполнится в больший срок, чем в полминуты; третий вытечет еще ленивее, и т. д.

Скорость истечения всякой жидкости из отверстия в открытом сосуде находится в прямой зависимости от высоты столба жидкости, стоящего над отверстием. Гениальный Торичелли, ученик Галилея, первый указал на эту зависимость и выразил ее простой формулой:

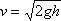
где v – скорость истечения, g – ускорение силы тяжести, a h – высота уровня жидкости над отверстием. Из этой формулы следует, что скорость вытекающей струи совершенно не зависит от плотности жидкости: легкий спирт и тяжеловесная ртуть при одинаковом уровне вытекают из отверстия одинаково быстро (рис. 56). Из формулы видно, что на Луне, где сила тяжести в 6 раз меньше, чем на Земле, потребовалось бы для наполнения стакана примерно в 2,5 раза больше времени, нежели на Земле.

Но возвратимся к нашей задаче. Если после истечения из самовара 20 стаканов уровень воды в нем (считая от отверстия крана) понизился в четыре раза, то 21‑й стакан наполнится вдвое медленнее, чем 1‑й. И если в дальнейшем уровень воды понизится в 9 раз, то для наполнения последних стаканов понадобится уже втрое больше времени, чем для наполнения первого. Все знают, как вяло вытекает вода из крана самовара, который уже почти опорожнен. Решая эту задачу приемами высшей математики, можно доказать, что время, нужное на полное опорожнение сосуда, в два раза больше срока, в течение которого вылился бы такой же объем жидкости при неизменном первоначальном уровне.

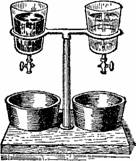
Рисунок 56. Что скорее выльется: ртуть или спирт? Уровень жидкости в сосудах одинаков.

Задача о бассейне

От сказанного один шаг к пресловутым задачам о бассейне, без которых не обходится ни один арифметический и алгебраический задачник. Всем памятны классически‑скучные, схоластические задачи вроде следующей:

«В бассейн проведены две трубы. Через одну первую пустой бассейн может наполниться в 5 часов; через одну вторую полный бассейн может опорожниться в 10 часов. Во сколько часов наполнится пустой бассейн, если открыть обе трубы сразу?»

Задачи этого рода имеют почтенную давность – без малого 20 веков, восходя к Герону Александрийскому. Вот одна из героновых задач, – не столь, правда, замысловатая, как ее потомки:

Четыре фонтана дано. Обширный дан водоем.

За сутки первый фонтан до краев его наполняет.

Два дня и две ночи второй над тем же должен работать.

Третий втрое, чем первый, слабей.

В четверо суток последний за ним поспевает.

Ответить мне, скоро ли будет он полон,

Если во время одно все их открыть?

Две тысячи лет решаются задачи о бассейнах и – такова сила рутины! – две тысячи лет решаются неправильно. Почему неправильно – вы поймете сами после того, что сейчас сказано было о вытекании воды. Как учат решать задачи о бассейнах? Первую, например, задачу решают так. В 1 час первая труба наливает 0,2 бассейна, вторая выливает 0,1 бассейна; значит, при действии обоих труб в бассейн ежечасно поступает 0,2 – 0,1 = 0,1 откуда для времени наполнения бассейна получается 10 часов. Это рассуждение неверно: если втекание воды можно считать происходящим под постоянным давлением и, следовательно, равномерным, то ее вытекание происходит при изменяющемся уровне и, значит, неравномерно. Из того, что второй трубой бассейн опоражнивается в 10 часов, вовсе не следует, что ежечасно вытекает 0,1 доля бассейна; школьный прием решения, как видим, ошибочен. Решить задачу правильно средствами элементарной математики нельзя, а потому задачам о бассейне (с вытекающей водой) вовсе не место в арифметических задачниках[38].

Рисунок 57. Задача о бассейне.

Удивительный сосуд

Возможно ли устроить такой сосуд, из которого вода вытекала бы все время равномерной струёй, не замедляя своего течения, несмотря на то, что уровень жидкости понижается? После того, что вы узнали из предыдущих статей, вы, вероятно, готовы счесть подобную задачу неразрешимой.

Между тем это вполне осуществимо. Банка, изображенная на рис. 58, – именно такой удивительный сосуд. Это обыкновенная банка с узким горлом, через пробку которой вдвинута стеклянная трубка. Если вы откроете кран C ниже конца трубки, то жидкость будет литься из него неослабевающей струёй до тех пор, пока уровень воды не опустится в сосуде до нижнего конца трубки. Вдвинув трубку почти до уровня крана, вы можете заставить всю жидкость, находящуюся выше уровня отверстия, вытечь равномерной, хотя и очень слабой струёй.

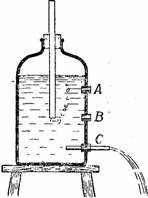
Рисунок 58. Устройство сосуда Мариотта. Из отверстия C вода течет равномерно.

Отчего это происходит? Проследите мысленно за тем, что совершается в сосуде при открытии крана C (рис. 58). Прежде всего выливается вода из стеклянной трубки; уровень жидкости внутри нее опускается до конца трубки. При дальнейшем вытекании опускается уже уровень воды в сосуде и через стеклянную трубку входит наружный воздух; он просачивается пузырьками через воду и собирается над ней в верхней части сосуда. Теперь на всем уровне B давление равно атмосферному. Значит, вода из крана C вытекает лишь под давлением слоя воды BC, потому что давление атмосферы изнутри и снаружи сосуда уравновешивается. А так как толщина слоя BC остается постоянной, то и неудивительно, что струя все время течет с одинаковой скоростью.

Попробуйте же теперь ответить на вопрос: как быстро будет вытекать вода, если вынуть пробочку B на уровне конца трубки?

Оказывается, что она вовсе не будет вытекать (разумеется, если отверстие настолько мало, что шириной его можно пренебречь; иначе вода будет вытекать под давлением тонкого слоя воды, толщиной в ширину отверстия). В самом деле, здесь изнутри и снаружи давление равно атмосферному, и ничто не побуждает воду вытекать.

А если бы вы вынули пробку A выше нижнего конца трубки, то не только вода не вытекала бы из сосуда, но в него еще входил бы наружный воздух. Почему? По весьма простой причине: внутри этой части сосуда давление воздуха меньше, чем атмосферное давление снаружи.

Этот сосуд со столь необычайными свойствами был придуман знаменитым физиком Мариоттом и назван по имени ученого «сосудом Мариотта».

Поклажа из воздуха

В середине XVII столетия жители города Рогенсбурга и съехавшиеся туда владетельные князья Германии во главе с императором были свидетелями поразительного зрелища: 16 лошадей изо всех сил старались разнять два приложенных друг к другу медных полушария. Что связывало их? «Ничто», – воздух. И тем не менее восемь лошадей, тянувших в одну сторону, и восемь, тянувших в другую, оказались не в силах их разъединить. Так бургомистр Отто фон Герике воочию показал всем, что воздух – вовсе не «ничто», что он имеет вес и давит со значительной силой на все земные предметы.

Опыт этот был произведен 8 мая 1654 г. при весьма торжественной обстановке. Ученый бургомистр сумел всех заинтересовать своими научными изысканиями, несмотря на то, что дело происходило в разгар политических неурядиц и опустошительных войн.

Описание знаменитого опыта с «магдебургскими полушариями» имеется в учебниках физики. Все же, я уверен, читатель с интересом выслушает этот рассказ из уст самого Герике, этого «германского Галилея», как иногда называют замечательного физика. Объемистая книга с описанием длинного ряда его опытов вышла на латинском языке в Амстердаме в 1672 г. и, подобно всем книгам этой эпохи, носила пространное заглавие. Вот оно:

ОТТО фон ГЕРИКЕ