Практические приемы оценки погрешности вычислений по квадратурным формулам.

Практическое применение полученных выше оценок погрешностей квадратурных формул связано с нахождением производных второго или даже четвертого порядка, что приводит к трудоемким вычислениям в тех случаях, когда подынтегральная функция f(х) задается сложным аналитическим выражением. Если же функция f(х) задана таблицей и ее аналитическое выражение неизвестно, то непосредственное использование этих оценок становится невозможным. С такими случаями обычно и приходится иметь дело при решении практических вычислительных задач.

Если таблица, которой задается подынтегральная функция f(х), содержит практически постоянные первые разности, т. е. f(х) ведет себя примерно как многочлен первой степени, то можно воспользоваться формулой трапеций.

Если же таблица функции f(х) содержит практически постоянные вторые или третьи разности, т. е. если f(х) ведет себя примерно как многочлен второй или третьей степени, то целесообразно использовать формулу Симпсона. Это, как уже отмечалось, связано с тем, что вычисление по формуле трапеций позволяет получить точное значение интеграла при условии линейности подынтегральной функции, а формула Симпсона в том случае, если подынтегральная функция является многочленом не выше третьей степени.

При табличном задании функции f(х) приближенное значение погрешности, получаемой при вычислении интеграла по той или иной квадратурной формуле, находится следующим образом:

1. Вычисление интеграла 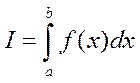выполняется два раза с шагами h и 2h. Полученные значения интеграла обозначаются соответственно S_h и S_2h.

2. Если предположить, что на рассматриваемом отрезке [а; b] вторая производная f"(x) изменяется медленно, то при вычислении интеграла по формуле трапеций можно воспользоваться следующим приближенным выражением для погрешности:

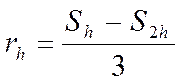(18)

3. В качестве исправленного (приближенного) значения интеграла можно взять следующее значение:

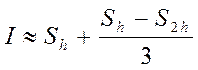(19)

4. Если предположить, что на рассматриваемом отрезке [а; b]четвертая производная f⁽⁴⁾(х) изменяется медленно, то при вычислении интеграла по формуле Симпсона можно считать, что погрешность приближенно равна

(20)

В качестве исправленного (приближенного) значения интеграла в этом случае можно взять:

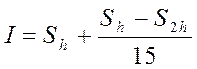(21)

В вычислительной практике часто пользуются также следующим правилом подсчета верных знаков в полученном результате: считают практически верными все совпадающие цифры значений S_h и S_2h.