Использование моделей

Модель вместо исходного объекта используется в случаях, когда эксперимент опасен, дорог, происходит в неудобном масштабе пространства и времени (долговременен, слишком кратковременен, протяжен…), невозможен, неповторим, ненагляден и т. д. Проиллюстрируем это:

«эксперимент опасен» — при деятельности в агрессивной среде вместо человека лучше использовать его макет; примером может служить луноход;

«дорог» — прежде чем использовать идею в реальной экономике страны, лучше опробовать её на математической или имитационной модели экономики, просчитав на ней все «за» и «против» и получив представление о возможных последствиях;

«долговременен» — изучить коррозию — процесс, происходящий десятилетия, — выгоднее и быстрее на модели;

«кратковременен» — изучать детали протекания процесса обработки металлов взрывом лучше на модели, поскольку такой процесс скоротечен во времени;

«протяжен в пространстве» — для изучения космогонических процессов удобны математические модели, поскольку реальные полёты к звёздам (пока) невозможны;

«микроскопичен» — для изучения взаимодействия атомов удобно воспользоваться их моделью;

«невозможен» — часто человек имеет дело с ситуацией, когда объекта нет, он ещё только проектируется. При проектировании важно не только представить себе будущий объект, но и испытать его виртуальный аналог до того, как дефекты проектирования проявятся в оригинале. Важно: моделирование теснейшим образом связано с проектированием. Обычно сначала проектируют систему, потом её испытывают, потом снова корректируют проект и снова испытывают, и так до тех пор, пока проект не станет удовлетворять предъявляемым к нему требованиям. Процесс «проектирование-моделирование» цикличен. При этом цикл имеет вид спирали — с каждым повтором проект становится все лучше, так как модель становится все более детальной, а уровень описания точнее;

«неповторим» — это достаточно редкий случай, когда эксперимент повторить нельзя; в такой ситуации модель — единственный способ изучения таких явлений. Пример — исторические процессы, — ведь повернуть историю вспять невозможно;

«ненагляден» — модель позволяет заглянуть в детали процесса, в его промежуточные стадии; при построении модели исследователь как бы вынужден описать причинно-следственные связи, позволяющие понять все в единстве, системе. Построение модели дисциплинирует мышление. Важно: модель играет системообразующую и смыслообразующую роль в научном познании, позволяет понять явление, структуру изучаемого объекта. Не построив модель, вряд ли удастся понять логику действия системы. Это означает, что модель позволяет разложить систему на элементы, связи, механизмы, требует объяснить действие системы, определить причины явлений, характер взаимодействия составляющих.

Свойства моделей

Свойства любой модели таковы:

- конечность: модель отображает оригинал лишь в конечном числе его отношений и, кроме того, ресурсы моделирования конечны;

- упрощенность: модель отображает только существенные стороны объекта;

- приблизительность: действительность отображается моделью грубо или приблизительно;

- адекватность: модель успешно описывает моделируемую систему;

- информативность: модель должна содержать достаточную информацию о системе - в рамках гипотез, принятых при построении модели.

Процесс моделирования есть процесс перехода из реальной области в виртуальную (модельную) посредством формализации, далее происходит изучение модели (собственно моделирование) и, наконец, интерпретация результатов как обратный переход из виртуальной области в реальную. Этот путь заменяет прямое исследование объекта в реальной области, то есть лобовое или интуитивное решение задачи. Итак, в самом простом случае технология моделирования подразумевает 3 этапа:

формализация,

собственно моделирование,

интерпретация.

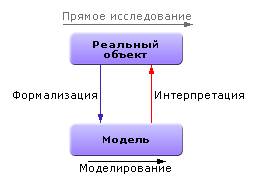
Рис. 1. Процесс моделирования (базовый вариант)

Если требуется уточнение, эти этапы повторяются вновь и вновь: формализация (проектирование), моделирование, интерпретация. Спираль! Вверх по кругу.

Поскольку моделирование — способ замещения реального объекта его аналогом, то возникает вопрос: насколько аналог должен соответствовать исходному объекту?

Вариант 1: соответствие — 100%. Очевидно, что точность решения в этом случае максимальна, а ущерб от применения модели минимален. Но затраты на построение такой модели бесконечно велики, так как объект повторяется во всех своих деталях; фактически, создаётся точно такой же объект путём копирования его до атомов (что само по себе не имеет смысла).

Вариант 2: соответствие — 0%. Модель совсем не похожа на реальный объект. Очевидно, что точность решения минимальна, а ущерб от применения модели максимален, бесконечен. Но затраты на построение такой модели нулевые.

Конечно, варианты 1 и 2 — это крайности. На самом деле модель создаётся из соображений компромисса между затратами на её построение и ущербом от неточности её применения. Это точка между двумя бесконечностями. То есть, моделируя, следует иметь в виду, что исследователь (моделировщик) должен стремиться к оптимуму суммарных затрат, включающих ущерб от применения и затраты на изготовление модели (см. рис. 2).

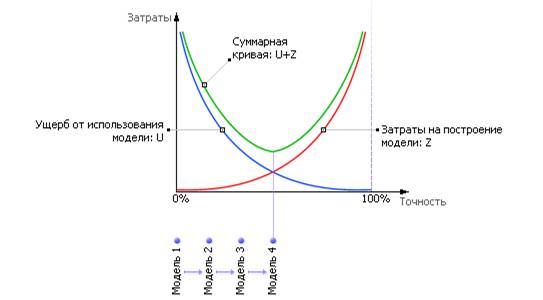
Рис. 2. Соотношение суммарных затрат и точности

для различных вариантов детализации прикладной модели

Просуммируйте две кривые затрат — получится одна кривая общих затрат. Найдите оптимум на суммарной кривой: он лежит между этими крайними вариантами. Видно, что неточные модели не нужны, но и абсолютная точность тоже не нужна, да и невозможна. Частое и распространённое заблуждение при построении моделей — требовать «как можно точнее».

«Модель — поиск конечного в бесконечном» — эта мысль принадлежит Д. И. Менделееву. Что отбрасывается, чтобы превратить бесконечное в конечное? В модель включаются только существенные аспекты, представляющие объект, и отбрасываются все остальные (бесконечное большинство). Существенный или несущественный аспект описания определяют согласно цели исследования. То есть каждая модель составляется с какой-то целью. Начиная моделирование, исследователь должен определить цель, отделив её от всех возможных других целей, число которых, по-видимому, бесконечно.

К сожалению, указанная на рис. 2 кривая является умозрительной и реально до начала моделирования построена быть не может. Поэтому на практике действуют таким образом: двигаются по шкале точности слева направо, то есть от простых моделей («Модель 1», «Модель 2»…) ко все более сложным («Модель 3», «Модель 4»…). А процесс моделирования имеет циклический спиралевидный характер: если построенная модель не удовлетворяет требованиям точности, то её детализируют, дорабатывают на следующем цикле (см. рис. 3).

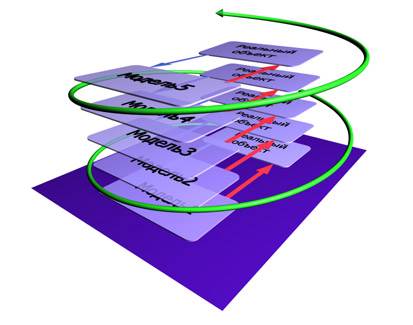
Рис. 3. Спиралевидный характер процесса проектирования и уточнения прикладных моделей

Улучшая модель, следят, чтобы эффект от усложнения модели превышал связанные с этим затраты. Как только исследователь замечает, что затраты на уточнение модели превышают эффект от точности при применении модели, следует остановиться, поскольку точка оптимума достигнута. Такой подход всегда гарантирует окупаемость вложений.

Из всего сказанного следует, что моделей может быть несколько: приближенная, более точная, ещё точнее и так далее. Модели как бы образуют ряд. Двигаясь от варианта к варианту, исследователь совершенствует модель. Для построения и совершенствования моделей необходима их преемственность, средства отслеживания версий и так далее, то есть моделирование требует инструмента и опирается на технологию.