Обратная интегральная функция распределения

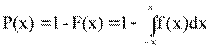
Функция интенсивности

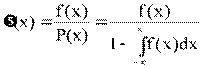
Закон распределения дискретной случайной величины задается в следующем виде:

Возможные значения	х₁	х₂	х₃		х_n
Вероятности	P₁	P₂	P₃		P_n

^ Вопрос 8. Основные характеристики, применяемые

Для описания случайных величин

Распределение случайных величин, изучаемых в теории надежности, характеризуют с помощью математического ожидания, дисперсии, среднего квадратичного отклонения и коэффициента вариации.

^ I. Непрерывные случайные величины:

Математическое ожидание М(t) характеризует среднее значение, вокруг которого группируются значения случайной величины.

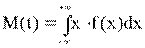
Для оценки разброса значений случайной величины около ее среднего значения применяются дисперсия и среднее квадратичное отклонение:

Дисперсия:

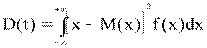
Среднее квадратичное отклонение:

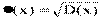
Чем больше разбросаны значения случайных величин, тем большими получаются значения дисперсии и среднего квадратичного отклонения.

Коэффициент вариации:

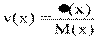
II. Дискретные случайные величины

Дата добавления: 2015-12-08; просмотров: 706;