Простейшие ЛЭ имеют следующие характеристики. 4 страница

Если в качестве исходного состояния вычитающего счетчика принять число 000, то состояние выходов триггеров счетчика отображают отрицательное число сосчитанных импульсов, представленное в дополнительном коде.

Литература:

1. В.В. Стрыгин «Основы вычислительной, микропроцессорной техники и программирования» стр: 97-102.

2. Э.В. Евреинов «Цифровая и вычислительная техника» стр: 122-125.

3. М. Димитрова «33 схемы на триггерах», стр: 47-50.

ЗАНЯТИЕ 1.1.7 Схемы и принцип действия различных типов счетчиков.

ВОПРОСЫ ЗАНЯТИЯ:

1. Схема и принцип действия суммирующего двоичного счетчика.

2. Схема и принцип действия вычитающего двоичного счетчика. Реверсивный счетчик.

3. Синхронные и асинхронные двоичные счетчики.

ПЕРВЫЙ ВОПРОС

Всуммирующем двоичном n-разрядном счетчике, состоящем из п тригге­ров, реализуется счетная последовательность чисел. Эта последовательность начинается с 0. Очередное число в этой последовательности получается прибавлением единицы к предыдущему числу. После того как последо­вательность доходит до максимального числа 2^п—1, она снова проходит через 0 и повторяется. В счетчике с п триггерами число возможных состояний равно 2ⁿ, мо­дуль счета К_стакже равен 2^п. Каждому состоянию счет­чика соответствует число в счетной последовательности от 0 до 2^п-1. Рассмотрим устройство двоичного 3-разряд­ного суммирующего счетчика. В таком счетчике можно реализовать счетную последовательность от 0 до 2³ – 1=7. Последовательность чисел может, быть задана совокупностью 3-разрядных двоичных чисел b₃ b₂b₁:000, 001, 010, 011, 100, 101, 110, 111.Поставим в соответствие каждому разряду b_iчисла выход триггера Q_i. В 3-раз­рядном счетчике с выходами Q₃Q₂Q₁ будет реализовываться счетная последовательность от 0 до 7.

Рис. 1

Триггеры Т изменяют свое состояние с окончанием входного сигнала, т.е. после перехода от уровня 1 к 0. Входной сигнал по шине С_о подается на счетный вход триггера 1. Работа счетчика может быть описана с помощью временной диаграммы (рис. 1б).

До начала прихода первого сигнала счетчик находил­ся в нулевом состоянии. Это соответствует наличию уров­ня 0 на выходах Q₁, Q₂, Q₃.С поступлением по шине С_о входных сигналов на счетный вход первого триггера на­чинается работа счетчика. С приходом первого сигна­ла триггер 1 переходит в состояние 1 и на его выходе устанавливается уровень Q = l. Поскольку на счетных входах триггеров 2 и 3 не происходит изменения уровня с 1 на 0, эти триггеры сохраняют состояния Q₂ = 0, Q₃=0. С приходом второго сигнала триггер 1 переходит в состояние 0. В момент изменения уровня на его выхо­де с Q₁=l на уровень Q₁ = 0 триггер 2 переходит в со­стояние 1 и на его выходе устанавливается уровень Q₂ = 1. Состояние триггера 3 остается неизменным. Триг­гер 3 перейдет в состояние 1 лишь при поступлении на счетный вход триггера 1 четвертого по счету сигнала. При этом триггер 1 перейдет из состояния 1 в состоя­ние 0. Переход от состояния 1 к состоянию 0 вызовет изменение уровней от 1 к 0 на счетном входе 2. В ре­зультате триггер 2 также перейдет из состояния 1 в со­стояние 0. Такой переход повлечет за собой изменение уровня от 1 к 0 на счетном входе 3. В результате на выходе Q₃ триггера 3 установится уровень 1. При этом на выходах Q₁ и Q₂ триггеров 1 и 2 будут уровни 0. Следо­вательно, в счетчике будет зафиксировано число 4 в дво­ичном представлении. Это соответствует фиксации мо­мента поступления четвертого сигнала.

К моменту прихода восьмого по счету сигнала на вы­ходах триггеров Q₁,Q₂, Q₃будет установлен уровень 1. Поступление восьмого сигнала на счетный вход тригге­ра 1 вызовет изменение его состояния с 1 на 0. В свою очередь, изменение состояния триггера 1 вызовет изме­нение состояния триггера 2, а изменение состояния триг­гера 2 приведет к изменению состояния триггера 3. В результате все триггеры счетчика перейдут в состоя­ние 0. Счетчик будет подготовлен.к счету новой последовательности из восьми сигналов.

Таблица 1.

Работу счетчика можно также представить как процесс суммирования предыдущего значения счетчика с единицей. Такое суммирование вы­полняется по обычным правилам выполнения операции сложения чисел в двоичной системе. При этом можно отметить следующие особенности:

1) Если в младшем разряде предыдущего значения счетчика имеется 0, то суммирование изменяет, лишь цифру младшего разряда на 1;

2) Если в т младших разрядах содержится 1, а в (m+1)-м разряде – 0, то цифры т младших разрядов изменяются на значение 0, а в (m+1)-м разряде – на значение 1.

ВТОРОЙ ВОПРОС

Ввычитающих счетчиках с приходом очередного счетного сигнала предыдущий результат уменьшается на едини­цу. В вычитающем двоичном n-разрядном счетчике реа­лизуется счетная последовательность чисел, начиная с 2^п – 1 и кончая 0. Очередное число в этой последова­тельности получается вычитанием единицы из предыду­щего числа. После получения значения 0 последователь­ность повторяется. Порядок смены состояний вычитаю­щего счетчика может быть описан табл. 2. Из таблицы следует еще одно отличие вычитающего счет­чика от суммирующего: триггер каждого последующего разряда переходит в другое состояние при сигнале зай­ма, обратном сигналу переноса в суммирующем счетчике.

Рис. 2

Функционирование i-гo разряда вычитающего счетчи­ка можно описать логическими выражениями переноса П_i+1 и разности c_iиз табл. 3. Таблица получается на основании анализа особенностей вычитания единицы из двоичного числа.

Таблица 3.

Для ускорения работы вычитающих двоичных счетчиков могут использоваться схемы с параллельным и параллельно-последовательным переносом.

В реверсивном счетчике объединяются схемы сумми­рующего и вычитающего счетчиков. Кроме того, сущест­вует возможность управления направлением счетчика, для чего предусматривается дополнительное КЦУ.

В реверсивном счетчике на Т-триггерах (рис. 3а) счетные сигналы поступают на вход Т-триггера через логические элементы в случае, если они открыты еди­ничными сигналами с выходов предыдущих разрядов. Для счетных сигналов предусмотрены два входа.

Рис. 3

На выхо­де < 0 сигнал появляется при заполнении счетчика ну­лями. Это сигнал займа в следующий счетчик в схеме вычитающего счетчика. Условное обозначение реверсив­ного счетчика с двумя входами приведено на рис. 3б. Если требуется построить реверсивный счетчик с одним источником сигналов для счета, то необходимо преду­смотреть специальное ПЦУ для переключения на сумми­рующий + 1 или вычитающий —1 входы.

Используя интегральные схемы 4-разрядных счетчи­ков с выходами займа и переноса, можно строить ревер­сивные счетчики большей разрядности. На рис. 4

при­веден пример построения 8-разрядного реверсивного счетчика из двух 4-разрядных.

Здесь допускается уста­новка заданного исходного состояния счетчика с помо­щью ввода в счетчик нужной кодовой комбинации a₀a₁...a₇ при наличии разрешения на входе записи С_зап.

Используя возможность посылки сигналов на вход «Уст. 1» или «Уст. О» в триггерах счетчика можно уста­новить состояния 0 или 1. При необходимости можно ис­пользовать выходы >15 первого или второго 4-разряд­ных счетчиков. Частота повторения сигналов на этих выходах в 16 или 256 раз меньше по сравнению с сиг­налами, поступающими на вход С_о.

ТРЕТИЙ ВОПРОС

Синхронные и асинхронные двоичные счетчики.Дво­ичные счетчики, состояние триггеров которых изменяет­ся одновременно под воздействием сигнала синхрониза­ции на входах всех триггеров, получили название син­хронных. Схема синхронного счетчика со сквозным пе­реносом на Т-триггерах приведена на рис. 5а, его условное обозначение дано на рис. 5б.

Рис. 5

Синхронные счетчики используются в синхронных цифровых системах. Последовательные цифровые устройства в этих системах обычно зависят друг от друга и управляются oт общего источника синхросигналов. В таких условиях нужно, чтобы все триггеры во всех ПЦУ изменяли свое состояние одновременно по сигналу синхронизации, чтобы текущее состояние триггеров ис­пользовалось для определения их следующего состоя­ния. Применяемая здесь схема со сквозным переносом легко наращивается простым добавлением схемы И с двумя входами. Однако для определения значения са­мого правого входа Т n-разрядного счетчика необходи­мо время, равное времени распространения сигнала че­рез одну схему И, умноженному на п—1.

Схема синхронного счетчика была исполь­зована при рассмотрении реверсивного счетчика (см. рис 3).

В асинхронных счетчиках синхронизирующие входы триггеров соединяются с входами соседних триггеров. Поэтому состояние триггера меняется в ответ на изме­нение состояния соседнего триггера, а не в ответ на воз­действие сигнала внешней синхронизации.

В асинхронных счетчиках волна изменений состояния распространяется по всей цепочке триггеров, в отличие от синхронных счетчиков, где происходит изменение со­стояния всех триггеров одновременно. Схема асинхрон­ного счетчика на D-триггерах с динамическим управле­нием приведена на рис. 6а, а его условное обозначе­ние— на рис. 6б. В триггерах с прямым динамичес­ким входом изменение состояния осуществляется при перепаде уровня от 0 к 1. В асинхронных счетчиках с последовательным переносом вход каждого последую­щего триггера соединяется с инверсным выходом преды­дущего. Сигналы счета поступают на вход С_о. С помо­щью сигнала, поступающего на вход «Уст. 0», счетчик может быть установлен в начальное состояние.

Асинхронные счетчики также были рассмотрены при описании суммирующих и вычитающих счетчиков. Асинхронные счетчики позволяют обес­печить большую скорость счета. Объясняется это тем, что после переключения первого триггера счетчика на него можно подавать следующий сигнал, не ожидая распространения воздействия от сигнала через весь счетчик.

В синхронном счетчике между сигналами на счетный вход должно проходить время, определяемое переключением одного триггера и установлением значе­ний на всех входах 7. С учетом сказанного можно отме­тить, что все типы суммирующих, вычитающих, ревер­сивных счетчиков могут быть реализованы в виде как синхронных, так и асинхронных счетчиков.

Литература:

1. Э.В. Евреинов «Цифровая и вычислительная техника». Москва, «Радио и связь», 1991. Стр: 123-133.

ЗАНЯТИЕ 1.1.8 Назначение схем коммутаторов. Логика работы коммутаторов. Типовые схемы коммутаторов. Назначение мультиплексоров и демультиплексоров, структурные схемы, принцип действия, области применения.

ЗАНЯТИЕ 1.1.9 Преобразование прямого кода в обратный. Преобразование прямого кода в дополнительный. Преобразование десятично-двоичного кода в двоичный и обратно. Назначение и принцип построения схем сравнения кодов.

ВОПРОСЫ ЗАНЯТИЯ:

1. Назначение, структурная схема и принцип действия мультиплексоров.

2. Назначение, структурная схема и принцип действия демультиплексоров.

3. Арифметические основы преобразования кодов в вычислительных устройствах. Назначение, структурная схема и работа преобразователей кодов.

ПЕРВЫЙ ВОПРОС

Мультиплексоры обеспечивают ком­мутацию на выходе одного из нескольких информацион­ных входных сигналов в соответствии с заданным кодом на управляющих входах. Иными словами мультиплексором называется комбинационное устройство, предназначенное для коммутации в желаемом порядке сигналов с нескольких входных шин на одну выходную. С помощью мультиплексора осу­ществляется временное разделение информации, поступающей по разным ка­налам. Его можно уподобить бесконтактному многопозиционному пере­ключателю.

Входы мультиплексора делятся на информационные, адресные и разреша­ющие (стробирующие). На информационные входы подается информация, передаваемая на выход мультиплексора. Адресные входы помогают выбрать нужный информационный вход, а на разрешающий вход подается стробирующий сигнал, разрешающий подключение выбранного входа на один общий (реже два взаимоинверсных) выход. Разрешающий вход, как правило, один, а число информационных и адресных входов взаимосвязано. Если число адресных входов n, то с их помощью можно коммутировать 2ⁿ каналов, т.е. число информационных входов 2ⁿ.

Наличие разрешающего входа позволяет синхронизировать работу мультиплексора с работой других узлов, а также наращивать его разряд­ность.

Условное графическое обозна­чение одного из вариантов мультиплексора представлено на рис. 1. В зависимости от комбинации сигналов уп­равления х₁,х₂.х₃ он обеспечивает коммутацию одного из восьми информационных входных сигналов D на выход у. Сигнал синхронизации V в данном случае имеет нулевое активное значение, разрешающее передачу информации с одного из входов на выход.

Структурная формула, оп­ределяющая функционирование рассматриваемого восьмивходового мультиплексора, имеет вид

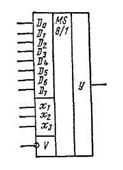
Рис. 1. Условное графическое обозна­чение мультиплексора.

Мультиплексор можно реализовать с помощью ЛЭза­данного базиса. В его структуру можно ввести и более сложные цифровые устройства. Сопоставляя формулы можно заметить, что для каждого входа D комбинации сигналов управления x₁,x₂,x₃в мультиплексо­ре такие же, как и в дешифраторе. Следовательно, составной частью мультиплексора является дешифратор. Структурная схема одного из возможных вариантов мультиплексора с четырьмя информационными входами D приведена на рис 2.

Рис. 2. Структурная схема мультиплексора с

четырьмя информационными входами.

ВТОРОЙ ВОПРОС

Демультиплексоры представляют собой цифровые устройства для коммутации информационного входного сигнала в одном из нескольких выходов в соответствии с заданным кодом на управляющих входах. Иными сло­вами, демультиплексоры решают задачи, обратные муль­типлексированию.

Условное графическое обозначение демультиплексора с четырьмя информационными выходами представлено на рис. 3.12.

В демультиплексорах сигналы с одного информацион­ного входа распределяются в необходимой последовательности по несколь­ким выходам соответствующим кодам на адресных входах. При п адресных входах демультиплексор может иметь до 2ⁿ выходов.

Рис. 3. Условное графическое обозначение демультиплексора.

Структурные формулы, опре­деляющие формирование выходных сигналов такого демультиплексора, имеют вид

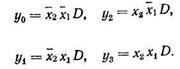
Именно такими выражениями определяется формирова­ние выходных сигналов дешифратора, использующего синхронизацию по входу D. Поэтому в качестве демультиплексора можно применять дешифратор, в котором ин­формационный входной сигнал подан на вход синхрони­зации. Примером является реализация 2-разрядного демультиплексора с нулевыми активными сигналами на основе рассмотренного ранее сдвоенного дешифратора

К155ИД4. Если первый разряд D_p1 подать на вход V₁, а второй разряд D_р2-на вход V₃, то в зависимости от комбинации значении x₁x₂ можно обес­печить коммутацию этого 2-разрядного кода D_plD_p2 на любой из четырех выходов у. На остальные входы синхро­низации V₂ и V₄ можно подать постоянные, значения (V₂=1, V₄=0) либо использовать их для организации синхронной передачи информации на выходы (рис. 4).

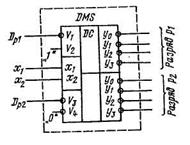
Рис. 4. Пример реализации 2-разрядного демультиплексора с нулевыми

активными сигналами на основе сдвоенного дешифратора К155ИД4.

ТРЕТИЙ ВОПРОС

Исходные данные, а также промежуточные результаты в ЭВМ могут быть положительными и отрицательными. Для изображения знака числа в разрядной сетке ЭВМ перед старшим цифровым раз­рядом вводится дополнительный знаковый разряд, в который для изображения положительного числа заносится нуль, а для изобра­жения отрицательного числа — единица. Для кодирования чисел в ЭВМ применяют специальные коды — прямой, обратный и до­полнительный.

Прямой код.Изображение двоичного числа X в прямом коде [Х]_пр основано на представлении его абсолютного значения с за­кодированным знаком.

В общем случае формула для образования прямого кода дроб­ного двоичного числа X имеет вид

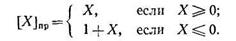
Прямой код [Х]_пр положительного числа X в закодированном виде полностью совпадает с записью самого числа: если Х=+0 .

Прямой код [Х]_пр отрицательного числа —X в закодированном виде имеет такую запись: если Х= -0. x₁x₂. . .х_т,то [X]_пр= 1. x₁x₂. . .х_т.

Пример.Представить числа Х= + 0 11010и Х= - 0.01010в прямом коде. Тогда

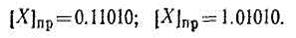
Прямой код используется в ЭВМ для хранения положительных и отрицательных чисел в запоминающих устройствах.

Обратный код.Для упрощения структуры машины отрицатель­ные дроби, представленные в двоичной системе счисления, кодиру­ются в виде дополнений до 2 или до 2 - 2^-т (т — количество раз­рядов, 2 — основание двоичной системы счисления). Код, образо­ванный дополнением до 2, называют дополнительным, а код, обра­зованный дополнением до 2 - 2^-т, - обратным. Обратный код числа X обозначается [Х]_обр.

Обратный код положительного числа совпадает с его прямым кодом: если Х>0, то [X]_o6р=lX]_np=X. Обратный код отрицатель­ного числа образуется следующим образом:

1) в знаковом разряде записывается единица;

2) в цифровых разрядах единицы заменяются нулями, а нули – единицами.

Так, обратный код положительного числа Х=+0.10110 равен этому числу [X]_о6р=0.10110, а обратный код отрицательного чис­ла Х= -0.01001 равен

[X]_о6р = 1.10110.

Таким образом, формула для образования обратного кода дроб­ного двоичного числа X имеет вид

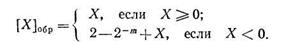
Специальные коды (обратный и дополнительный) позволяют опе­рацию вычитания в ЭВМ заменить операцией сложения, что дает возможность сведения всех арифметических операций к выполне­нию операции сложения.

Пример. Сложить числа Х=+0.101 и Y=-0.001 в обратных кодах:

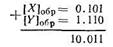
При сложении кодов единица старшего разряда вышла влево. В этом слу­чае для получения правильного результата необходимо выполнить операцию циклического переноса. Эта операция заключается в том, что единица, вы­шедшая за знаковый разряд, отбрасывается, а к младшему разряду числа прибавляется единица:

При этом результат операции сложения положительный, так как в знаковом разряде стоит 0.

Операция циклического переноса необходима только тогда, когда единица выходит за знаковый разряд. Если в знаковом разряде ре­зультата стоит 1, то результат операции сложения будет отрицатель­ным. При использовании целых чисел формула для образования обратного кода имеет вид

где п — число разрядов.

Дополнительный код. Дополнительный код положительного чис­ла совпадает с его прямым кодом, т. е. [Х]_доп=[Х]_пр=Х. Допол­нительный код отрицательного двоичного числа образуется следую­щим образом:

1) в знаковом разряде поставить единицу;

2) во всех цифровых разрядах заменить единицы нулями, а нули - единица­ми;

3) к младшему разряду числа прибавить единицу.

Так, дополнительный код положительного числа Х= +0.10010 равен этому числу, т. е. [Х]_доп=0.10010; дополнительный код от­рицательного числа

Х=-0.0110 будет [Х]_доп= 1.1001 +0.0001 = 1.1010 или отрицательного числа

X=-0.11001 будет [Х]_доп= 1.00110+0.00001 = 1.00111.

Таким образом, формула для образования дополнительного ко­да дробного двоичного числа имеет вид

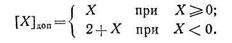
Аналогичным способом можно получить формулу для образования дополнительного кода целого двоичного числа:

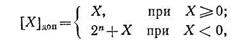
где п — число разрядов.

При сложении в дополнительном коде единица переноса, вышед­шая за знаковый разряд, отбрасывается и к младшему разряду чис­ла единица не прибавляется.

Точка в цифровых устройствах специально не изображается. Место, где должна находиться точка, определяется расположением цифр по отношению к воображаемой точке.

При сложении чисел в машине могут получиться числа, которые по абсолютной величине больше допустимого значения, что ведет к искажению результатов вычислений. Поэтому случаи переполнения разрядной сетки должны немедленно обнаруживаться. Для этого в машинах применяются специальные схемы, фиксирующие такие случаи и приостанавливающие решение. Переполнение разрядной сетки не возникает.

Пример.Сложить числа Х=+0.101и У= -0.001в дополнитель­ных кодах:

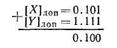
В данном примере возник перенос единицы (Р_о=1) из знакового разряда, который игнорируется. Кроме того, возник перенос единицы (Р₁=1) из стар­шего числового разряда в знаковый. Следовательно, Р₀ 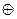Р₁=0, что свиде­тельствует об отсутствии переполнения разрядной сетки.

Пример.Сложить положительные числа Х=0.101; У=0.100:

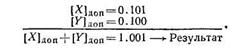
Преобразователи кодов (ПК).Предназначены для преобразования одного параллельного кода в другой. Они используются для шифрации и де­шифрации цифровой информации и могут иметь п входов и k выходов. Соот­ношения между числами n и k могут быть любыми: n = k, n < k и n > k.

По назначению ПК можно разделить на два типа: с невесовым и с весо­вым преобразованием кодов. В преобразователях первого типа отсутствует численная взаимосвязь входного и выходного кодов, а имеет место символь­ная взаимосвязь, например преобразование двоично-десятичного кода в код семисегментного индикатора десятичных цифр. Преобразователи второго типа используются, как правило, для преобразования числовой информации, тогда между числами входного и выходного кодов имеет место заданная математическая взаимосвязь.

Преобразование n-элементного кода в k-элементный можно осуществить с предварительной дешифрацией первого кода и без нее. В первом случае сначала дешифрируется n-элементный код и на каждой из 2ⁿ выходных шин получается сигнал, соответствующий одной из входных кодовых комбинаций. Затем каждый из выходных сигналов кодируется в k-элементном коде при по­мощи шифратора.

Рассмотрим в качестве примера преобразование трехэлементного кода в пятиэлементный согласно табл. 1. Схема, реализующая такой ПК, пока­зана на рис. 5. В качестве дешифратора используется полный дешифра­тор 3×8, а в качестве шифратора – диодный матричный шифратор.

Во втором случае при построении ПК без предварительной дешифрации

входного кода достаточно в соответствии с заданными условиями преобразования составить структурные формулы для каждого из элементов того ко­да, в котором следует преобразовать заданный код, и затем составить схему ПК.

ПК с невесовым преобразованием кодов, как правило, описываются таблицами истинности, однозначно определяющими входной и выходной коды.

ПК с весовым преобразованием достаточно часто используются для чис­ленного преобразования одной непрерывной функции в другую (например, sinα в cosα) путем их дискретизации, определения входных и выходных ко­дов каждой функции в одни и те же моменты дискретизации, и уже на осно­вании этих колов строится схема ПК. В этих случаях разрядность кода определяет точность преобразования, так как с ее увеличением увеличивается точность аппроксимации непрерывной функции ее дискретным эквивалентом.

Таблица 1.

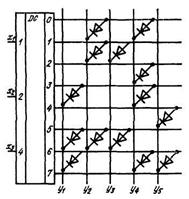
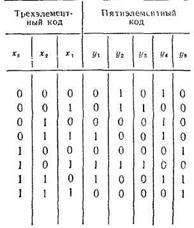
Рис. 5. Схема реализующая ПК.