Простейшие ЛЭ имеют следующие характеристики. 3 страница

Рис. 5. Схема регистра, выполняющего операцию

поразрядного сложения по модулю 2.

Табл. 1 является таблицей состояний для операции Q_i=x_i 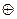y_i.Пусть в регистре Рг на триггерах со счетными входами за­писан код числа х₁, х₂, . . .x_n-1, x_n. По сигналу приема кода Пр через систему схем И на счетные входы триггеров в каждом разряде можно передать сигналы 1 кода числа у_1,у_2…..у_п-1,,у_п. Пройдя на счетный вход, сигналы 1 вызовут переброс всех триггеров, которые предварительно сигналами кода х₁, х₂, . . .x_n-1, x_n были установлены в состояния 1 и 0, и в регистре Рг образуется код числа Q_1,Q₂...Q_n-1,Q_n как результат поразрядного сложения по модулю 2.

Рассмотрим выполнение логических операций сложения и умно­жения. Состояния микроопераций приведены соответственно в табл. 2 и 3. На рис. 6 приведена схема для выполнения опера­ций поразрядного логического сложения и умножения.

Таблица 1 Таблица 2 Таблица 3

В регистре Рг2 записан код числа х₁, х₂, . . .x_n-1, x_n. Код второго чис­ла у_1,у_2….. у_п-1,,у_п хранится в регистре Pг1, и он может быть передан в регистр Рг2 через систему логических элементов И₁или И₂. При воз­буждении шины передачи сигналом ЛС логического сложения через схемы И₁ на входы S триггеров регистра Рг2 пройдут сигналы, соот­ветствующие состояниям 1 триггеров регистра Pг1. Следовательно, состояние 1 триггеров регистра Pг1 переносится при передаче в триггеры регистра Рг2 и объединяется в каждом триггере регистра Рг2 с их состояниями 1, установленными кодом х₁, х₂, . . .x_n-1, x_n.

Рис. 6. Схемы регистров, выпол­няющих операции

логического ум­ножения и логического сложения.

Это и соответствует выполнению операции поразрядного сложения ко­дов в соответствии с табл. 2. При возбуждении шины передачи сиг­налом ЛУ логического умножения через систему логических схем И₂ в регистр Рг2 на входы 0 триггеров будут переданы сигналы, соответствующие состоянию инверсных выходов триггеров регистра Рг1. В этом случае произойдет сброс всех триггеров регистра Рг2, кроме тех, состояние 1 которых соответствовало состоянию 1 триггеров регистра Рг1. Следовательно, выполнение указанной передачи сигналов приводит к выполнению операции поразрядного логического умножения в соответствии с табл. 3.

Литература:

1. В.В. Стрыгин «Основы вычислительной, микропроцессорной техники и программирования» стр: 95-97.

2. Э.В. Евреинов «Цифровая и вычислительная техника» стр: 115-116.

3. Б.Я. Лихтциндер «Микропроцессоры и вычислительные устройства в радиотехнике» стр: 65.

ЗАНЯТИЕ 1.1.5 Основные функции, выполняемые шифратором. Схемы шифраторов. Клавиатурные шифраторы. Основные функции дешифраторов. Линейный, прямоугольный, пирамидальный дешифраторы. Синтез схемы дешифраторов. Принцип построения схем дешифраторов.

ВОПРОСЫ ЗАНЯТИЯ:

1. Назначение дешифраторов. Линейный, прямоугольный, пирамидальный дешифраторы, принципы построения схем дешифраторов.

2. Основные функции, выполняемые шифратором. Схемы шифраторов. Клавиатурные шифраторы.

ПЕРВЫЙ ВОПРОС.

Дешифратор (декодер) — это комбинационное устрой­ство с несколькими входами и выходами, у которого определенным комбина­циям входных

сигналов соответствует активное состояние одною из выходов. Дешифраторы преобразуют двоичный и двоично-десятичный коды в унитар­ный код, т. е. код двоичного n-разрядного числа, представленного 2^п разря­дами, только один из разрядов которого равен 1.

Дешифраторы могут быть полными и неполными. У полного дешифра­тора п входам соответствует 2ⁿ выходов. У неполного дешифратора число вы­ходов т < 2ⁿ.

Дешифратор представля­ет собой совокупность схем И, формирующих управляющий сиг­нал на одном из выходов, в то время как на остальных выходах сиг­налы отсутствуют. В табл. 1 отражены возможные состояния де­шифратора на три входа (п=3) и восемь выходов.

Таблица 1.

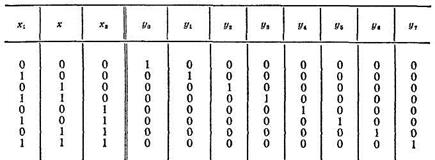
Выходы дешифратора имеют нумерацию, совпадающую с деся­тичным представлением двоичного числа от 0 до п—1. Если, на­пример, слово на входе имеет код 101 (табл. 1), то единичный сигнал будет только на пятом выходе дешифратора, т. е. у₅= 1. Действительно, если на элемент И₅ поступает код 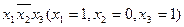, то на всех выходах дешифратора, кроме у₅, будут ло­гические 0.

Число элементов одноступенчатого дешифратора определяется числом выходов.

По способу организации дешифрации слова дешифраторы подразделяют на одноступенчатые (линейные) и многоступенчатые (прямоуголь­ные, пирамидальные).

По типу используемых элементов различают дешифрато­ры диодные, транзисторные и магнит­ные. На этих элементах составляются схемы И, которые и используются в дешифраторах. В настоящее время схе­мы дешифраторов выпускаются в интег­ральном исполнении.

Для схемной реализации каждого выхода дешифратора доста­точно иметь один логический элемент И с числом входов, равным числу входов дешифратора.

Прямые и инверсные значения переменных обычно поступают на входы дешифратора с прямых и инверсных выходов триггеров регистра, на котором записывается входная комбинация перемен­ных. Каждый выход дешифратора принима­ет значение, равное еди­нице (возбуждение), только при одном оп­ределенном наборе вход­ных переменных х₁—х₃. Если длина дешифри­руемого двоичного сло­ва больше возможного числа входов элементов И, входящих в комплекс, используют многоступенчатое (каскадное) построение де­шифратора.

Известны три основные структуры дешифраторов: матричная (линей­ная), каскадная и пирамидальная.

Матричные (линейные) дешифраторы состоят из 2ⁿ логических схем совпадения, каждая из которых имеет п входов. На входы этих логических элементов подаются все возможные комбинации прямых и инверсных разря­дов дешифрируемого числа X. Пример матричного дешифратора 3×8 при­веден на рис. 1, а, а его условное обозначение—на рис. 1, б.

Рис. 1. Схема матричного дешифратора 3×8 (а),

и его условное графическое обозначение (б).

Матричные дешифраторы имеют самое высокое быстродействие. Время задержки появления сигнала на выходе в дешифраторах с n-входными логи­ческими элементами составляет время задержки одного элемента (t_з∑ = t₃), но их недостаток — большое число входов логических элементов с ростом разрядности. Этот недостаток менее существен при использовании диодной логики. Пример схемы дешифратора 3×8, выполненного на диодной логи­ке, приведен на рис. 2. Для того чтобы такой дешифратор обладал свойст­вом наращиваемости для увеличения разрядности входного числа, он дол­жен строиться из одинаковых схем (на рис. 2 обведены пунктирной лини­ей). Так, матричный дешифратор 2×4 может быть построен на основе двух таких схем, дешифратор 3×8 — на основе трех схем, дешифратор 4×16 — на основе 8 схем, дешифратор 5×32 — на основе

20 схем и т. д.

При каскадном построении дешифраторов входное число разбивается на несколько подчисел, количество которых может находиться в диапазоне от 2

до . При нечетном значении п количество подчисел округляется в сторо­ну ближайшего большего целого числа. Для каждого подчисла формиру­ются все его минтермы путем построения отдельных матричных дешифраторов. Все дешифраторы подчисел составляют первый каскад дешифратора. В каждом последующем каскаде образуют конъюнкции минтермов из преды­дущего каскада. В зависимости от n и числа входов логических элементов каскадный дешифратор можно выполнять в различных вариантах, отли­чающихся числом каскадов, числом матричных дешифраторов и т. п. При­меры каскадного дешифратора на двух- и трехвходовых элементах при п = 8 приведены на рис. 3, а и б.

Рис. 2. Пример схемы дешифратора 3×8,

выполненного на диодной логи­ке.

Рис. 3. При­меры каскадного дешифратора на двух-

и трехвходовых элементах при п = 8.

Быстродействие каскадных дешифраторов определяется числом каскадов т, а суммарное время задержки t_3∑= mt₃.

Пирамидальный дешифратор отличается от каскадного тем, что в его каскадах каждая конституента единицы формируется как конъ­юнкция одной из конституент предыдущего кас­када и одного из разрядов входного числа, еще не использовавшегося для формирования кон­ституент. Принцип построения пирамидального дешифратора иллюстрируется рис. 4. Коли­чество каскадов пирамидального дешифратора равно п — 1, а суммарное время задержки сигнала t_з∑ = t₃(n — 1).

Рис. 4. Принцип построения пирамидального дешифратора.

В интегральной схемотехнике особый интерес представляют методы син­теза дешифраторов на однотипных модулях. Для реализации дешифратора на n входов из набора однотипных модулей строится многокаскадная схема. Принцип ее построения поясняется рис. 5. К управляющим входам каждого из модулей М₁, М₂, . .. , M_2n-s подключено по одному выходу от каждого дешифратора DC₁, DC₂, .... DC_r, где s — число информационных входов модуля, r — число управляющих входов модуля.

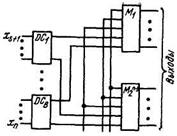
Рис. 5. Принцип построения дешифратора на

n входов из набора однотипных модулей.

Дешифраторы можно использовать для реализации логических функции согласно заданной таблице истинности. Пусть, например, функция F (х₁, х₂, х₃) задана единичными значениями на номерах наборов 1, 2, 4, 5, 7 и нулевыми на наборах 0, 3 и 6. Совершенная дизъюнктивная форма этой функции имеет вид

F = m₁ + m₂ + m₄ + m₅ + m₇, (1)

где mi — конституента единицы i-го набора.

Совершенная конъюнктивная форма функции

(2)

Для построения схемы Достаточно иметь дешифратор 3×7 и соединить его прямые выходы согласно уравнению (1) (рис. 6, а) или инверсные выходы согласно уравнению (2) (рис. 6, б).

Рис. 6. Пример использования дешифратора для реализации логических функций.

Дешифраторы входят в виде функциональных узлов в состав несколь­ких серий ТТЛ и КМОП. В качестве примера на рис. 7, а приведено услов­ное обозначение микросхемы дешифратора 4×16 типа К155ИДЗ. Микро­схема имеет четыре адресных входа D0...D3, два разрешающих входа и 16 выходов, пронумерованных от 0 до 15. Если на обоих разрешающих входах поддерживается уровень V0 = V1 = 0, микросхема работает как дешифра­тор. Потенциал U¹ на любом из разрешающих входов установит уровень U¹ на всех выходах независимо от состояния входов. Для наращивания раз­рядности (например, получения дешифратора 5×32) шины младших че­тырех разрядов соединяют с входами D0...D4 обеих микросхем, а сигналы старшего разряда подают в прямом виде на один из разрешающих входов первой микросхемы, в инверсном — на разрешающий вход второй. Вторые разрешающие входы заземляются.

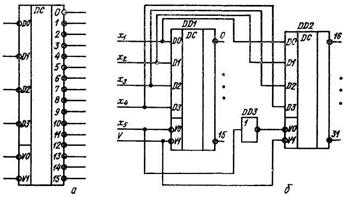
Рис. 8. Услов­ное обозначение микросхемы дешифратора 4×16

типа К155ИДЗ (а), схема получения дешифратора 5×32 (б).

На рис. 1 показаны условное гра­фическое обозначение и схема дешифратора К155ИДЗ.

При V₁ = V₂ = 0 дешифратор реализует инверсии всех конъюнкций входных переменных, а при всех остальных наборах V₁и V₂на выходах дешифратора будут уровни «1».

Входы V₁и V₂ служат для стробирования дешифра­тора и для расширения числа его информационных вхо­дов и выходов.

На рис. 2 приведена схема дешифратора на 32 вы­хода, построенная на ИС К155ИДЗ.

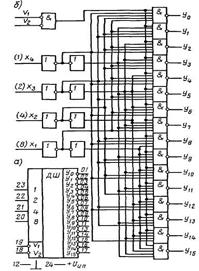
Рис. 1. Условное графическое обозначение (а)

исхема (б) дешифратора К155ИДЗ.

Так как дешифратор реализует все конъюнкции (или их инверсии), он может быть использован для реализации одной или нескольких функций алгебры логики от переменных, подаваемых на информационные входы дешифратора.

Рис. 2. Схема дешифратора 1 из 32.

На рис. 3 показан пример реализации четырехфазной системы синхронизации с неперекрывающимися им­пульсами. Входные переменные поступают с 4-разрядного двоичного счетчика.

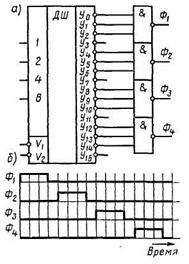
Рис. 3. Схема четырехфазного генератора синхросигналов (а)

и временная диаграмма его работы (б).

ВТОРОЙ ВОПРОС.

Шифратором называется комбинационное устройство, преобразующее унитарный код, подаваемый на входные шины, в соответству­ющий код на выходных шинах. Таким образом, шифраторы выполняют функ­цию, обратную функции, выполняемой дешифратором. Если с выходных шин шифратора снимается n-разрядный код, то максимальное число вход­ных шин определяется числом возможных кодовых комбинаций и состав­ляет 2ⁿ.

Рассмотрим в качестве примера синтез шифратора с пятью входами, преобразующего унитарный код в двоичный. Фрагмент таблицы истинности этого шифратора приведен в виде табл. 1. На остальных наборах входных переменных выходные функции имеют безразличные значения. Уравнения, описывающие функции F₁, F₂ и F₃, наиболее удобно представить в следу­ющем виде:

F₁ = x₅ + x₃ + x₁;F₂ = x₄ + x₃;F₃ = x₂ + x₁.(3)

Наиболее просто шифраторы реализуются на диодной логике. Так, для приведенного примера диодный шифратор должен иметь пять входных и три выходных шины, причем каждая входная шина соединяется через диоды с выходными в соответствии с уравнениями (3) (см.рис. 9) или непосред­ственно по таблице истинности (табл. 1).

Если шифраторы, разрабатываемые на отдельных логических элементах, преобразуют унитарный входной код практически в любой выходной парал­лельный код соответствующей разрядности, то шифраторы, выполненные в виде микросхем, как правило, преобразуют сигнал, поданный только на один вход (например, 9), в выходной параллельный двоичный код (в данном случае 1001).

Таблица 1.

Рис. 9. Схема шифратора на диодной логике.

В микросхемах шифраторов для того, чтобы он откликался на сигнал только одного входа, его схему делают приоритетной. Тогда выходной код должен соответствовать номеру «старшего» входа, получившего сигнал. Пред­положим, что активные уровни поступили на входы с номерами 3, 4 и 9. Стар­ший по номеру вход здесь 9, он обладает приоритетом, поэтому выходной код шифратора 1001.

Типичным примером яв­ляется шифратор клавиатуры для ввода в цифровое ус­тройство шестнадцатеричного кода (рис. 4).

При ненажатых клавишах на всех входах шифратора обеспе­чивается «0», а нажатая клавиша подает на соответству­ющий вход шифратора «1». Шифратор вырабатывает также осведомительный сигнал Z при нажатии любой из клавиш.

Рис. 4. Схема шифратора клавиатуры.

Уравнения, описывающие структуру шифратора, имеют следующий вид:

Литература:

1. В.А. Скаржепа, В.И. Сенько «Электроника и микросхемотехника» сборник задач, стр: 118-122.

2. Л.Н. Преснухин «Микропроцессоры» ч. II, стр: 118-121.

3. В.В. Стрыгин «Основы вычислительной, микропроцессорной техники и программирования» стр: 102-105.

ЗАНЯТИЕ 1.1.6 Назначение, классификация, параметры счетчиков.

ВОПРОСЫ ЗАНЯТИЯ:

1. Назначение и классификация счетчиков.

2. Параметры счетчиков.

3. Основные понятия двоичного счета и счетчика.

ПЕРВЫЙ ВОПРОС.

Счетчик– последовательное цифровое устройство, предназначенное для подсчета числа импульсов (сигналов) поступающих на его вход, и фиксации этого числа в виде кода, хранящегося в триггерах.

Микрооперация счета заключается в изменении значения числа С в счетчике на ± 1. Счетчик в котором выполняется микрооперация счета С: = С + 1, называется суммирующим, а счетчик, реализующий микрооперацию С: = С – 1, - вычитающим. Если реализуются обе микрооперации, счетчик называют реверсивным.

Количество разрядов счетчика определяется наибольшим числом, которое должно быть получено в конкретном случае.

Счетчики обычно реализуются на Т-триггерах. На практике для построения Т-триггера применятся D-триггеры и JK-триггеры.

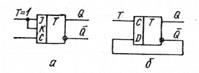
Рис. 1. Тактируемые Т-триггеры на основе:

JK-триггера (а) и D-триггера (б).

Для счета и выдачи результата в счетчиках имеется один вход и n-выходов, в зависимости от количества разрядов.

При маркировке для обозначения счетчика используются буквы ИЕ. Конструктивно счетчики выполняются в виде совокупности интегральных схем – триггеров, соединенных соответствующим образом, или в виде одной интегральной схемы, содержащей многоразрядный счетчик.

Счетчики широко применяются в вычислительной технике и различных устройствах дискретной автоматики: для формирования адресов, команд, счета количества циклов операций, формирования кода в аналого-цифровых преобразователях, отсчета временных отрезков в таймерах и т.д.

Классификация счетчиков:

1. По целевому назначению: простые (суммирующие и вычитающие) и реверсивные.

На простые счетчики сигналы поступают с одним знаком, т.е. они переходят от состояния к состоянию только в одном направлении: либо +1, либо -1.

В суммирующем счетчике каждый сигнал увеличивает его состояние на 1, в вычитающем уменьшает его показание на 1.

В реверсивном счетчике может выполняться как операция увеличения показаний, так и уменьшения.

2. По способу организации счета: асинхронные и синхронные.

В асинхронных счетчиках сигнал от разряда к разряду передается в различные интервалы времени, в зависимости от состояния входных сигналов.

В синхронных счетчиках сигналы от разряда к разряду передаются с помощью тактовых сигналов.

3. По способу организации цепей переноса между разрядами различают счетчики: с последовательным, параллельным и групповым переносом.

При последовательном переносе, перенос в соседний старший разряд формируется только после переключения триггера в предыдущем разряде (младшем).

При параллельном переносе, переносы формируются одновременно для всех разрядов.

В счетчиках с групповым переносом разряды счетчика разбиваются на группы. В пределах одной группы обычно организуется параллельный перенос, а между группами последовательный.

4. По виду кодирования внутренних состояний счетчика: с двоичным кодирование, одинарным кодированием, унитарным кодированием.

В счетчиках с двоичным кодированием К_сч = 2ⁿ , для получения 2-10 счетчика, шесть его состояний из 16 отключаются. В зависимости от выбора системы счисления можно получить счетчики с кодами: 8-4-2-1, 4-2-2-1 и т.д. один из вариантов код Грея: при возрастании десятичного числа на 1, изменяется значение только одного символа по сравнению с другим двоичным числом. Код Грея используют при преобразовании угла поворота кодирующего диска в цифровой код для уменьшения ошибки при считывании.

В счетчиках с одинарным кодированием, состояния отличаются при перемещении по кольцу единственного сигнала 0 или 1.

Состояние унитарных счетчиков определяется числом отдельных состояний каскадов.

ВТОРОЙ ВОПРОС

Основными характеристиками счетчика являются модуль счета (К_сч), который иногда в технической литературе называют периодом счета или коэффициентом пересчета; разрешающая способность; время регистрации (быстродействие) и емкость.

Основной характеристикой счетчика является модуль счета К_сч, определяемый максимальным числом единичных сигналов, которое может быть сосчитано счетчиком. Счетчик, содержащий n двоичных разрядов, может находиться в состояниях 0, 1, 2, …, 2ⁿ - 1. При поступлении на вход суммирующего счетчика 2ⁿ –й единицы он переходит из состояния 2ⁿ - 1 в состояние 0. Таким образом, n-разрядный суммирующий двоичный счетчик имеет модуль счета К_сч = 2ⁿ.

Быстродействие счетчика характеризуется частотой поступления счетных импульсов f_сч и временем установки счетчика t_уст. Параметр f_сч характеризует максимальную частоту поступления счетных импульсов на вход счетчика.

Для счетчиков, срабатывающихпо уровню тактового импульса, время установки кода счетчика характеризует максимальный временной интервал между моментом поступления счетного импульса и моментом установления кода счетчика. Для счетчиков, работающих в режиме с внутренней задержкой, t_уст определяется максимальным временным интервалом между моментом окончания счетного импульса и моментом установления кода счетчика. Предполагается, чтосчитывание кода осуществляется параллельно со всех разрядов счетчика.

Разрешающая способность – минимально допустимый период следования входных сигналов, при котором обеспечивается надежная работа счетчика. Чем больше частота поступления счетных сигналов, тем большее быстродействие требуется от счетчика.

Емкость счетчика – максимальное число единичных сигналов, которое может быть зафиксировано на счетчике. Эта характеристика счетчика зависит от основания системы счисления и числа разрядов.

ТРЕТИЙ ВОПРОС

Теперь поясним понятия двоичного счета и счетчика. Двоич­ный счет осуществляется двоичными триггерными счетчиками. Они представляют собой цепочку триггеров (обычно Т-триггеров), соединенных определенным образом. Выход Q предшест­вующего триггера соединен с входом Т последующего (рис. 2). В качестве Т-триггера можно использовать надлежащим обра­зом включенные D- или JK-триггеры. На рис. 4 приведена схема трехразрядного триггерного двоичного счетчика, собран­ного из D-триггеров, которые включены как Т-триггеры.

В двоичной системе счисления каждое число представляется только двумя символами: 1 и 0, совокупность которых назы­вается битом. Термин «символы», а не «цифры», применен по­тому, что 1 здесь означает наличие, а 0 – отсутствие двоичной единицы. Вес каждого разряда бита зависит от занимаемого им места. Например, вес самого младшего разряда равен 2⁰=1. Вес второго разряда, слева от младшего, равен 2¹ = 2, третьего - 2² = 4 и т. д.

Рис. 2. Двоичный счетчик с Т-триггерами

Вход R — установка нулевого со­стояния.

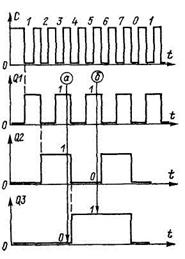
Рис. 3. Временная диаграмма работы

двоичного счетчика с Т-триггерами.

В табл. 1 представлены десятичные числа от 0 до 15 и их эквиваленты в двоичном коде. Нетрудно видеть, что каждое десятичное число можно представить как сумму чисел 1, 2, 4, 8 и так далее, представляющих собой сте­пени числа 2.

Таблица.1. Представление десятичных

чисел в двоичном коде.

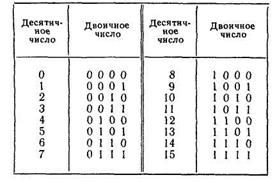
Рис. 4. Двоичный счетчик сD-триггерами

В качестве примера приведем структуру десятичного числа 13 в двоичном коде:

Цепочкой из Т-триггеров (рис. 2) осуществляется счет и регистрация импульсов в двоичном коде. Это видно на временной диаграмме. Выход первого триггера устанавливается в единичное состояние после каждого второго входного импульса, выход второго триггера – после каждого четвертого импульса, выход третьего триггера - после каждого восьмого импульса и т. д. Триггеры DD1, DD2, DD3 делят вход­ные импульсы соответственно на 2, на 4, на 8, после чего состо­яния триггеров повторяются. На рисунке показано, что актив­ный (переключающий) перепад входных импульсов - отрица­тельный: от высокого уровня к низкому. Из последних трех эпюр временной диаграммы видно, что состояния триггеров от­вечают в двоичном коде порядковому номеру воздействующего импульса. Так, например, после третьего входного импульса (стрелка а на рисунке) состояние, или содержимое, счетчика таково: Q1 =1l; Q2=1; Q3=0, т. е. число, записанное счетчи­ком, равно 011. Здесь первый триггер соответствует младшему разряду числа, а последний — старшему. После пятого вход­ного импульса (стрелка б на рисунке) содержимое счетчика бу­дет 101.

На основе рассмотренных схем (рис. 2 и 4) можно со­ставить двоичный счетчик с произвольным пределом счета. Не­обходимо только набрать цепочку триггеров. Число триггеров легко определить, если воспользоваться табл. 2. Состояния двоичного счетчика даны в табл. 3.

Таблица 2. Зависимость между числом триггеров и

числом возможных состояний двоичного счетчика.

До сих пор мы полагали, что связь между триггерами осуществляется со­единением выхода Q предшествующе­го триггера с входом Т последующего. В этом случае состояния триггеров чередуются в направлении сверху вниз (табл. 3) и, как следует из таб­лицы, каждый новый импульс на вхо­де увеличивает содержимое счетчика на 1. Такие счетчики как мы уже знаем называют сум­мирующими. Если вход Т триггера со­единен с выходом Q предшествующего, то поступление каждого оче­редного входного импульса уменьшает на 1 содержимое счетчика: состояния триггеров череду­ются в направлении снизу вверх (табл. 3). Такой счетчик на­зывают вычитающим. Рекомендую студентам самим начертить схему вычитающего счетчика и его временную диаграмму.

Таблица 3. Состояния двоичного триггерного счетчика

Для обоих видов счетчиков (суммирующих и вычитающих), составленных из триггеров, предел счета, т. е. число возмож­ных состояний, равен 2ⁿ. Далее, если на вход поступают новые импульсы, цикл счета повторяется. Это следует и из временной диаграммы.