Центральное проецирование
ПРЕДМЕТ И МЕТОД НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ
Начертательная геометрия, являясь одной из ветвей геометрии, относящейся к математике, имеет ту же цель, что и геометрия вообще: изучение форм предметов окружающего нас материального мира и отношений между ними, установление закономерностей и применение их к решению практических задач.
В начертательной геометрии для решения задач используется графический путь, все геометрические свойства фигур изучаются по чертежу, т.е. чертеж является основным средством изучения свойств пространственных фигур.
Для того чтобы чертеж был геометрически равноценен изображаемой фигуре (оригиналу), он должен быть построен по определенным геометрическим законам - правилам. В начертательной геометрии чертежи строятся при помощи метода проецирования, поэтому получаемые таким образом чертежи называют проекционными.
Таким образом, содержанием курса начертательной геометрии является:
· исследование способов построения проекционных чертежей;
· решение геометрических задач, относящихся к пространственным фигурам;
· применение способов начертательной геометрии к исследованию и решению практических и теоретических вопросов науки и техники.
В наше время нет такого вида человеческой деятельности где не применялись бы чертежи - будь то технические, строительные, географические и топографические (карты) и др. Все они строятся по правилам проецирования.
Основные задачи курса
1. Изучить теоретические основы образования чертежа.
2. Изучить алгоритмы решения позиционных и метрических задач.
Позиционные задачи - задачи на взаимную принадлежность и пересечение геометрических фигур.
В начертательной геометрии все фигуры и предметы отображаются на плоскость двумя основными способами: центральным проецированиемилипараллельным проецированием.
Метрические задачи-задачи на определение натуральных величин расстояний, углов геометрических фигур.
СПОСОБЫ ПРОЕЦИРОВАНИЯ
Геометрической фигурой называют любое множество точек. Геометрических фигур существует много, но основных только три - точка, прямая (линия) и плоскость.
Центральное проецирование
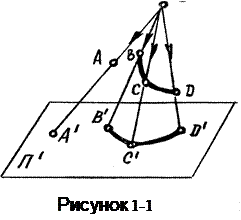
 Пусть в пространстве дана некоторая плоскость П¢, которую называют плоскостью проекций, и вне этой плоскости точка S , называемая центром проецирования. Чтобы спроецировать точку А пространства на плоскость П' нужно через центр проецирования S и точку А провести прямую (проецирующий луч) до пересечения ее с плоскостью П' в точке A’ ТочкуА’называют центральной проекцией точки А (рисунок 1-1).
Пусть в пространстве дана некоторая плоскость П¢, которую называют плоскостью проекций, и вне этой плоскости точка S , называемая центром проецирования. Чтобы спроецировать точку А пространства на плоскость П' нужно через центр проецирования S и точку А провести прямую (проецирующий луч) до пересечения ее с плоскостью П' в точке A’ ТочкуА’называют центральной проекцией точки А (рисунок 1-1).
Если возьмем произвольную криволинейную фигуру, то все проецирующие лучи образуют проецирующую коническую поверхность, поэтому этот способ проецирования называют еще коническим способом.
Дата добавления: 2015-11-06; просмотров: 559;
