Параллельное проецирование
Широкое распространение в практике получил частный случай центрального проецирования, когда центр проецирования S удален в бесконечность от плоскости проекций П¢. Проецирующие лучи при этом практически параллельны между собой, поэтому данный способ получил название параллельного проецирования, а полученные с его помощью изображения (проекции) фигуры на плоскости называют параллельными проекциями.
|
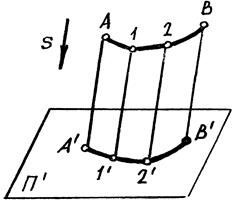
Возьмем в пространстве какую-либо фигуру, например линию АВ (рисунок1-2). Спроецируем ее на плоскость проекций П¢. Направление проецирования укажем стрелкой S. Чтобы спроецировать точку А на плоскость П¢ надо провести через эту точку параллельно направлению S прямую линию до пересечения с плоскостью проекций П¢. Полученная точка А¢ называется параллельной проекцией точки А. Аналогично находим проекции других точек линии АВ.
Совокупность всех проецирующих лучей определяет (представляет) в пространстве цилиндрическую поверхность, поэтому такой способ проецирования называют цилиндрическим.
2.3Основные свойства параллельного проецирования
1) Проекцией точки является точка. АÞА¢ (рисунок 1-3а).
 |
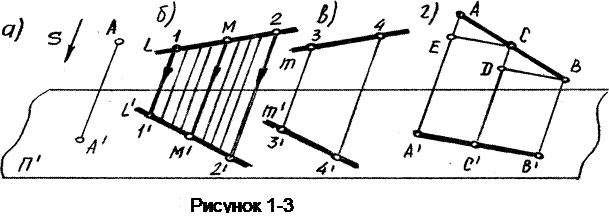2) Проекцией прямой является прямая (свойство прямолинейности).
Действительно, при параллельном проецировании все проецирующие лучи будут лежать в одной плоскости Е. Эта плоскость пересекает плоскость проекций по прямой линииl¢ (рисунок 1-3б).
3) Если в пространстве точка принадлежит линии (лежит на ней), то проекция этой точки принадлежит проекции линии (свойство принадлежности), (рисунок 1-Зб, точка М).
4) Проекции взаимно параллельных прямых также взаимно параллельны, т.к.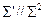 
(рисунок 1-3б, в), (l)ll(m)Þ (l¢) II (m').
5) Если отрезок прямой делится точкой в некотором отношении, то проекция отрезка делится проекцией этой точки в том же отношении.
Докажем это: введем СЕ//A’С' и DВ//С'B', тогда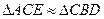 
. Из подобия треугольников следует, что
½АС½/½СВ½=½СЕ½/½DB½=½A¢C¢½/½C¢B¢½.
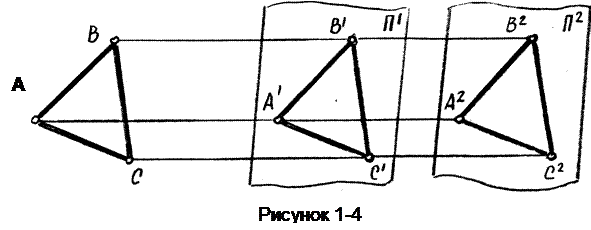
6) Параллельный перенос плоскости проекций или фигуры (без поворота) не меняет вида и размеров проекции фигуры (рисунок1-4).
2.4 Прямоугольное проецирование
Частный случай параллельного проецирования, при котором направление проецирования S перпендикулярно плоскости проекций П¢, еще больше упрощает построение чертежа и наиболее часто применяется в конструкторской практике. Этот способ называют прямоугольным проецированием или (что тоже) ортогональным проецированием.
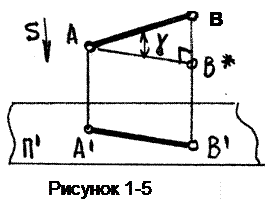
Метод ортогональных проекций был впервые изложен французским геометром Гаспаром Монжем, поэтому иногда его называют методом Монжа. Этот метод является основным при составлении технических чертежей, поскольку позволяет наиболее полно судить о размерах изображенных предметов. В этом случае нетрудно установить соотношение между длиной некоторого отрезка АВ в пространстве и длиной его проекции А¢В¢(рисунок 1-5).
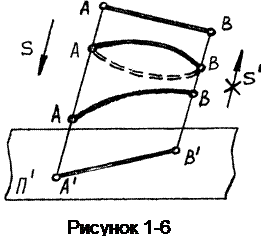
Рассмотренные способы проецирования позволяют однозначно решать прямую задачу - по данному оригиналу строить его проекционный чертеж. Однако только одна параллельная проекция без каких-либо дополнений недостаточна для полного представления о том, каким является этот предмет в натуре. По такому изображению (рисунок 1-6) нельзя определить не только форму и размеры предмета, но и его положение в пространстве, т.е. параллельная проекция не обладает свойством обратимости. Для получения обратимых чертежей проекционный чертеж дополняют необходимыми данными. Способы дополнения бывают различными. Мы в курсе начертательной геометрии будем рассматривать два вида обратимых чертежей:
1. комплексные чертежи в ортогональных проекциях;
2. аксонометрические чертежи.
Дата добавления: 2015-11-06; просмотров: 1001;