Лекция 5. Кинематический анализ зубчатых передач.
Вопросы, рассматриваемые на лекции. Классификация зубчатых передач. Геометрические элементы зубчатого колеса. Зубчатые механизмы с неподвижными осями. Планетарные механизмы. Дифференциальные механизмы.
Некоторые основные понятия.
Передаточное отношение отдельной зубчатой пары равно: 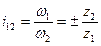 ,
,
где z1 и z2- числа зубьев ведущего и ведомого колес.
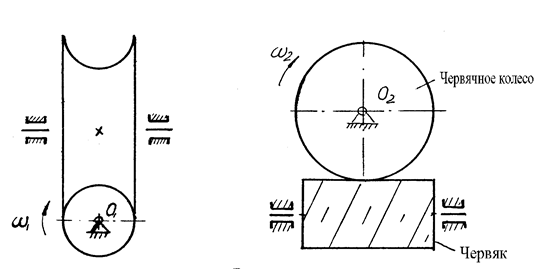 |
В случае червячной передачи (рис.8) через z1 обозначают число заходов червяка, а через z2- число зубьев червячного колеса.
Рис.8
Передаточное отношение зубчатой пары с внешним зацеплением (рис.9) имеет знак «минус», так как ведущее и ведомое колеса вращаются в противоположных направлениях, передаточное отношение пары с внутренним зацеплением (рис.10) - знак «плюс».
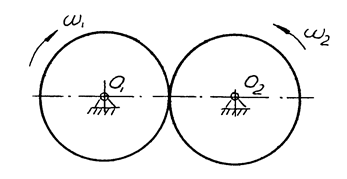
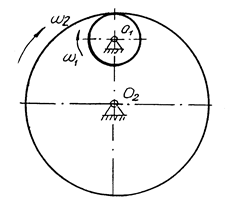 Рис.9 Рис.10
Рис.9 Рис.10
В случае реечного зацепления (рис.11) вращательное движение колеса с угловой скоростью w преобразуется в поступательное движение рейки со скоростью 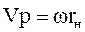 .
.
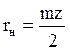 ,
,
где rн - радиус начальной окружности колеса;
m- модуль зацепления.
 |
При повороте колеса на угол, равный 360о, рейка продвигается на величину шага
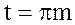 .
.
Рис.11 Рис.12
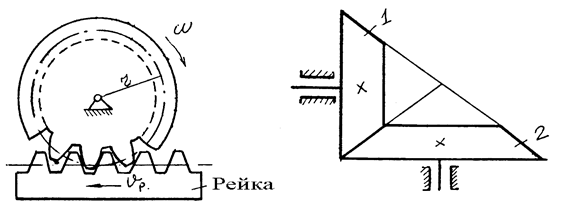
На рис.12 показана коническая зубчатая пара.
К зубчатым механизмам с подвижными осями относятся планетарные зубчатые механизмы (с одной степенью свободы) и дифференциальныезубчатые механизмы (с двумя степенями свободы). На рис.13 представлена одна из возможных схем дифференциального механизма.
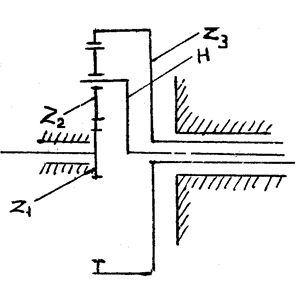 |
Рис.13
Соотношение между угловыми скоростями зубчатых колес и водилом дифференциального механизма определяется формулой:
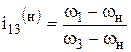 . .
| (4) |
Индекс «н» указывает, что в данном случае водило является неподвижным звеном, 1-ведущее звено, 3-ведомое звено.
Если колесо z3 закрепить неподвижно, то мы получим планетарный механизм. Передаточное отношение от зубчатого колеса z1 к водилу планетарного механизма определяется формулой:
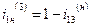 . .
| (5) |
Для подсчета кинетической энергии механизма, выбора подшипников при проектировании планетарных механизмов необходимо знать угловую скорость сателлитов. Поскольку скорость ведущего звена z1 задана и скорость водила может быть определена с использованием формулы (5), для определения угловой скорости сателлита необходимо знать передаточное отношение от центрального колеса z1 к сателлиту или от водила к сателлиту:
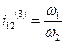 . .
| (6) |
Разделив числитель и знаменатель правой части выражения (6) на wн, получим:
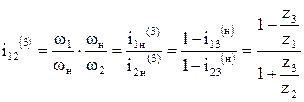 .
.
Тогда можно определить угловую скорость сателлита:
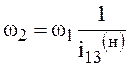 .
.
При определении передаточного отношения редуктора необходимо разделить его механизм на отдельные ступени. Прежде всего, следует выделить планетарную ступень, имея в виду, что в планетарную ступень входят водило, сателлиты и два центральных зубчатых колеса.
Планетарные и дифференциальные механизмы практически почти никогда не делаются с одним сателлитом, обычно сателлитов, входящих в зацепление с одними и теми же центральными колесами, несколько. Это делается для уменьшения сил инерции и разгрузки зубчатых колес механизма, уменьшения модуля зацепления и общих габаритов редуктора.
При определении числа степеней свободы следует иметь в виду, что все добавочные сателлиты (больше одного) являются пассивными связями.
Дата добавления: 2015-11-06; просмотров: 1582;
