Структурные уровни деформации, их классификация и масштаб
| № п/п | Структурные уровни | Масштаб |
| Макроуровень Вакансия, атом | 0,2 – 0,3 нм | |
| Перегиб, порог | 0,5 –5 нм | |
| Дислокация, уступ на границе зерна | 10 нм | |
| Группа дислокаций, сплетение, полоса скольжения, зона сдвига, дислокационная стенка, образования дисклинационного типа. Граница зерна. Доменные границы. Вакансионные, атомные кластеры и сегрегации. | 10 – 100 нм | |
| Мезоуровень Ячейка, дисклинационная петля, полоса в полосовой субструктуре, микродвойники, группы дисклинаций. Пластины и рейки мартенсита. Блок мозаики, фрагмент, субзерно. | 0,1 – 1 мкм | |
| Дислокационный ансамбль. Участок зерна или монокристалла. Пакет реек мартенсита. Зона сдвига, система скольжения | 1 – 20 мкм | |
| Уровень зерна Зерно. Дендрит. Зона сдвига, система скольжения. | 10 – 200 мкм | |
| Макроуровень Группа зерен. Волокно композита | 0,2 – 0,5 мм | |
| Участок образца | 1 мм | |
| Образец в целом | 1 – 10 мм |
Первым этапом работы является постановка задачи (1), включающая формулировку задания на основе анализа исходных данных о системе и прогнозирования научно-технического и социально-экономического эффекта. Постановка задачи завершается установлением класса разрабатываемой модели и соответствующих требований к ее точности, быстродействию, условиям эксплуатации и последующей корректировки, т.е. тех характеристик, которые составляют технические условия на новую разработку.
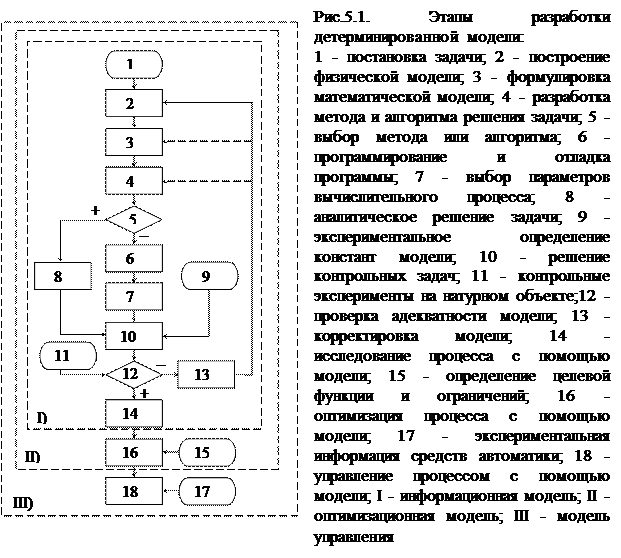
Следующим этапом (2) является формулировка физической модели на основе понимания сущности описываемого процесса, разделяемого в интересах его формализации на элементарные составляющие явления (тепло- и массообмен, гидродинамику, химические реакции, фазовые превращения и т.д.) и согласно принятой степени детализации - на агрегаты, зоны и ячейки (макро-, мезо- и микроуровень). При этом выясняется какими явлениями необходимо или целесообразно пренебречь, и в какой мере учесть взаимосвязь рассматриваемых явлений.
Каждому из выделенных явлений ставится в соответствие определенный физический закон (уравнение баланса) и устанавливаются начальные и граничные условия его протекания. Математическое описание этих соотношений - следующий этап (3), ведущий к формулировке математической модели.
В связи с неявным характером зависимости выходных параметров Y от входных переменных X в полученной модели необходимо выбрать удобный метод расчета (5) или разработать алгоритм решения задачи (4). В последнем случае необходимо составить и отладить программу (6), выбрать параметры вычислительного процесса (7). После чего осуществить контрольный счет (10). Для решения контрольных задач необходимы справочные или дополнительно экспериментально определенные константы, содержащиеся в математической модели (9).
Аналитическое решение (8) или алгоритм (6) и (7) в виде программы представляют новую форму модели, которая может быть использована для описания процесса, если будет установлена адекватность модели натурному объекту (12). Для проверки адекватности необходимо собрать экспериментальные данные (11) о значении тех факторов и параметров, которые входят в состав модели. Отрицательный результат проверки адекватности модели свидетельствует о ее недостаточной точности и может быть следствием различных причин. В частности может потребоваться переделка программы с целью реализации нового алгоритма или другого решения, не дающих столь большой погрешности. Возможна также корректировка математической модели или внесение изменений в физическую модель, если будет установлено, что пренебрежение рядом факторов является причиной неудачи. Любая корректировка модели (13) потребует повторного осуществления последующих этапов.
Положительный результат проверки адекватности модели позволяет изучать процесс путем проведения серии расчетов на модели (14), т.е. эксплуатации полученной информационной модели (I). Установление целевой функции и ограничений (15) с помощью теоретического анализа или экспериментов и включение в модель оптимизирующего математического аппарата (16) для обеспечения целенаправленной эволюции системы дает возможность построить оптимизационную модель (II). Адаптация полученной модели для управления производственным процессом в реальном масштабе времени (18) при включении в систему средств автоматического регулирования (17) завершает работу по созданию модели управления (III).
Последовательная корректировка информационной модели с целью повышения ее точности путем учета взаимного влияния факторов и параметров, введения дополнительных факторов и уточнения различных констант позволяет получить эвристическую модель, которая может быть инструментом для более глубокого изучения механизма явлений.
Лекция №6
Дата добавления: 2015-11-06; просмотров: 678;
