Моделирование детерминированных и стохастических процессов
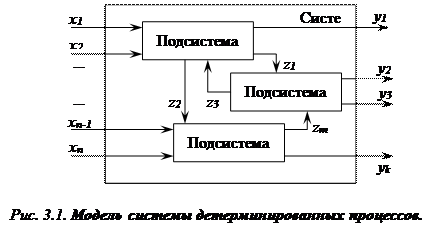
Математические модели связывают входные (независимые) переменные процесса X(x1,x2,...,xn ), называемые воздействиями, с выходными (зависимыми) характеристиками Y(y1,y2,...ym) (рис. 3.1), которые обычно именуют откликами, в виде уравнения связи
Y=f(X) (3.1)
 |
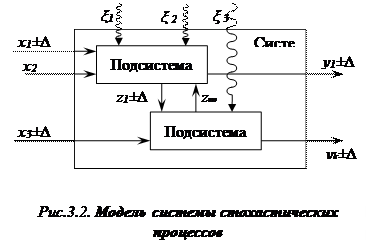 |
Любому реальному процессу свойственны случайные колебания, вызываемые физической изменчивостью каких-либо факторов xi±Dxi(t) или внешними случайными воздействиями. В силу этого при равном среднем значении входных характеристик X(t) в моменты t1 и t2 выходные параметры Y(t), будут неодинаковыми (рис.3.2). Поэтому для вероятностных процессов, где по сравнению с xi(t) нельзя пренебречь случайными колебаниями Dxi(t) и случайными внешними воздействиями xj(t), необходимо характеризовать систему с учетом статистического закона распределения мгновенных значений Y(t) относительно средней величины Yср(t)уравнением
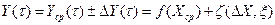 (3.2)
(3.2)
Модели, отображающие случайный (стохастический) характер параметров и факторов системы, называются статистическими или стохастическими в отличие от детерминированных, не учитывающих вероятностных характеристик процессов.
По мере уменьшения величины параметров DX и x уравнение (3.2) приближается по структуре к уравнению (1.1), описывающему детерминированные системы.
Обычно детерминированные модели (3.1), представляющие собой систему уравнений, удается составить только в тех случаях, когда о процессах в описываемой системе имеются ясные физические представления и эти представления можно формализировать. В таких случаях говорят, что система представляет собой «белый ящик» - объект с известной структурой и функциями.
Однако получаемая таким образом модель может оказаться громоздкой, а ее информационное обеспечение весьма трудоемким. Поэтому часто используют статистические модели для описания детерминированных систем. В таких случаях рассматривают систему как «черный ящик» с неизвестной структурой, в котором доступны для изучения только контролируемые входные параметры X и измеримые выходные характеристики Y. Получив таблицу соответствий {x1,y1; x2,y2;…; xn,yn}, принимают их за случайную выборку из генеральной статистической совокупности {X,Y} и описывают соотношением (3.2). Полученная статистическая модель при соответствующей интерпретации результатов позволяет раскрыть механизм, сделать «белыми» некоторые части устройства и функционирования «черного ящика».
Детерминированные модели (3.1), могут также использоваться для описания стохастических систем, если объектом изучения являются их усредненные характеристики. Таким образом, статистические модели являются более широким классом моделей и включают детерминированные модели как предельный частный случай, в котором выходные параметры Y однозначно определяются входными переменными X.
Соотношения (3.1) и (3.2) являются математическими моделями процессов, приближенно описывающими происходящие в системе изменения. Если доказано подобие натурных и моделирующих процессов, то можно говорить об адекватности моделей.
В зависимости от характера и пространственной структуры описываемых систем различаются модели с распределенными и сосредоточенными параметрами. В связи с различной интенсивностью моделируемых процессов во времени различают: статические модели, описывающие установившиеся процессы вблизи состояния равновесия; стационарные модели, характеризуемые постоянством основных параметров во времени; динамические модели систем, в которых входной переменной процесса является время.
В зависимости от конкретного вида применяемого математического аппарата, различают модели матричные, сетевые, дифференциальные, интегральные, алгоритмические, программные и др.
Лекция №4
Дата добавления: 2015-11-06; просмотров: 1769;
