Лекция 14. Радиоактивность. Закон радиоактивного распада.
Радиоактивность – самопроизвольное превращение неустойчивых изотопов одного элемента в изотопы другого элемента, сопровождающееся испусканием элементарных частиц или ядер.
1) Характеристики радиоактивности:
а) Время жизни радиоактивного ядра t - среднее время жизни большого числа одинаковых ядер (зависит от природы вещества; не зависит от внешних условий).
в) вероятность радиоактивного распада l - вероятность того, что ядро испытает превращение в единицу времени.
Связь между ними: 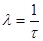 .
.
Радиоактивный распад - статистический процесс. Каждое радиоактивное ядро может распасться в любой момент и закономерность наблюдается только в среднем, в случае распада достаточно большого количества ядер.
Если в образце в момент времени t имеется Nрадиоактивных ядер, то количество ядер dN, распавшихся за время dt пропорционально N.
dN = -  Ndt. (9)
Ndt. (9)
Проинтегрировав (1) получим закон радиоактивного распада
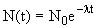 (10)
(10)
N0 - количество радиоактивных ядер в момент времени t = 0.
Период полураспада T1/2 - время, за которое первоначальное количество радиоактивных ядер уменьшится в два раза
T1/2 = ln2/  =0.693/
=0.693/  =
=  ln2 (11)
ln2 (11)
Активность A - среднее количество ядер распадающихся в единицу времени
A(t) =  N(t). (12)
N(t). (12)
Активность измеряется в кюри (Ки) и беккерелях (Бк)
1Ки = 3.7·1010 распадов/c,
1 Бк = 1 распад/c.
Распад исходного ядра 1 в ядро 2, с последующим его распадом в ядро 3, описывается системой дифференциальных уравнений
dN1/dt = -  1N1
1N1
dN2/dt = -  2N2 +
2N2 +  1N1, (13)
1N1, (13)
гдеN1(t) и N2(t) -количество ядер, а  1 и
1 и  2 - постоянные распада ядер 1 и 2 соответственно. Решением системы (13) с начальными условиями N1(0) = N10; N2(0) = 0 будет
2 - постоянные распада ядер 1 и 2 соответственно. Решением системы (13) с начальными условиями N1(0) = N10; N2(0) = 0 будет
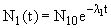 (14а)
(14а)
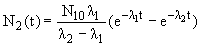 (14б)
(14б)
 Если
Если  2 <
2 <  1 (
1 ( 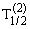 >
> 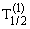 ), суммарная активность
), суммарная активность
N1(t)  1 + N2(t)
1 + N2(t)  2 будет монотонно уменьшаться.
2 будет монотонно уменьшаться.
Если  2 >
2 >  1 (
1 ( 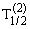 <
< 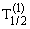 ), суммарная активность вначале растет за счет накопления ядер 2.
), суммарная активность вначале растет за счет накопления ядер 2.
Если  2 >>
2 >>  1, при достаточно больших временах вклад второй экспоненты в (14б) становится пренебрежимо мал, по сравнению со вкладом первой и активности второго A2 =
1, при достаточно больших временах вклад второй экспоненты в (14б) становится пренебрежимо мал, по сравнению со вкладом первой и активности второго A2 =  2N2 и первого изотопов A1 =
2N2 и первого изотопов A1 =  1N1 практически сравняются. В дальнейшем активности как первого так и второго изотопов будут изменяться во времени одинаково.
1N1 практически сравняются. В дальнейшем активности как первого так и второго изотопов будут изменяться во времени одинаково.
A1(t) = N10(t)  1
1 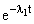 = N1(t)
= N1(t)  1 = A2(t) = N2(t)
1 = A2(t) = N2(t)  2. (15)
2. (15)
То есть устанавливается так называемое вековое равновесие, при котором число ядер изотопов в цепочке распадов связано с постоянными распада (периодами полураспада) простым соотношением.
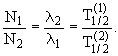 (16)
(16)
Поэтому в естественном состоянии все изотопы, генетически связанные в радиоактивных рядах, обычно находятся в определенных количественных соотношениях, зависящих от их периодов полураспада.
Лекция 15. Виды радиоактивного распада
Альфа-распад
Альфа-распад - распад атомных ядер, сопровождающийся испусканием альфа-частиц (ядер 4He).
Часть изотопов могут самопроизвольно испускать альфа-частицы (испытывать альфа-распад), т.е. являются альфа-радиоактивными. Альфа-радиоактивность за редким исключением (например 8Be) не встречается среди легких и средних ядер. Подавляющее большинство альфа-радиоактивных изотопов (более 200) расположены в периодической системе в в области тяжелых ядер (Z > 83). Известно также около 20 альфа-радиоактивных изотопов среди редкоземельных элементов, кроме того, альфа-радиоактивность характерна для ядер, находящихся вблизи границы протонной стабильности. Это обусловлено тем, что альфа-распад связан с кулоновским отталкиванием, которое возрастает по мере увеличения размеров ядер быстрее (как Z2 ), чем ядерные силы притяжения, которые растут линейно с ростом массового числа A.
Ядро альфа-радиоактивно, если выполнено условие, являющееся следствием закона сохранения энергии
M(A,Z) >M(A-4,Z-2) + Ma, (17)
где M(A,Z) и M(A-4,Z-2) - массы покоя исходного и конечного ядер соответственно, Ma- масса альфа-частицы. При этом в результате распада конечное ядро и альфа-частица приобретают суммарную кинетическую энергию
Qa = ( M(A,Z) - M(A-4,Z-2) - Ma ) с2, (18)
которая называется энергией альфа-распада. Ядра могут испытывать альфа-распад также на возбужденные состояния конечных ядер и из возбужденных состояний начальных ядер. Поэтому соотношение для энергии альфа-распада (18) можно обобщить следующим образом
Qa = ( M(A,Z) - M(A-4,Z-2) - Ma ) с2 + 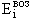 -
- 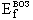 , (19)
, (19)
где 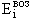 и
и 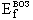 - энергии возбуждения начального и конечного ядер соответственно. Альфа-частицы, возникающие в результате распада возбужденных состояний, получили название длиннопробежных.
- энергии возбуждения начального и конечного ядер соответственно. Альфа-частицы, возникающие в результате распада возбужденных состояний, получили название длиннопробежных.
Основную часть энергии альфа-распада (около 98%) уносят альфа-частицы. Используя законы сохранения энергии и импульса для кинетической энергии альфа-частицы Ta можно получить соотношение
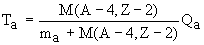 (20)
(20)
Периоды полураспада известных альфа-радиоактивных нуклидов варьируются от 0.298 мкс для 212Po до >1015 лет для 144Nd, 174Hf... Энергия альфа-частиц, испускаемых тяжелыми ядрами из основных состояний, составляет 4 - 9 МэВ, ядрами редкоземельных элементов 2 - 4.5 МэВ.
Важным свойством альфа-распада является то, что при небольшом изменении энергии альфа-частиц периоды полураспада меняются на многие порядки. Так у 232Th Qa = 4.08 МэВ, T1/2 = 1.41·1010 лет, а у 218Th Qa = 9.85 МэВ, T1/2 = 10 мкс. Изменению энергии в 2 раза соответствует изменение в периоде полураспада на 24 порядка.
Основные особенности альфа-распада, в частности сильную зависимость вероятности альфа-распада от энергии удалось в 1928 г. объяснить Г. Гамову и независимо от него Р. Герни и Э. Кондону. Ими было показано, что вероятность альфа-распада в основном определяется вероятностью прохождения альфа-частицы сквозь потенциальный барьер.
Рассмотрим простую модель альфа-распада. Предполагается, что альфа-частица движется в сферической области радиуса R, где R - радиус ядра. Т.е. в этой модели предполагается, что альфа-частица постоянно существует в ядре.
Вероятность альфа-распада  равна произведению вероятности найти альфа-частицу на границе ядра f на вероятность ee прохождения через потенциальный барьер D (прозрачность барьера)
равна произведению вероятности найти альфа-частицу на границе ядра f на вероятность ee прохождения через потенциальный барьер D (прозрачность барьера)
 = fD = ln2/T1/2 . (21)
= fD = ln2/T1/2 . (21)
Можно отожествить f с числом соударений в единицу времени, которые испытывает альфа-частица о внутренние границы барьера, тогда
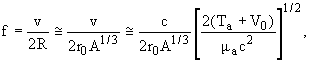 (22)
(22)
где v, Ta, 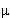 a - скорость внутри ядра, кинетическая энергия и приведенная масса альфа-частицы, V0 - ядерный потенциал. Подставив в выражение (22) V0 = 35 МэВ, Ta = 5 МэВ, получим для ядер с A
a - скорость внутри ядра, кинетическая энергия и приведенная масса альфа-частицы, V0 - ядерный потенциал. Подставив в выражение (22) V0 = 35 МэВ, Ta = 5 МэВ, получим для ядер с A 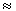 200, f
200, f 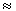 1021 с-1.
1021 с-1.
Hа рис. показана зависимость потенциальной энергии между альфа-частицей и остаточным ядром от расстояния между их центрами. Кулоновский потенциал обрезается на расстоянии R, которое приблизительно равно радиусу остаточного ядра. Высота кулоновского барьера Bk определяется соотношением
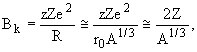 МэВ (23)
МэВ (23)
Здесь Z и z - заряды (в единицах заряда электрона e) остаточного ядра и альфа-частицы соответственно. Например для 238U Bk 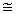 30 МэВ.
30 МэВ.
Можно выделить три области.
| 1. r < R - сферическая потенциальная яма глубиной V. В классической механике альфа-частица с кинетической энергией Ea+ V0 может двигаться в этой области, но не способна ее покинуть. В этой области существенно сильное взаимодействие между альфа-частицей и остаточным ядром. 2. R < r < re - область потенциального барьера, в которой потенциальная энергия больше энергии альфа-частицы, т.е. это область запрещенная для классической частицы. 3. r > re - область вне потенциального барьера. В квантовой механике возможно прохождение альфа-частицы сквозь барьер (туннелирование), однако вероятность этого весьма мала. | 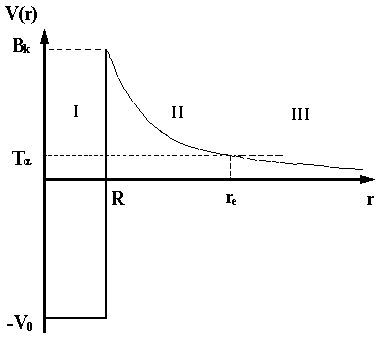
|
(Аналогично влияние кулоновского барьера и в случае ядерной реакции, когда альфа-частица подлетает к ядру. Если ее энергия меньше высоты кулоновского барьера, она скорее всего рассеется кулоновским полем ядра, не проникнув в него и не вызвав ядерной реакции. Вероятность таких подбарьерных реакций очень мала.)
Квантово-механическое решение задачи о прохождении частицы через потенциальный барьер дает для вероятности прохождения (коэффициента прозрачности барьера) D
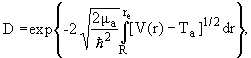 (24)
(24)
где 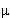 a- приведенная масса, Ta - энергия
a- приведенная масса, Ta - энергия  -частицы. В приближении Ta << Bk, где Bk - высота кулоновского барьера (предполагается, что барьер чисто кулоновский) описывается соотношением
-частицы. В приближении Ta << Bk, где Bk - высота кулоновского барьера (предполагается, что барьер чисто кулоновский) описывается соотношением
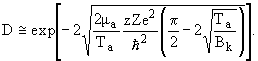 (25)
(25)
Рассчитанные периоды полураспада правильно передают важнейшую закономерность альфа-распада - сильную зависимость периода полураспадаT1/2 от энергии альфа-частиц Ta (энергии альфа-распада Qa 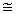 Ta ). При изменении периодов полураспада более чем на 20 порядков отличия экспериментальных значений от расчетных всего 1-2 порядка. Конечно, такие расхождения все же довольно велики. Где их источник и как надо усовершенствовать теорию, чтобы эти расхождения с экспериментом уменьшить? Какие факторы должны быть дополнительно учтены?
Ta ). При изменении периодов полураспада более чем на 20 порядков отличия экспериментальных значений от расчетных всего 1-2 порядка. Конечно, такие расхождения все же довольно велики. Где их источник и как надо усовершенствовать теорию, чтобы эти расхождения с экспериментом уменьшить? Какие факторы должны быть дополнительно учтены?
1. Приведенные выше формулы описывают эмиссию альфа-частиц с нулевым орбитальным моментом l. Однако возможен распад и с ненулевым орбитальным моментом, более того, в ряде случаев распад с l = 0 запрещен законами сохранения. В этом случае к кулоновскому Vk(r)добавляется центробежный потенциал Vц(r)
V(r) = Vk (r) + Vц (r),
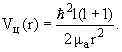
2.
2 Хотя высота центробежного барьера для тяжелых ядер при l = 8 составляет всего около 10% при от высоты кулоновского барьера и центробежный потенциал спадает быстрее, чем кулоновский, эффект вполне ощутим и для больших l может приводить к подавлению альфа-распада более, чем на 2 порядка.
3. Результаты расчетов прозрачности барьера весьма чувствительны к средним радиусам ядер R. Так изменение R всего на 4% приводит к изменению T1/2 в 5 раз. Между тем, ядра с A > 230 могут быть сильно деформированы, что приводит к тому, что альфа-частицы охотнее вылетают вдоль большой оси эллипсоида, а средняя вероятность вылета отличается от таковой для сферического ядра. Большую чувствительность периодов полураспада от радиусов можно использовать, определяя радиусы ядер по экспериментальным значениям периодов полураспада.
4. Выше никак не учитывалась структура состояний начального и конечного ядер и тесно связанная с этим проблема образования альфа-частицы в ядре, вероятность которой молчаливо полагалась равной 1. Для четно-четных ядер это приближение довольно хорошо описывает эксперимент. Однако, если перестройка структуры исходных ядер в конечные заметно затруднена, то необходимые для учета этих эффектов модификации предэкспоненциального множителя f, могут приводить к изменению расчетных значений приблизительно на два порядка.
Бета -распад
Бета-распад - спонтанное превращение ядра (A,Z) в ядро-изобар (A,Z+1) в результате испускания лептонов (электрон и антинейтрино, позитрон и нейтрино), либо поглощения электрона с испусканием нейтрино (е-захват).
В процессе 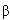 -распада выделяется энергия
-распада выделяется энергия
| Qб- = [Mя(A,Z) - Mя(A,Z+1) - me]c2 | - 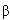 --распад, --распад,
|
| Qб+ = [Mя(A,Z) - Mя(A,Z-1) - me]c2 | - 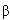 +-распад, +-распад,
|
| Qе-з = [Mя(A,Z) + me - Mя(A,Z-1)]c2 | - е-захват, |
где Mя - массы ядер, me - масса электрона. Так как табулируются массы или избытки масс атомов, то для энергий бета-распадов можно записать
| Qб- = [Mат(A,Z) - Mат(A,Z+1)]c2 | - 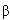 --распад, --распад,
|
| Qб+ = [Mат(A,Z) - Mат(A,Z-1)]c2 - 2mec2 | - 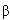 +-распад, +-распад,
|
| Qе-з = [Mат(A,Z) - Mат(A,Z-1)]c2 | - е-захват, |
где Mат - массы атомов. (Здесь мы пренебрегли разностью энергий связи электронов в начальном и конечном атомах.) Выделяющуюся в результате 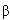 -распада энергию в основном уносят легкие частицы - лептоны (электрон, электронное антинейтрино, позитрон, электронное нейтрино).
-распада энергию в основном уносят легкие частицы - лептоны (электрон, электронное антинейтрино, позитрон, электронное нейтрино).
Энергии 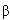 -распада варьируются от 0.02 МэВ
-распада варьируются от 0.02 МэВ
3H 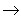 3He + e- +
3He + e- + 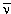 e + 0.02 МэВ
e + 0.02 МэВ
до ~20 МэВ
11Li 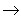 11Be + e- +
11Be + e- + 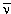 e + 20.4 МэВ
e + 20.4 МэВ
Периоды полураспада также изменяются в широком диапазоне от 10-3 с до 1016 лет. Большие времена жизни 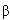 -радиоактивных ядер объясняются тем, что
-радиоактивных ядер объясняются тем, что 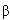 -распад происходит в результате слабого взаимодействия.
-распад происходит в результате слабого взаимодействия.
Ядра, испытывающие  -распад, расположены по всей периодической системе элементов. Из формулы Вайцзеккера для энергии связи ядра
-распад, расположены по всей периодической системе элементов. Из формулы Вайцзеккера для энергии связи ядра
Eсв(A,Z) = a1A - a2A2/3 - a3Z2/A1/3 - a4(A/2 - Z)2/A + a5A-3/4, (26)
учитывая, что от Z в основном зависят кулоновская энергия и энергия спаривания, можно получить равновесное число протонов в ядре (при фиксированном A), которое определяется максимумом энергии связи.
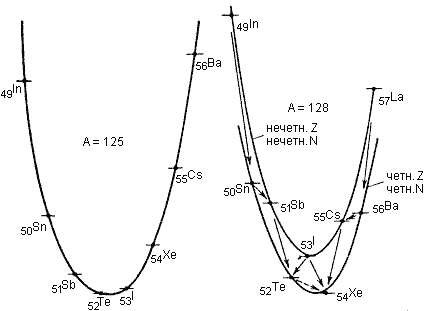 Параболы масс для ядер с нечетным A, и с четным A (нечетно-нечетных и четно-четных ядер) Параболы масс для ядер с нечетным A, и с четным A (нечетно-нечетных и четно-четных ядер)
|
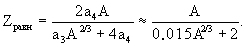
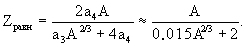 (27)
(27)
Т. к. A = N + Z, формула (27) определяет соотношение между числом протонов Z и нейтронов N для ядер долины стабильности. При Z < Zравн ядро нестабильно к 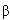 --распаду, а при Z > Zравн к
--распаду, а при Z > Zравн к 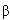 +-распаду и E-захвату. При всех A
+-распаду и E-захвату. При всех A 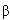 -стабильные ядра должны группироваться вокруг значений Zравн. Из (2) видно, что при малых A Zравн ~ A/2 т. е. стабильные легкие ядра должны иметь примерно одинаковое количество протонов и нейтронов (роль кулоновской энергии мала). С ростом A роль кулоновской энергии увеличивается и количество нейтронов в устойчивых ядрах начинает превышать количество протонов. На левой части рис.1 показаны парабола масс для ядер с нечетным A = 125. Стабильное ядро 125Te находится в минимуме массовой параболы (соответственно в максимуме параболы для энергии связи). 125In, 125Sn, 125Sb подвержены
-стабильные ядра должны группироваться вокруг значений Zравн. Из (2) видно, что при малых A Zравн ~ A/2 т. е. стабильные легкие ядра должны иметь примерно одинаковое количество протонов и нейтронов (роль кулоновской энергии мала). С ростом A роль кулоновской энергии увеличивается и количество нейтронов в устойчивых ядрах начинает превышать количество протонов. На левой части рис.1 показаны парабола масс для ядер с нечетным A = 125. Стабильное ядро 125Te находится в минимуме массовой параболы (соответственно в максимуме параболы для энергии связи). 125In, 125Sn, 125Sb подвержены 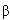 --распаду, 125I, 125Xe, 125Cs, 125Ba -
--распаду, 125I, 125Xe, 125Cs, 125Ba - 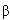 +-распаду. Чем больше энергия бета-распада ядер (разность масс между соседними изобарами), тем они дальше от линии стабильности.
+-распаду. Чем больше энергия бета-распада ядер (разность масс между соседними изобарами), тем они дальше от линии стабильности.
Для четных A вместо одной параболы, за счет энергии спаривания (последний член в формуле (26)), получаются две параболы (правая часть рис.1): для нечетно-нечетных ядер и для четно-четных. Несмотря на то, что энергия спаривания невелика по сравнению с полной энергией связи ядра (для ядер с A ~ 100 энергия связи порядка 1000 МэВ, расстояние между параболами около 2 МэВ), это приводит к важным следствиям. Некоторые нечетно-нечетные ядра (например 128I) могут испытывать как 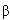 --распад, так и
--распад, так и 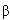 +-распад и e-захват. Стабильных четно-четных ядер значительно больше, чем стабильных ядер с нечетным A и, тем более, чем стабильных нечетно-нечетных ядер, которых всего четыре (2H, 6Li, 10B, 14N ). При данном A стабильных четно-четных ядер может быть несколько (например 136Xe, 136Ba, 136Ce). Элементы с нечетным Z редко имеют больше одного стабильного изотопа, в то время как для элементов с четным Z это не редкость (112Sn, 114Sn, 115Sn, 116Sn, 117Sn, 118Sn, 119Sn, 120Sn, 122Sn, 124Sn). В некоторых случаях, когда для четно-четных ядер невозможен бета-распад на нечетно-нечетное ядро, оказывается энергетически возможным переход с изменением Z на две единицы - двойной бета-распад. Такой экзотический распад испытывают 128Te и 130Te. Их содержание в естественной смеси этого элемента 31.7% и 33.8% соответственно. Вероятность двойного бета-распада очень мала, периоды полураспада T1/2(128Te) = 7.7*1028 лет, T1/2(130Te) = 2.7*1021 лет.
+-распад и e-захват. Стабильных четно-четных ядер значительно больше, чем стабильных ядер с нечетным A и, тем более, чем стабильных нечетно-нечетных ядер, которых всего четыре (2H, 6Li, 10B, 14N ). При данном A стабильных четно-четных ядер может быть несколько (например 136Xe, 136Ba, 136Ce). Элементы с нечетным Z редко имеют больше одного стабильного изотопа, в то время как для элементов с четным Z это не редкость (112Sn, 114Sn, 115Sn, 116Sn, 117Sn, 118Sn, 119Sn, 120Sn, 122Sn, 124Sn). В некоторых случаях, когда для четно-четных ядер невозможен бета-распад на нечетно-нечетное ядро, оказывается энергетически возможным переход с изменением Z на две единицы - двойной бета-распад. Такой экзотический распад испытывают 128Te и 130Te. Их содержание в естественной смеси этого элемента 31.7% и 33.8% соответственно. Вероятность двойного бета-распада очень мала, периоды полураспада T1/2(128Te) = 7.7*1028 лет, T1/2(130Te) = 2.7*1021 лет.
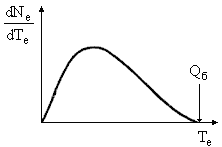 Рис. 2. Схематический вид спектра электронов (позитронов при бета-распаде Рис. 2. Схематический вид спектра электронов (позитронов при бета-распаде
|
В результате бета-распада образуются три частицы: конечное ядро и пара лептонов. Энергия, сообщаемая ядру в силу его большой массы, мала, и ею можно пренебречь. Поэтому кинетическая энергия, выделяющаяся при бета-распаде практически целиком уносится парой лептонов, причем распределение энергий между ними может быть любым. Таким образом, энергетический спектр позитронов (электронов) и нейтрино (антинейтрино) должен быть непрерывным в интервале от 0 до Qб (см. рис. 2).
В случае захвата ядром орбитального электрона образуются два продукта: конечное ядро и нейтрино. Распределение энергий между ними поэтому является однозначным, и практически вся она уносится нейтрино. Таким образом, спектр нейтрино при e-захвате при фиксированных состояниях начального и конечного ядра будет монохроматическим в отличие от бета-распада. В e-захвате участвуют главным образом электроны ближайших, к ядру оболочек (прежде всего К-оболочки) Для таких электронов вероятность нахождения внутри ядра наибольшая.
Характерной чертой всех видов бета-распада является участие в них нейтрино или антинейтрино. Впервые гипотеза о существовании нейтрино была выдвинута Паули в 1930 г. для "спасения" законов сохранения энергии и момента количества движения. Непрерывный характер спектра электронов (позитронов) никак не удавалось объяснить без отказа от закона сохранения энергии. Гипотеза нейтрино позволила не отказаться от столь фундаментального принципа. Прошли многие годы, пока Коуэну и Райнесу удалось зафиксировать электронное антинейтрино.
 Диаграмма Фейнмана для Диаграмма Фейнмана для 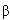 --распада --распада
|
Бета-распад происходит в результате слабых взаимодействий. На рис. показана диаграмма Фейнмана для 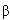 --распада. На кварковом уровне при бета-распаде происходит переход d-кварка в u-кварк или наоборот. На нуклонном уровне это соответствует переходам нейтрона в протон или протона в нейтрон. Причем если нейтрон может переходить в протон в свободном состоянии, то обратный переход возможен только для протонов в ядре.
--распада. На кварковом уровне при бета-распаде происходит переход d-кварка в u-кварк или наоборот. На нуклонном уровне это соответствует переходам нейтрона в протон или протона в нейтрон. Причем если нейтрон может переходить в протон в свободном состоянии, то обратный переход возможен только для протонов в ядре.
Бета-распады разделяются на разрешенные и запрещенные, различающиеся вероятностями переходов. К разрешенным переходам относятся переходы, при которых суммарный орбитальный момент l, уносимый электроном и нейтрино, равен нулю. Запрещенные переходы подразделяются по порядку запрета, который определяется орбитальным моментом l. Если l = 1, то это запрещенный переход первого порядка, lmin = 2 - второго порядка и т.д. При прочих равных условиях отношения вероятностей вылета частицы с орбитальными моментами l = 0 (w0) и l  0 (wl)
0 (wl)
wl/w0 ~ (R/ 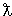 )2l, (28)
)2l, (28)
Дата добавления: 2015-11-06; просмотров: 4580;
