Лекция 17. Проводимость полупроводников.
При повышении температуры полупроводника электроны, «задействованные» в ковалентных связях между атомами кристаллической решетки, получают дополнительную энергию и могут перейти в свободное состояние, т.е. стать носителями заряда и участвовать в проводимости. Минимально необходимая для этого энергия DW называется энергией активации полупроводника.
В чистых полупроводниках, состоящих из атомов одного химического элемента, электроны переходят из валентной зоны ВЗ (рис. 44) в свободную зону СЗ (которая в этом случае становится зоной проводимости ЗП). При этом электроны должны преодолеть энергетический барьер DW, равный ширине запрещенной зоны ЗЗ. Освободившаяся «вакансия» в ковалентной связи – так называемая дырка – может быть занята электроном из соседней связи и т.д. Под действием электрического поля дырка будет вести себя как положительный носитель заряда и также участвовать в проводимости. Таким образом, в чистом полупроводнике проводимость в равной степени осуществляется как отрицательными носителями – свободными электронами, так и положительными – дырками. Из приведенных выше рассуждений следует, что концентрации свободных электронов nэ в свободной зоне и дырок nд в валентной зоне в таком полупроводнике одинаковы: nэ = nд .
 Как известно, внутри кристалла концентрация электронов, обладающих энергией W, определяется на основе распределения Ферми-Дирака
Как известно, внутри кристалла концентрация электронов, обладающих энергией W, определяется на основе распределения Ферми-Дирака
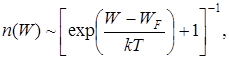 (1)
(1)
где WF – энергия Ферми; k – постоянная Больцмана; Т – абсолютная температура. В чистых полупроводниках уровень Ферми WF расположен посередине запрещенной зоны ЗЗ (см. рис. 44); поэтому для электронов, перешедших в зону проводимости, разность W - WF = 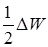 . При температурах до тысячи кельвин произведение kT не превышает 0,1 эВ, в то время как ширина запрещенной зоны составляет несколько десятых эВ, – следовательно, единицей в квадратных скобках выражения (1) можно пренебречь про сравнению с экспоненциальным слагаемым и распределение Ферми переходит в классическое распределение Больцмана:
. При температурах до тысячи кельвин произведение kT не превышает 0,1 эВ, в то время как ширина запрещенной зоны составляет несколько десятых эВ, – следовательно, единицей в квадратных скобках выражения (1) можно пренебречь про сравнению с экспоненциальным слагаемым и распределение Ферми переходит в классическое распределение Больцмана:
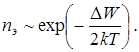 (2)
(2)
Так как электропроводность вещества s прямо пропорциональна концентрации носителей заряда (s ~ nэ ), а его электрическое сопротивление R в свою очередь обратно пропорционально электропроводности ( 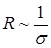 ), с учетом (2) можно представить температурную зависимость сопротивления полупроводника в виде
), с учетом (2) можно представить температурную зависимость сопротивления полупроводника в виде
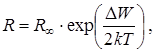 (3)
(3)
где величина R¥ характеризует сопротивление при бесконечно высокой температуре.
Аналогичные закономерности справедливы и для примесной проводимости полупроводников. В полупроводниках n-типа валентность примеси (донора) на единицу превышает валентность основного вещества. Поэтому «лишние» валентные электроны особенно легко переходят в свободное состояние без образования дырки в валентной зоне (рис. 45, а).

Рис. 45
Для таких полупроводников nэ >> nд (электроны являются основными, а дырки – неосновными носителями). Уровни донорной примеси располагаются вблизи «дна» свободной зоны, и энергия активации примеси DW значительно меньше ширины запрещенной зоны.
В полупроводниках р-типа валентность примеси (акцептора) на единицу меньше, чем у атомов основного вещества. «Лишняя» вакансия в ковалентной связи атома примеси легко превращается в дырку без предварительного перехода электронов в свободную зону (рис. 45, б); в таких полупроводниках основными носителями являются дырки. А неосновными – свободные электроны (nэ << nд). Уровни акцепторной примеси лежат вблизи «потолка» валентной зоны, которая становится зоной проводимости, и энергия активации DW при этом также меньше ширины запрещенной зоны.
При высоких температурах практически все донорные уровни освобождаются, а акцепторные – занимаются электронами; таким образом, исчерпывается механизм примесной проводимости. Дальнейшее повышение температуры все больше способствует переходам электронов из валентной зоны в свободную, как это имеет место в чистых полупроводниках (собственная проводимость).
Итак, независимо от наличия и характера примеси, на сопротивление полупроводников весьма существенно влияет их температура. Зависимость R(T) принято характеризовать термическим коэффициентом сопротивления a , представляющим собой относительное изменение сопротивления при изменении температуры на один кельвин:
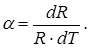 (4)
(4)
Подставляя в (4) зависимость (3), получим:
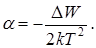
Таким образом, в отличие от металла, у полупроводника термический коэффициент сопротивления, во-первых, отрицателен, во-вторых, не является постоянным (зависит от температуры). Это говорит о том, что сопротивление полупроводника уменьшается с ростом температуры, причем не по линейному закону.
Сам факт явно выраженной температурной зависимости сопротивления позволяет использовать ПТС в качестве датчика температуры, т.е. определять его температуру по измеренному сопротивлению.
СОДЕРЖАНИЕ
| № лекции | Содержание лекции | Страница |
| 1. | Квантово-оптические явления. Тепловое излучение | |
| 2. | Фотоэффект | |
| 3. | Давление света. Эффект Комптона | |
| 4. | Спектры атомов. Атомная физика. Теория Бора | |
| 5. | Рентгеновское излучение | |
| 6. | Элементы квантовой механики. Волновая функция. Уравнение Шредингера для свободной частицы | |
| 7. | Длина волны де Бройля. Волновые пакеты. Соотношения неопределенностей. | |
| 8. | Стационарные состояния. Прохождение частицы через потенциальный барьер. Туннельный эффект. | |
| 9. | Связанные состояния. Частица в потенциальном ящике | |
| 10. | Принцип действия лазера | |
| 11. | Молекулярные спектры | |
| 12. | Ядерная физика. Строение атомного ядра. Ядерные силы. Размер и плотность ядра | |
| 13. | Энергия связи и масса ядра | |
| 14. | Радиоактивность. Закон радиоактивного распада | |
| 15. | Виды радиоактивного распада | |
| 16. | Ядерные реакции | |
| 17. | Проводимость полупроводников |
2) Соорудить поток электронов вполне возможно: в телевизионной трубке, в электронной пушке, электроны излучаются из раскалённой нити, ускоряются электрическим полем, луч формируется, и на экране рисует картину.
3) Вместо пучка электронов можно представить поток пуль из пулемёта, щит броневой со щелью, а дальше деревянный забор регистрирует попадания пуль, понятно, что они будут рассеиваться, проходя через эту щель.
1) На рис.1.c точка отмечена крестиком
1) Так сказать, пока частица не обнаружилась где-то, Господь Бог, понимая под этим существо, которое знает всё, что можно знать, он не знает, где она будет обнаружена, он тоже может оперировать только вероятностью. В рамках этой же метафоры Господь Бог-то знает, где молекулы воздуха летают, это мы не знаем, но он знает, потому что, в принципе, можно за ними следить и можно знать, где какая из них. А где будет обнаружена частица, описываемая волновой функцией, это и Господь Бог не знает. Вот такая ситуация. Разные аспекты этого дела ещё проявятся более занимательным образом.
1) Почему мы считаем, что уравнения Максвелла справедливы? Потому что работает теория: радиоприёмники говорят, телевизоры картинку показывают, и, вообще, всё, что называется электричеством, железно из этих уравнений следует.
1) В чём состоит функционирование физика? Он должен уметь слова обычного языка переводить в какие-то математические формулы, вот и всё. Допустим, человек обычным языком описывает проблему, а специалист должен будет потом, зная законы природы, сказать, что будет. Так вот, специалист должен будет перевести эту, может быть, и несвязанную речь на язык математики. На этом функция физика кончается, потому что, как только он перевёл, он может пойти к знакомому математику и дать ему математическую проблему и сказать, вот решай. Математик его не будет спрашивать, что такое буква Ψ, буква t, математику важно знать, что это некоторая функция от переменных x, y, z, ему не надо знать, что эти переменные представляют. Математик это всё продолбит и даст решение, не понимая, что всё это означает. Дальше, опять физик может это проинтерпретировать. Значит, физик работает только на стадии перевода. Но такого разделения труда между физиками и математиками нет, и физикам всегда приходится работать по совместительству математиками, более того, математика в XVIII, XIX веке развивалась в основном физиками, потому что проблемы брались из физики. Вклад чистых математиков в эту науку оказался удивительным, и при случае, если не забуду, я об этом поговорю.
2) Чем замечательны экспоненты – их дифференцировать приятно.
3) Есть рецепт дивергенции от произведения скалярной функции на вектор: 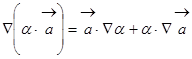 , так как
, так как 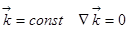 .
.
1) Луи де Бройль, кстати, недавно умер, хотя это придумал в 20-х годах. Он из королевской семьи, это один из последних Бурбонов.
1) В классической физике тоже понималось, что, когда мы наблюдаем объект, то мы с ним взаимодействуем: надо объект осветить и смотреть, по крайней мере, отражённый свет. Но в классической физике считалось, что это взаимодействие можно сделать настолько малым, что оно не меняет состояния объекта, но это оказалось большим заблуждением: в области атомных масштабов наблюдение нельзя сделать таким, чтобы оно не меняло состояния объекта. Наблюдение само по себе это вовсе не невинное дело: когда мы взаимодействуем с объектом в атомных масштабах, его состояние меняется.
2) Мы обсуждали в своё время разрешающую способность оптических инструментов, к сожалению, на экзамене я убедился, что многие эту вещь проигнорировали. Совершенно дифракционное явление: в микроскоп мы можем разрешить две близкие точки, то есть воспринять их как две различные точки, если расстояние между ними не меньше длины волны. Длина волны света, который используется в микроскопе, определяет разрешающую способность.
1) Любая реальная волна, согласно теореме Фурье, может быть представлена как суперпозиция монохроматических волн с различными амплитудами и частотами ω в некотором интервале Δω. Суперпозицию волн, мало отличающихся друг от друга по частотам 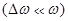 , называют волновым пакетом или группой волн. //И.Е. Иродов. Волновые процессы. М.1999. стр. 223.
, называют волновым пакетом или группой волн. //И.Е. Иродов. Волновые процессы. М.1999. стр. 223.
2) Простейший наглядный пример – звуковая волна. Кто-нибудь издаст сейчас кратковременный вопль, и побежит звуковая волна длиной 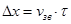 , где τ – длительность вопля. Кстати, если длительность вопля полсекунды, то длина этого пакета будет 150м. И побежит такое возмущение длиной 150м, оно, конечно, не монохроматическое, там уже появится целый спектр частот, и чем кратковременнее вопль, тем больший набор частот требуется для этого.
, где τ – длительность вопля. Кстати, если длительность вопля полсекунды, то длина этого пакета будет 150м. И побежит такое возмущение длиной 150м, оно, конечно, не монохроматическое, там уже появится целый спектр частот, и чем кратковременнее вопль, тем больший набор частот требуется для этого.
1) Поясним эту формулу на примере суперпозиции двух волн с одинаковой амплитудой и несколько отличными друг от друга длинами волн (и частотами). На рис.3.2, а показано их относительное расположение в некоторый момент времени, а на рис.3.2, б – результат их суперпозиции. Нас будет интересовать скорость, с которой перемещается место с максимальной амплитудой – это и будет скорость волнового пакета – групповая скорость.
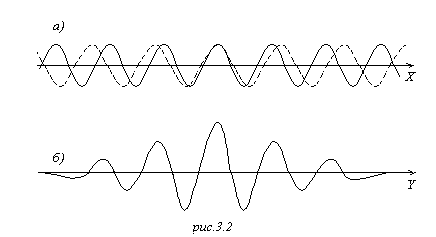
//И.Е. Иродов. Волновые процессы. М.1999. стр.224.
1) Наглядный пример. Приходилось, наверное, наблюдать забеги на длинные дистанции. Вот группа бегунов стартует, эта компактная куча начинает бежать. Отдельный бегун – это отдельная синусоидальная составляющая. Потом, поскольку бегуны все разные, бегут с разными скоростями, это начинает размазываться: сначала бегут компактной группой, потом эта группа разбивается, потом, вообще, оказывается, один на круг отстаёт, и всё начинает путаться. Вот расплывание пакета.
2) Теперь понятно, почему существует классическая механика, почему она оказалась правильной. Например, масса пули m=10-2, допустим центр масс пули был локализован в интервале Δx0=10-5м. На сколько увеличится неопределённость в координате пули за какое-то время? Δx~10-27t. За сутки полёта пули (t=10-5) мы получим Δx~10-22. 10-10 – размер атома водорода. Потому-то пули и летают как компактные объекты, потому что у них масса достаточная, потому и справедлива классическая механика. Если мы в формулу подставим массу электрона me~10-30, то мы видим, что для электрона волновой пакет мгновенно расплывается, и его координата сразу теряется через относительно короткое время.
1) Можно жидкость, например, нагреть в обычных условиях до температуры выше 100о, и она не будит кипеть, если греть очень чистую жидкость без всяких примесей, греть осторожно. Кстати, если потом эту кастрюлю с такой жидкостью немножко тряхнуть, она взрывается, она мгновенно испаряется. Точно так же можно аккуратно охлаждать водяной пар в чистом воздухе до состояния с температурами ниже той, при которой он должен был бы сконденсироваться и превратиться в воду и даже в лёд.
1) Понятно, что вовсе не всякая функция представляется в таком виде, скажем, не всякая функция f(x, y) представляется в виде g(x)h(y), поэтому, если мы найдём такие решения, то это будут какие-то специальные решения.
1) Немедленно вопрос может возникнуть, почему планеты вращаются вокруг Солнца? Мы детально не обсуждали, как выглядит настоящая полевая теория для гравитационного поля, но, когда Земля вращается вокруг Солнца, то поле должно меняться синхронно, а поскольку синхронно меняться не может, то должны излучаться гравитационные волны. Почему тогда Земля не падает на Солнце? Ответ простой – мощность мала. Волны излучается, энергия уносится, но гравитационное взаимодействие примерно на 40 порядков слабее электромагнитного, это самое слабое взаимодействие. Энергия уносимая волнами просто очень мала, и, скажем, Земля за 4 млрд. лет, сколько она существует, сделала 4 млрд. оборотов, но приблизилась к Солнцу ничтожно мало.
1) Если кинетическая энергия электрона меньше, чем работа по преодолению тормозящего поля, то налетающий электрон внутри останавливается и выбрасывается обратно. Это по здравым представлениям, ну, и по классической физике. Посмотрим, что даёт наша теория.
2) Непрерывность гарантирует, что вероятность не прыгает резко при малом смещении, то есть вероятность меняется непрерывно.
1) Вот, кстати, на счёт предела в рекордах. Вы, наверное, анализ изучали, там сказано, что всякая монотонная ограниченная последовательность имеет предел. Когда я был на вашем месте, как только услыхал такую теорему, меня пронзило – это означает, что любые рекорды имеют предел. Рост рекордов в прыжках, в беге это заведомо ограниченная последовательность, стало быть, есть предел, то есть когда-то все эти спортивные соревнования упрутся в смысле рекордов. Конечно, прыгать можно всегда, потому что это личные соревнования, но рекорды расти перестанут. Такая вот эта теорема.
2) Если бы человек выскочил из ямы, так сказать, прыгнул выше головы, то нарушился бы закон сохранения энергии (у него нет энергии, чтобы подскочить на 3м). Но если он оказывается за стеной, его энергия в начальном состоянии и в конечном одна и та же, просто произошло действие, несколько запрещённое с точки зрения классической физики было туннельного, но нарушения закона сохранения энергии нет.
3) Если бы не эффекта, то с электричеством было бы не так просто. Это означает, что вы должны были бы, например, провода, ведущие к вашему чайнику, впаять в него, а другие два конца привести на электростанцию и впаять туда, чтобы было сплошное металлическое тело. Просто при механическом контакте ток не потёк бы, если б не было туннельного эффекта.
1) Земля, движущаяся вокруг солнца, находится в связанном состоянии, камни, которые мы на земле можем наблюдать, - в связанном состоянии (они не могут уйти на бесконечность). В этом смысле все окружающие нас объекты в пределах солнечной системы это частицы в связанном состоянии. Единственные объекты, которые отражают несвязанные состояния, это два американских аппарата, которые были запущены лет пятнадцать назад
2) Когда переменная принимает определённые значения (счётное множество дискретных значений), говорят, что эта переменная квантуется.
3) Строго говоря, если быть очень аккуратным, при измерении энергии могут быть получены лишь определённые значения. Это важный нюанс. Квантовая теория не считает, что объект обладает какой-то характеристикой сам по себе, пока мы не пытаемся её измерить. Вот когда мы измеряем ту или иную характеристику, она появляется. Этому есть экспериментальное подтверждение. Если объект имеет сам по себе какие-то характеристики, то можно привести примеры, когда в определённых ситуациях будут получаться определённые следствия, а если он не обладает сам по себе, тогда следствия в тех же ситуациях будут другими. Это положение теории, очень интригующее, неоднократно проверялось – если мы будем считать, что система обладает сама по себе какой-то характеристикой, то из этого можно получить следствия, противоречащие наблюдаемому в действительности. Значит, при измерении энергии могут быть получены лишь определённые значения.
1) Вот сейчас кто-нибудь снаружи дверь закроет на ключ, и мы все в связанном состоянии. И будем рассматривать нас тут сейчас с точки зрения квантовой теории.
[a] Кирхгоф Густав Роберт (1824-1887) – нем. физик, иностранный член-корреспондент Петербургской АН (1862). Установил (1847) правила для электрической цепи, названные его именем. Совместно с Р.В. Бунзеном заложил основы спектрального анализа (1859), открыл цезий (1860) и рубидий (1861).ввел понятие абсолютно черного тела и открыл (1859) закон излучения, названный его именем. Труды по механике, математической физике.
[b] Стефан Йозеф (1835-1893) – австр. физик. Экспериментально установил (1879) закон излучения абсолютно черного тела (закон Стефана-Больцмана). Труды по диффузии, теплопроводности газов, оптике и др.
[c] Больцман Людвиг (1844-1906) – австр. физик, один из основателей статистической физики и физической кинетики. Иностранный член-корреспондент Петербургской АН (1899). Вывел функцию распределения, названную его именем, и основное кинетическое уравнение газов. Дал (1872) статистическое обоснование второго начала термодинамики. Вывел один из законов теплового излучения (закон Стефана-Больцмана).
[d] Вин Вильгельм (1864-1928) – нем. физик, Труды по теории излучения, оптике, термодинамике, физике газового разряда. Вывел (1893) законы излучения и смещения, названные его именем. Измерил длину рентгеновского излучения. Нобелевская премия (1911).
[e] Джинс Джеймс Хопвуд (1877-1946) – англ. физик и астрофизик. Основные труды по кинетической теории газов, теории теплового излучения, фигурам равновесия вращающихся жидких тел, строению и эволюции звезд, звездных систем и туманностей. Вывел (1905-1909 независимо от Дж. У. Рэлея) закон излучения (назван позднее законом Рэлея-Джинса).
[f] Столетов Александр Григорьевич (1839-1896) – физик. Получил кривую намагничивания железа (1872), систематически исследовал внешний фотоэффект (1888-1890), открыл первый закон фотоэффекта. Исследовал газовый разряд, критическое состояние и др. Основатель (1874) физической лаборатории в Московском университете.
[g] Герц Генрих Рудольф (1857-1894) – нем. физик, один из основоположников электродинамики. Экспериментально доказал (1886-1889) существование электромагнитных волн (используя вибратор Герца) и установил тождественность основных свойств электромагнитных и световых волн. Придал уравнениям Максвелла симметричную форму. Открыл внешний фотоэффект (1887).
[h] Лукирский Петр Иванович (1894-1954) – физик, академик АН СССР (1946). Один из основателей эмиссионной электроники. Труды по физике рентгеновских лучей и ядерной физике. Классические работы по фотоэффекту.
[i] Комптон Артур Холли (1892-1962) – амер. физик. Открыл и объяснил (1922) эффект, названный его именем и состоящий в упругом рассеянии электромагнитного излучения малых длин волн (рентгеновского и гамма-излучения) на свободных электронах, сопровождающемся увеличением длины волны. Обнаружил полное внутреннее отражение рентгеновских лучей. Открыл широтный эффект в космических лучах. Участник создания атомной бомбы. Нобелевская премия (1927).
Дата добавления: 2015-11-06; просмотров: 2564;
