Эффект Комптона[i].
Корпускулярные свойства света особенно отчетливо проявляются в явлении, которое получило название эффект Комптона.
В 1923г. А. Комптон, исследуя рассеяние рентгеновских лучей (фотонов большой энергии) различными веществами (в основном легкими: графитом, парафином и др.), содержащими свободные или слабо связанные электроны, обнаружил, что в рассеянных лучах, наряду с излучением первоначальной длины волны l содержатся также лучи с длиной волны l¢ большей l (l¢>l). Причем разность Dl=l¢-l оказалась независящей от l и от природы рассеивающего вещества, а целиком определялась углом рассеяния. Экспериментально была установлена следующая закономерность:
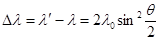 ,
,
где q - угол, образуемый направлением рассеянного излучения с направлением первичного пучка; l0 – постоянная для всех веществ величина, равная l0=0,0242 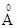 =2,42×10-12м.
=2,42×10-12м.
ОПРЕДЕЛЕНИЕ: рассеяние электромагнитного излучения на свободных или слабо связанных электрона, при котором отдельный фотон в результате упругого соударения с электроном передает ему часть своего импульса (часть энергии), называется эффектом или явлением Комптона.
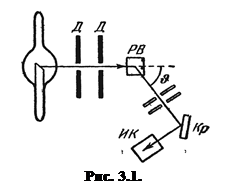
Схема опыта Комптона показана на рисунке 3.1. Монохроматическое (характеристическое) рентгеновское излучение, возникающее в рентгеновской трубке, проходит через диафрагмы Д и узким пучком направляется на легкое (графит, парафин и т.п.) рассеивающее вещество РВ. Спектральный состав рассеянного излучения исследуется с помощью рентгеновского спектрографа, состоящего из кристалла Кр и ионизирующей камеры ИК.

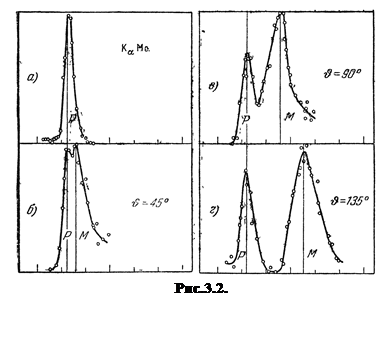 |
На рисунке 3.2. приведены результаты исследования рассеяния монохроматических рентгеновских лучей (линия KaMo) на графите. Кривая «а» характеризует первичное излучение. Остальные кривые относятся к различным углам рассеяния q, значения которых указаны на рисунке 3.2. По оси ординат отложена интенсивность излучения, по оси абсцисс – величина, пропорциональная длине волны.
Также экспериментально было установлено, что при рассеянии излучения веществами с малыми атомными номерами (Li, Be, B) практически все рассеянное излучение имеет смещенную длину волны. По мере увеличения атомного номера все большая часть излучения рассеивается без изменения длины волны.
Указанные особенности эффекта Комптона можно объяснить, рассматривая рассеяние как процесс упругого столкновения рентгеновских фотонов с практически свободными электронами. Полученные на опыте факты противоречат классической теории, согласно которой частота вынужденных колебаний должна точно совпадать с частотой вынуждающей силы, т.е. частотой облучающего света, и не может возникать никаких дополнительных спектральных составляющих в рассеянном излучении.
 По квантовой теории столкновение фотона со связанным электроном должно приводить к частичной потере энергии фотона, в результате чего квант после столкновения (
По квантовой теории столкновение фотона со связанным электроном должно приводить к частичной потере энергии фотона, в результате чего квант после столкновения ( 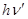 ) будет меньше исходного (
) будет меньше исходного ( 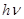 ). В зависимости от геометрии эксперимента соотношение между n и
). В зависимости от геометрии эксперимента соотношение между n и 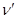 может изменяться, здесь n и
может изменяться, здесь n и 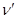 -частота падающего и рассеянного фотонов. Поскольку электрону отдачи (или его еще часто называют комптоновским электроном) передается энергия от падающего фотона, то длина волны рассеянного фотона должна быть больше длины падающего излучения.
-частота падающего и рассеянного фотонов. Поскольку электрону отдачи (или его еще часто называют комптоновским электроном) передается энергия от падающего фотона, то длина волны рассеянного фотона должна быть больше длины падающего излучения.
 Для количественной оценки рассматриваемого эффекта запишем законы сохранения энергии и импульса. Считаем, что до соударения электрон не двигался (т.е. его энергия равна m0c2, m0 – масса покоя электрона, импульс равен нулю). После столкновения электрон будет обладать энергией mc2 и импульсом
Для количественной оценки рассматриваемого эффекта запишем законы сохранения энергии и импульса. Считаем, что до соударения электрон не двигался (т.е. его энергия равна m0c2, m0 – масса покоя электрона, импульс равен нулю). После столкновения электрон будет обладать энергией mc2 и импульсом  . Энергию связи электрона в атоме не учитываем. Полагаем также, что энергия падающего фотона
. Энергию связи электрона в атоме не учитываем. Полагаем также, что энергия падающего фотона 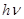 , а импульс равен
, а импульс равен 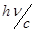 . Тогда
. Тогда
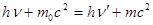 - закон сохранения энергии,
- закон сохранения энергии,
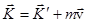 - закон сохранения импульса,
- закон сохранения импульса,
где 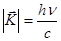 ,
, 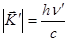 .
.
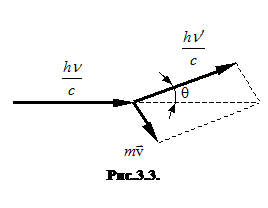
Для совместного решения этих двух уравнений воспользуемся рисунком 3.3., где изображены относительные направления всех трех интересующих нас векторов.
Разделим уравнение, описывающее закон сохранения энергии на «с», тогда получим:
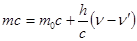 .
.
Возведем это уравнение в квадрат
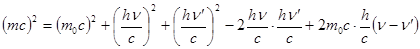 .
.
Из рисунка 3.3. следует, что
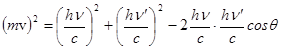 ,
,
где q - угол между направлением распространения рассеянного излучения и направлением первичного пучка.
Вычтя последнее уравнение из предпоследнего, получим
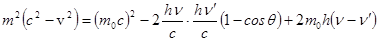 .
.
Учтя, что 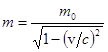 , можно показать, что
, можно показать, что 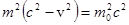 и тогда
и тогда
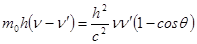 .
.
Разделив полученное соотношение на 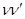 и учитывая, что
и учитывая, что 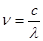 , получаем формулу
, получаем формулу
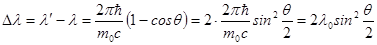 ,
,
совпадающую с эмпирической.
Анализ этой простой формулы показывает, что смещение возрастает с увеличением угла рассеяния, достигая максимума при q=p, т.е. в том случае, когда рассеянное излучение направлено навстречу возбуждающему.
Величина 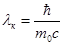 называется комптоновской длиной волны той частицы, масса которой имеется в виду. Для электрона lк.э.=3,86×10-11см=0,00386
называется комптоновской длиной волны той частицы, масса которой имеется в виду. Для электрона lк.э.=3,86×10-11см=0,00386 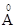 . Умножив lк.э. на 2p, получим для l0 значение 0,0242
. Умножив lк.э. на 2p, получим для l0 значение 0,0242 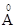 , совпадающее с эмпирическим значением.
, совпадающее с эмпирическим значением.
Проведенные вычисления не учитывали рассеяние рентгеновских лучей, взаимодействующих с сильно связанными в атоме электронами. Т.е. фактически исследовалось рассеяние на легких атомах, где связь очень слабая. В согласии с данными опыта в этом случае интенсивность смещенной компоненты относительно велика. По мере роста атомного номера увеличивается относительное число электронов с сильной связью и значительная часть фотонов как бы испытывает столкновение с атомом большой массы. Поэтому в спектре рассеяния будет велика интенсивность несмещенной компоненты.
Дата добавления: 2015-11-06; просмотров: 5243;
