Математическая модель задачи
Лекция 8. Транспортная задача линейного программирования
План:
1. Математическая модель задачи
2. Определение начального опорного плана задачи
Математическая модель задачи
Пусть имеется 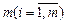 поставщиков (или пунктов отправления), располагающих некоторым однородным продуктом в объемах по
поставщиков (или пунктов отправления), располагающих некоторым однородным продуктом в объемах по 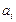 единиц, и
единиц, и 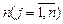 получателей (или пунктов назначения) с объемами потребления по
получателей (или пунктов назначения) с объемами потребления по 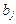 единиц. Задана матрица
единиц. Задана матрица 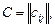 где
где  – стоимость перевозки единицы продукции от i-го поставщика j-му потребителю. Возникает задача определения плана перевозок
– стоимость перевозки единицы продукции от i-го поставщика j-му потребителю. Возникает задача определения плана перевозок 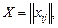 где
где 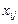 – количество единиц продукции, поставляемой по коммуникации (i, j), которая бы минимизировала суммарную стоимость всех перевозок. Математическая модель задачи будет иметь вид:
– количество единиц продукции, поставляемой по коммуникации (i, j), которая бы минимизировала суммарную стоимость всех перевозок. Математическая модель задачи будет иметь вид:
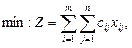
при ограничениях: 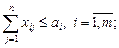
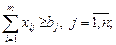
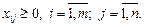
Если 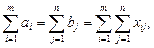 то задача называется закрытой (сбалансированной), в противном случае – открытой.
то задача называется закрытой (сбалансированной), в противном случае – открытой.
Переход к закрытой форме задачи. В случае, если запасы поставщиков больше потребностей потребителей 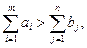 вводят (n + 1)-го фиктивного потребителя, запросы которого равны излишку запаса, т.е.
вводят (n + 1)-го фиктивного потребителя, запросы которого равны излишку запаса, т.е.
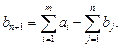
Тарифы 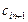 считаются равными нулю. Получим расширенную закрытую задачу. Поставки
считаются равными нулю. Получим расширенную закрытую задачу. Поставки  в оптимальном плане расширенной задачи покажут остатки продукции на складах поставщиков.
в оптимальном плане расширенной задачи покажут остатки продукции на складах поставщиков.
Если потребности превышают запасы  то вводят
то вводят 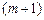 -го фиктивного поставщика. Его запасы считают равными недостающей продукции:
-го фиктивного поставщика. Его запасы считают равными недостающей продукции:
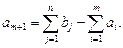
Тарифы  равны некоторому большому положительному числу. В расширенной задаче получим баланс потребностей и запасов. Поставки
равны некоторому большому положительному числу. В расширенной задаче получим баланс потребностей и запасов. Поставки  в оптимальном плане расширенной задачи покажут объемы недостачи продукции.
в оптимальном плане расширенной задачи покажут объемы недостачи продукции.
Транспортная задача может быть решена симплекс-методом. Благодаря специфике системы ограничений, разработаны методы поиска решения на матрице допустимых решений, что значительно упрощает процедуру симплексного метода. Специфика ограничений сбалансированной задачи:
· коэффициенты при 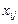 равны единице;
равны единице;
· каждая переменная 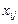 встречается дважды;
встречается дважды;
· в случае баланса всегда имеется допустимое решение задачи;
· число переменных в транспортной задаче равно nm, а число уравнений в системе ограничений равно 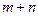 . Так как мы предполагаем, что транспортная задача является закрытой, то число линейно независимых уравнений равно
. Так как мы предполагаем, что транспортная задача является закрытой, то число линейно независимых уравнений равно 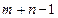 . Следовательно, опорный план транспортной задачи может иметь не более
. Следовательно, опорный план транспортной задачи может иметь не более 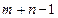 отличных от нуля неизвестных переменных.
отличных от нуля неизвестных переменных.
При любом методе решения транспортной задачи начинают с нахождения начального опорного плана.
Определение начального опорного плана задачи
Для определения опорного плана существуют несколько методов. Сущность этих методов состоит в том, что опорный план находят последовательно за 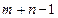 шагов, на каждом из которых в таблице условий задачи заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворение потребности в грузе одного из пунктов назначения (того, в столбце которого находится заполненная клетка), либо вывоз груза из одного из пунктов отправления (из того, в строке которого находится заполняемая клетка).
шагов, на каждом из которых в таблице условий задачи заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворение потребности в грузе одного из пунктов назначения (того, в столбце которого находится заполненная клетка), либо вывоз груза из одного из пунктов отправления (из того, в строке которого находится заполняемая клетка).
В первом случае временно исключают из рассмотрения столбец, содержащий заполненную на данном шаге клетку, и рассматривают задачу, таблица условий которой содержит на один столбец меньше, чем было перед этим шагом, но то же количество строк и соответственно измененные запасы груза в одном из пунктов отправления (в том, за счет запаса которого была удовлетворена потребность в грузе пункта назначения на данном шаге). Во втором случае временно исключают из рассмотрения строку, содержащую заполненную клетку, и считают, что таблица условий имеет на одну строку меньше при неизменном количестве столбцов и при соответствующем изменении потребности в грузе в пункте назначения, в столбце которого находится заполняемая клетка.
После того как проделаны 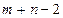 описанных выше шагов, получают задачу с одним пунктом отправления и одним пунктом назначения. При этом останется свободной только одна клетка, а запасы оставшегося пункта отправления будут равны потребностям оставшегося пункта назначения. Заполнив эту клетку, тем самым делают (
описанных выше шагов, получают задачу с одним пунктом отправления и одним пунктом назначения. При этом останется свободной только одна клетка, а запасы оставшегося пункта отправления будут равны потребностям оставшегося пункта назначения. Заполнив эту клетку, тем самым делают ( 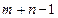 )- й шаг и получают искомый опорный план. Следует заметить, что на некотором шаге (но не на последнем) может оказаться, что потребности очередного пункта назначения равны запасам очередного пункта отправления. В этом случае также временно исключают из рассмотрения либо столбец, либо строку (что-нибудь одно). Таким образом, либо запасы соответствующего пункта отправления, либо потребности данного пункта назначения считают равными нулю. Этот нуль записывают в очередную заполняемую клетку. Указанные выше условия гарантируют получение
)- й шаг и получают искомый опорный план. Следует заметить, что на некотором шаге (но не на последнем) может оказаться, что потребности очередного пункта назначения равны запасам очередного пункта отправления. В этом случае также временно исключают из рассмотрения либо столбец, либо строку (что-нибудь одно). Таким образом, либо запасы соответствующего пункта отправления, либо потребности данного пункта назначения считают равными нулю. Этот нуль записывают в очередную заполняемую клетку. Указанные выше условия гарантируют получение 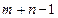 занятых клеток, в которых стоят компоненты опорного плана, что является исходным условием для проверки на оптимальность и нахождения оптимального плана.
занятых клеток, в которых стоят компоненты опорного плана, что является исходным условием для проверки на оптимальность и нахождения оптимального плана.
Метод северо-западного угла. При нахождении опорного плана транспортной задачи методом северо-западного угла на каждом шаге рассматривают первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначения. Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного х11 («северо-западный угол») и заканчивается клеткой для неизвестного хmn , т.е. идет как бы по диагонали таблицы.
Пример. На три базы А1, А2, А3 поступил однородный груз в количествах, соответственно равных 140, 180 и 160 ед. Этот груз требуется перевезти в пять пунктов назначения В1, В2, В3, В4, В5 соответственно в количествах 60, 70, 120, 130 и 100 ед. Тарифы перевозок единицы груза с каждого из пунктов отправления в соответствующие пункты назначения указаны в следующей таблице:
Таблица 8.1
| Пункты отправления | Пункты назначения | Запасы | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности |
Найти план перевозок данной транспортной задачи методом северо-западного угла.
Решение. Здесь число пунктов отправления  , а число пунктов назначения
, а число пунктов назначения 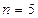 . Следовательно, опорный план задачи определяется числами, стоящими в 5+3-1=7 заполненных клетках.
. Следовательно, опорный план задачи определяется числами, стоящими в 5+3-1=7 заполненных клетках.
Заполнение таблицы начнем с клетки для неизвестного х11, т.е. попытаемся удовлетворить потребности первого пункта назначения за счет запасов первого пункта отправления. Так как запасы пункта А1 больше, чем потребности пункта В1, то полагаем 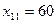 , записываем это значение в соответствующей клетке табл. 8.2 и временно исключаем из рассмотрения столбец В1, считая при этом запасы пункта А1 равными 80.
, записываем это значение в соответствующей клетке табл. 8.2 и временно исключаем из рассмотрения столбец В1, считая при этом запасы пункта А1 равными 80.
Таблица 8.2
| Пункты отправления | Пункты назначения | Запасы | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности |
Рассмотрим первые из оставшихся пунктов отправления А1 и назначения В2. Запасы пункта А1 больше потребностей пункта В2. Положим 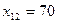 , запишем это значение в соответствующей клетке табл. 8.2 и временно исключим из рассмотрения столбец В2. В пункте А1 запасы считаем равными 10 ед. Снова рассмотрим первые из оставшихся пунктов отправления А1 и назначения В3. Потребности пункта В3 больше оставшихся запасов пункта А1. Положим
, запишем это значение в соответствующей клетке табл. 8.2 и временно исключим из рассмотрения столбец В2. В пункте А1 запасы считаем равными 10 ед. Снова рассмотрим первые из оставшихся пунктов отправления А1 и назначения В3. Потребности пункта В3 больше оставшихся запасов пункта А1. Положим 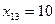 и запишем в соответствующую клетку табл. 8.2 и считаем потребности пункта В3 равными 110 ед.
и запишем в соответствующую клетку табл. 8.2 и считаем потребности пункта В3 равными 110 ед.
Теперь перейдем к заполнению клетки для неизвестного х23 и т.д. Через шесть шагов остается один пункт отправления А3 с запасом груза 100 ед. и один пункт назначения В5 с потребностью 100 ед. Соответственно имеется одна свободная клетка, которую и заполняем, полагая 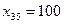 . В результате получаем опорный план
. В результате получаем опорный план
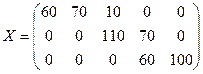 .
.
Согласно данному плану перевозок, общая стоимость перевозок всего груза составляет 
Метод минимального элемента. В методе северо-западного угла на каждом шаге потребности первого из оставшихся пунктов назначения удовлетворялись за счет запасов первого из оставшихся пунктов отправления. Очевидно, выбор пунктов отправления и назначения целесообразно производить, ориентируясь на тарифы перевозок, а именно: на каждом шаге следует выбирать какую-нибудь клетку, отвечающую минимальному тарифу (если таких клеток несколько, то следует выбрать любую из них), и рассмотреть пункты назначения и отправления, соответствующие выбранной клетке. Суть метода минимального элемента и состоит в выборе клетки с минимальным тарифом. Следует отметить, что этот метод, как правило, позволяет найти опорный план транспортной задачи, при котором общая стоимость перевозок груза меньше, чем общая стоимость перевозок при плане, найденном для данной задачи с помощью метода северо-западного угла (проверьте на предыдущем примере самостоятельно!). Поэтому наиболее целесообразно опорный план транспортной задачи находить методом минимального элемента.
Контрольные вопросы:
1. Приведите пример транспортной задачи.
2. Укажите отличия открытой транспортной задачи от закрытой.
3. Опишите метод северо-западного угла.
4. Опишите метод минимального элемента.
Лекция 9. Транспортная задача. Нахождение оптимального плана
План:
1. Метод потенциалов
Метод потенциалов
Для определения оптимального плана транспортной задачи разработано несколько методов. Однако наиболее часто используются метод потенциалов и метод дифференциальных рент.
Метод потенциалов. Общий принцип определения оптимального плана транспортной задачи методом потенциалов аналогичен принципу решения задачи линейного программирования симплексным методом, а именно: сначала находят опорный план транспортной задачи, а затем его последовательно улучшают до получения оптимального плана.
Для определения опорного плана транспортной задачи будем пользоваться одним из методов, рассмотренных выше. Эти методы гарантируют получение занятых в исходном плане  клеток, причем в некоторых из них могут стоять нули. Полученный план следует проверить на оптимальность.
клеток, причем в некоторых из них могут стоять нули. Полученный план следует проверить на оптимальность.
Теорема. Если для некоторого опорного плана 
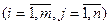 транспортной задачи существуют такие числа
транспортной задачи существуют такие числа 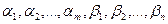 , что
, что
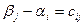 при
при 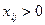 (8.1)
(8.1)
и
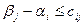 при
при 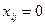 (8.2)
(8.2)
для всех 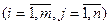 , то
, то  - оптимальный план транспортной задачи.
- оптимальный план транспортной задачи.
Определение. Числа 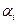 и
и 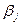
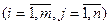 называются потенциалами соответственно пунктов назначения и пунктов отправления.
называются потенциалами соответственно пунктов назначения и пунктов отправления.
Сформулированная теорема позволяет построить алгоритм нахождения решения транспортной задачи. Он состоит в следующем. Пусть одним из рассмотренных выше методов найден опорный план транспортной задачи. Для каждого из пунктов отправления и назначения определяют потенциалы 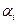 и
и 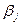
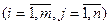 . Эти числа находят из системы уравнений
. Эти числа находят из системы уравнений
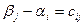 , (8.3)
, (8.3)
где 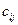 - тарифы, стоящие в заполненных клетках таблицы условий транспортной задачи.
- тарифы, стоящие в заполненных клетках таблицы условий транспортной задачи.
Так как число заполненных клеток равно 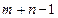 , то система (8.3) с
, то система (8.3) с 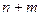 неизвестными содержит
неизвестными содержит 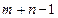 уравнений. Поскольку число неизвестных превышает на единицу число уравнений, одно из неизвестных можно положить равным произвольному числу, например
уравнений. Поскольку число неизвестных превышает на единицу число уравнений, одно из неизвестных можно положить равным произвольному числу, например 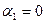 , и найти последовательно из уравнений (8.3) значения остальных неизвестных. После того как все потенциалы найдены, для каждой из свободных клеток определяют числа
, и найти последовательно из уравнений (8.3) значения остальных неизвестных. После того как все потенциалы найдены, для каждой из свободных клеток определяют числа 
 |
Если среди чисел  нет положительных, то найденный опорный план является оптимальным. Если же для некоторой свободной клетки
нет положительных, то найденный опорный план является оптимальным. Если же для некоторой свободной клетки 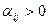 , то исходный опорный план не является оптимальным и необходимо перейти к новому опорному плану. Для этого рассматривают все свободные клетки, для которых
, то исходный опорный план не является оптимальным и необходимо перейти к новому опорному плану. Для этого рассматривают все свободные клетки, для которых 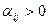 , и среди данных чисел выбирают максимальное. Клетку, которой это число соответствует, следует заполнить.
, и среди данных чисел выбирают максимальное. Клетку, которой это число соответствует, следует заполнить.
Заполняя выбранную клетку, необходимо изменить объемы поставок, записанных в ряде других занятых клеток и связанных с заполненной так называемым циклом.
Определение. Циклом в таблице условий транспортной задачи называется ломаная линия, вершины которой расположены в занятых клетках таблицы, а звенья – вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно из которых находится в строке, а другое – в столбце.
Если ломаная линия, образующая цикл, пересекается, то точки самопересечения не являются вершинами. Примеры некоторых циклов показаны на рис. 1.
При правильном построении опорного плана для любой свободной клетки можно построить лишь один цикл. После того как для выбранной свободной клетки он построен, следует перейти к новому опорному плану. Для этого необходимо переместить грузы в пределах клеток, связанных с данной свободной клеткой. Это перемещение производят по следующим правилам:
1) каждой из клеток, связанных циклом с данной свободной клеткой, приписывают определенный знак, причем свободной клетке – знак плюс, а всем остальным клеткам – поочередно знаки минус и плюс (будем называть эти клетки минусовыми и плюсовыми);
2) в данную свободную клетку переносят меньшее из чисел  , стоящих в минусовых клетках. Одновременно это число прибавляют к соответствующим числам, стоящим в плюсовых клетках, и вычитают из чисел, стоящих в минусовых клетках. Клетка, которая ранее была свободной, становится занятой, а минусовая клетка, в которой стояло минимальное из чисел
, стоящих в минусовых клетках. Одновременно это число прибавляют к соответствующим числам, стоящим в плюсовых клетках, и вычитают из чисел, стоящих в минусовых клетках. Клетка, которая ранее была свободной, становится занятой, а минусовая клетка, в которой стояло минимальное из чисел  , считается свободной.
, считается свободной.
В результате указанных выше перемещений грузов в пределах клеток, связанных циклом с данной свободной клеткой, определяют новый опорный план транспортной задачи.
Описанный выше переход от одного опорного плана транспортной задачи к другому ее опорному плану называется сдвигом по циклу пересчета.
Следует отметить, что при сдвиге по циклу пересчета число занятых клеток остается неизменным, а именно остается равным 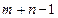 . При этом если в минусовых клетках имеется два (или более) одинаковых числа
. При этом если в минусовых клетках имеется два (или более) одинаковых числа  , то освобождают лишь одну из таких клеток, а остальные оставляют занятыми (с нулевыми поставками).
, то освобождают лишь одну из таких клеток, а остальные оставляют занятыми (с нулевыми поставками).
Полученный новый опорный план проверяют на оптимальность. Для этого определяют потенциалы пунктов отправления и назначения и находят числа 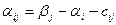 для всех свободных клеток. Если среди этих чисел не окажется положительных, то это свидетельствует о получении оптимального плана. Если же положительные числа имеются, то следует перейти к новому опорному плану. В результате итерационного процесса после конечного числа шагов получают оптимальный план задачи.
для всех свободных клеток. Если среди этих чисел не окажется положительных, то это свидетельствует о получении оптимального плана. Если же положительные числа имеются, то следует перейти к новому опорному плану. В результате итерационного процесса после конечного числа шагов получают оптимальный план задачи.
Из изложенного выше следует, что процесс нахождения решения транспортной задачи методом потенциалов включает следующие этапы:
1. Находят опорный план. При этом число заполненных клеток должно быть равным 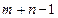 .
.
2. Находят потенциалы 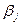 и
и 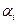 соответственно пунктов назначения и пунктов отправления.
соответственно пунктов назначения и пунктов отправления.
3. Для каждой свободной клетки определяют число  . Если среди чисел
. Если среди чисел  нет положительных, то получен оптимальный план транспортной задачи; если же они имеются, то переходят к новому опорному плану.
нет положительных, то получен оптимальный план транспортной задачи; если же они имеются, то переходят к новому опорному плану.
4. Среди положительных чисел  выбирают максимальное, строят для свободной клетки, которой оно соответствует, цикл пересчета и производят сдвиг по циклу пересчета.
выбирают максимальное, строят для свободной клетки, которой оно соответствует, цикл пересчета и производят сдвиг по циклу пересчета.
5. Полученный опорный план проверяют на оптимальность, т.е. снова повторяют все действия начиная с этапа 2.
В заключение отметим, что при определении опорного плана или в процессе решения задачи может быть получен вырожденный опорный план. Чтобы избежать в этом случае зацикливания, следует соответствующие нулевые элементы опорного плана заменить сколь угодно малым положительным числом 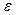 и решать задачу как невырожденную. В оптимальном плане такой задачи необходимо считать
и решать задачу как невырожденную. В оптимальном плане такой задачи необходимо считать 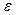 равным нулю.
равным нулю.
Пример. Для транспортной задачи, исходные данные которой приведены в табл. 8.3, найти оптимальный план.
Таблица 8.3
| Пункты отправления | Пункты назначения | Запасы | |||
| В1 | В2 | В3 | В4 | ||
| А1 | |||||
| А2 | |||||
| А3 | |||||
| Потребности |
Решение. Сначала, используя метод северо-западного угла, находим опорный план задачи. Этот план записан в табл. 8.3.
Найденный опорный план проверяем на оптимальность. В связи с этим находим потенциалы пунктов отправления и назначения. Для определения потенциалов получаем систему
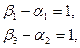
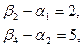

содержащую шесть уравнений с семью неизвестными. Полагая 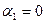 , находим
, находим 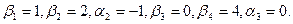 Для каждой свободной клетки вычисляем число
Для каждой свободной клетки вычисляем число 

Так как среди чисел  имеются положительные, то построенный план перевозок не является оптимальным и надо перейти к новому опорному плану. Наибольшим среди положительных чисел
имеются положительные, то построенный план перевозок не является оптимальным и надо перейти к новому опорному плану. Наибольшим среди положительных чисел  является
является 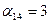 , поэтому для данной свободной клетки строим цикл пересчета (табл. 8.4) и производим сдвиг по этому циклу. Наименьшее из чисел в минусовых клетках равно 10. Клетка, в которой находится это число, становится свободной в новой табл. 8.5. Другие числа в табл. 8.5 получаются так: к числу 10, стоящему в плюсовой клетке табл. 8.4, добавим 10 и вычтем 10 из числа 20, находящегося в минусовой клетке табл. 8.4. Клетка на пересечении строки А2 и столбца В4 становится свободной.
, поэтому для данной свободной клетки строим цикл пересчета (табл. 8.4) и производим сдвиг по этому циклу. Наименьшее из чисел в минусовых клетках равно 10. Клетка, в которой находится это число, становится свободной в новой табл. 8.5. Другие числа в табл. 8.5 получаются так: к числу 10, стоящему в плюсовой клетке табл. 8.4, добавим 10 и вычтем 10 из числа 20, находящегося в минусовой клетке табл. 8.4. Клетка на пересечении строки А2 и столбца В4 становится свободной.
Таблица 8.4
| Пункты отправления | Пункты назначения | Запасы | |||
| В1 | В2 | В3 | В4 | ||
| А1 |
 - 20 - 20
| 1 + | |||
| А2 | + 10 | 5 - | |||
| А3 | |||||
| Потребности |
После этих преобразований получаем новый опорный план (табл. 8.5).
Таблица 8.5
| Пункты отправления | Пункты назначения | Запасы | |||
| В1 | В2 | В3 | В4 | ||
| А1 |
 - 10 - 10
| 1 + | |||
| А2 | |||||
| А3 | + | 4 - | |||
| Потребности |
Этот план проверяем на оптимальность. Снова находим потенциалы пунктов отправления и назначения. Для этого составляем следующую систему уравнений:

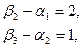

Полагаем 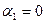 , получаем
, получаем 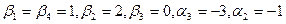 . Для каждой свободной клетки вычисляем числа
. Для каждой свободной клетки вычисляем числа  ; имеем,
; имеем, 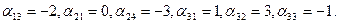
Таким образом, видим, что данный план перевозок не является оптимальным. Поэтому переходим к новому опорному плану (табл. 8.6).
Таблица 8.6
| Пункты отправления | Пункты назначения | Запасы | |||
| В1 | В2 | В3 | В4 | ||
| А1 | |||||
| А2 | |||||
| А3 | |||||
| Потребности |
Сравнивая разности 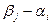 новых потенциалов, отвечающих свободным клеткам табл. 8.6, с соответствующими числами
новых потенциалов, отвечающих свободным клеткам табл. 8.6, с соответствующими числами 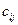 , видим, что указанные разности потенциалов для всех свободных клеток не превосходят соответствующих чисел
, видим, что указанные разности потенциалов для всех свободных клеток не превосходят соответствующих чисел 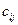 . Следовательно, полученный план
. Следовательно, полученный план
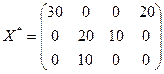
является оптимальным. При данном плане стоимость перевозок
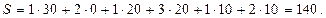
Контрольные вопросы:
1. Сформулируйте условие оптимальности.
2. Что такое контур, цена цикла?
3. Опишите метод потенциалов.
Дата добавления: 2015-11-06; просмотров: 1811;
