Практическое занятие №8
Нахождение опорного плана решения транспортной задачи
Цель: приобретение навыков нахождения опорного плана решения транспортной задачи.
Теоретические сведения: Пусть имеется 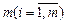 поставщиков (или пунктов отправления), располагающих некоторым однородным продуктом в объемах по
поставщиков (или пунктов отправления), располагающих некоторым однородным продуктом в объемах по 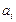 единиц, и
единиц, и 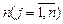 получателей (или пунктов назначения) с объемами потребления по
получателей (или пунктов назначения) с объемами потребления по 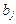 единиц. Задана матрица
единиц. Задана матрица 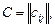 где
где  – стоимость перевозки единицы продукции от i-го поставщика j-му потребителю. Возникает задача определения плана перевозок
– стоимость перевозки единицы продукции от i-го поставщика j-му потребителю. Возникает задача определения плана перевозок 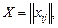 где
где 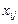 – количество единиц продукции, поставляемой по коммуникации (i, j), которая бы минимизировала суммарную стоимость всех перевозок. Математическая модель задачи будет иметь вид:
– количество единиц продукции, поставляемой по коммуникации (i, j), которая бы минимизировала суммарную стоимость всех перевозок. Математическая модель задачи будет иметь вид:
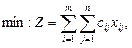
при ограничениях: 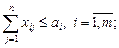
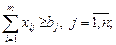
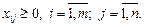
Если 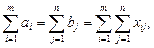 то задача называется закрытой (сбалансированной), в противном случае – открытой.
то задача называется закрытой (сбалансированной), в противном случае – открытой.
При любом методе решения транспортной задачи начинают с нахождения начального опорного плана.
Для определения опорного плана существуют несколько методов. Сущность этих методов состоит в том, что опорный план находят последовательно за 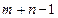 шагов, на каждом из которых в таблице условий задачи заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворение потребности в грузе одного из пунктов назначения (того, в столбце которого находится заполненная клетка), либо вывоз груза из одного из пунктов отправления (из того, в строке которого находится заполняемая клетка).
шагов, на каждом из которых в таблице условий задачи заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворение потребности в грузе одного из пунктов назначения (того, в столбце которого находится заполненная клетка), либо вывоз груза из одного из пунктов отправления (из того, в строке которого находится заполняемая клетка).
В первом случае временно исключают из рассмотрения столбец, содержащий заполненную на данном шаге клетку, и рассматривают задачу, таблица условий которой содержит на один столбец меньше, чем было перед этим шагом, но то же количество строк и соответственно измененные запасы груза в одном из пунктов отправления (в том, за счет запаса которого была удовлетворена потребность в грузе пункта назначения на данном шаге). Во втором случае временно исключают из рассмотрения строку, содержащую заполненную клетку, и считают, что таблица условий имеет на одну строку меньше при неизменном количестве столбцов и при соответствующем изменении потребности в грузе в пункте назначения, в столбце которого находится заполняемая клетка.
После того как проделаны 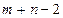 описанных выше шагов, получают задачу с одним пунктом отправления и одним пунктом назначения. При этом останется свободной только одна клетка, а запасы оставшегося пункта отправления будут равны потребностям оставшегося пункта назначения. Заполнив эту клетку, тем самым делают (
описанных выше шагов, получают задачу с одним пунктом отправления и одним пунктом назначения. При этом останется свободной только одна клетка, а запасы оставшегося пункта отправления будут равны потребностям оставшегося пункта назначения. Заполнив эту клетку, тем самым делают ( 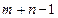 )- й шаг и получают искомый опорный план. Следует заметить, что на некотором шаге (но не на последнем) может оказаться, что потребности очередного пункта назначения равны запасам очередного пункта отправления. В этом случае также временно исключают из рассмотрения либо столбец, либо строку (что-нибудь одно). Таким образом, либо запасы соответствующего пункта отправления, либо потребности данного пункта назначения считают равными нулю. Этот нуль записывают в очередную заполняемую клетку. Указанные выше условия гарантируют получение
)- й шаг и получают искомый опорный план. Следует заметить, что на некотором шаге (но не на последнем) может оказаться, что потребности очередного пункта назначения равны запасам очередного пункта отправления. В этом случае также временно исключают из рассмотрения либо столбец, либо строку (что-нибудь одно). Таким образом, либо запасы соответствующего пункта отправления, либо потребности данного пункта назначения считают равными нулю. Этот нуль записывают в очередную заполняемую клетку. Указанные выше условия гарантируют получение 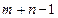 занятых клеток, в которых стоят компоненты опорного плана, что является исходным условием для проверки на оптимальность и нахождения оптимального плана.
занятых клеток, в которых стоят компоненты опорного плана, что является исходным условием для проверки на оптимальность и нахождения оптимального плана.
Метод северо-западного угла. При нахождении опорного плана транспортной задачи методом северо-западного угла на каждом шаге рассматривают первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначения. Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного х11 («северо-западный угол») и заканчивается клеткой для неизвестного хmn , т.е. идет как бы по диагонали таблицы.
Пример. На три базы А1, А2, А3 поступил однородный груз в количествах, соответственно равных 140, 180 и 160 ед. Этот груз требуется перевезти в пять пунктов назначения В1, В2, В3, В4, В5 соответственно в количествах 60, 70, 120, 130 и 100 ед. Тарифы перевозок единицы груза с каждого из пунктов отправления в соответствующие пункты назначения указаны в следующей таблице:
Таблица 8.1
| Пункты отправления | Пункты назначения | Запасы | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности |
Найти план перевозок данной транспортной задачи методом северо-западного угла.
Решение. Здесь число пунктов отправления  , а число пунктов назначения
, а число пунктов назначения 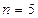 . Следовательно, опорный план задачи определяется числами, стоящими в 5+3-1=7 заполненных клетках.
. Следовательно, опорный план задачи определяется числами, стоящими в 5+3-1=7 заполненных клетках.
Заполнение таблицы начнем с клетки для неизвестного х11, т.е. попытаемся удовлетворить потребности первого пункта назначения за счет запасов первого пункта отправления. Так как запасы пункта А1 больше, чем потребности пункта В1, то полагаем 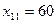 , записываем это значение в соответствующей клетке табл. 8.2 и временно исключаем из рассмотрения столбец В1, считая при этом запасы пункта А1 равными 80.
, записываем это значение в соответствующей клетке табл. 8.2 и временно исключаем из рассмотрения столбец В1, считая при этом запасы пункта А1 равными 80.
Таблица 8.2
| Пункты отправления | Пункты назначения | Запасы | ||||
| В1 | В2 | В3 | В4 | В5 | ||
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности |
Рассмотрим первые из оставшихся пунктов отправления А1 и назначения В2. Запасы пункта А1 больше потребностей пункта В2. Положим 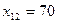 , запишем это значение в соответствующей клетке табл. 8.2 и временно исключим из рассмотрения столбец В2. В пункте А1 запасы считаем равными 10 ед. Снова рассмотрим первые из оставшихся пунктов отправления А1 и назначения В3. Потребности пункта В3 больше оставшихся запасов пункта А1. Положим
, запишем это значение в соответствующей клетке табл. 8.2 и временно исключим из рассмотрения столбец В2. В пункте А1 запасы считаем равными 10 ед. Снова рассмотрим первые из оставшихся пунктов отправления А1 и назначения В3. Потребности пункта В3 больше оставшихся запасов пункта А1. Положим 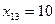 и запишем в соответствующую клетку табл. 8.2 и считаем потребности пункта В3 равными 110 ед.
и запишем в соответствующую клетку табл. 8.2 и считаем потребности пункта В3 равными 110 ед.
Теперь перейдем к заполнению клетки для неизвестного х23 и т.д. Через шесть шагов остается один пункт отправления А3 с запасом груза 100 ед. и один пункт назначения В5 с потребностью 100 ед. Соответственно имеется одна свободная клетка, которую и заполняем, полагая 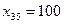 . В результате получаем опорный план
. В результате получаем опорный план
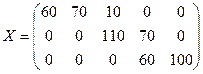 .
.
Согласно данному плану перевозок, общая стоимость перевозок всего груза составляет 
Метод минимального элемента. В методе северо-западного угла на каждом шаге потребности первого из оставшихся пунктов назначения удовлетворялись за счет запасов первого из оставшихся пунктов отправления. Очевидно, выбор пунктов отправления и назначения целесообразно производить, ориентируясь на тарифы перевозок, а именно: на каждом шаге следует выбирать какую-нибудь клетку, отвечающую минимальному тарифу (если таких клеток несколько, то следует выбрать любую из них), и рассмотреть пункты назначения и отправления, соответствующие выбранной клетке. Суть метода минимального элемента и состоит в выборе клетки с минимальным тарифом. Следует отметить, что этот метод, как правило, позволяет найти опорный план транспортной задачи, при котором общая стоимость перевозок груза меньше, чем общая стоимость перевозок при плане, найденном для данной задачи с помощью метода северо-западного угла (проверьте на предыдущем примере самостоятельно!). Поэтому наиболее целесообразно опорный план транспортной задачи находить методом минимального элемента.
Задание: для двух транспортных задач своего варианта найти опорный план двумя описанными выше способами.
Варианты:
1)
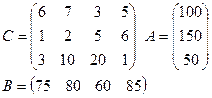
| 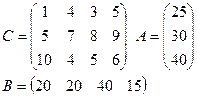
| ||
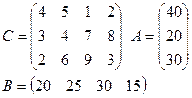
| 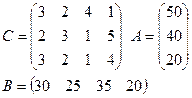
| ||
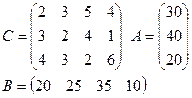
| 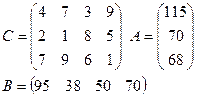
| ||
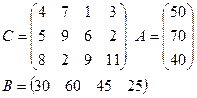
| 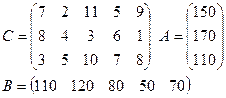
| ||
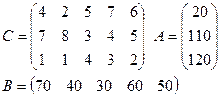
| 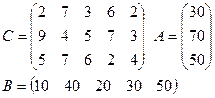
|
2)
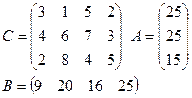
| 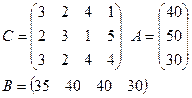
| ||
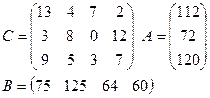
| 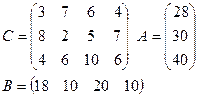
| ||
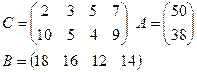
| 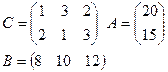
| ||
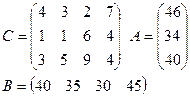
| 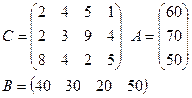
| ||
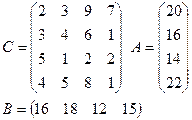
| 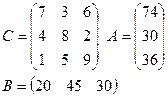
|
Контрольные вопросы:
1) В чем заключается экономический смысл транспортной задачи.
2) Запишите математическую модель транспортной задачи.
3) В чем суть метода северо-западного угла.
4) В чем суть метода минимального элемента.
Какой из методов наиболее предпочтителен для Вас. Обоснуйте
Дата добавления: 2015-11-06; просмотров: 1118;
