Поняття «відношення подільності» та його властивості.

1.Розглядаючи теоретико-множинну теорію цілих невід’ємних чисел, ми ввели означення відношення “ділитися націло”, розглянули його властивості. Як відомо, поділити ціле невід’ємне число а на натуральне число b це означає знайти таке ціле невід’ємне число с, що виконується рівність а=сb.

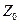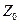Означення: якщо для ає і bÎ існує таке сÎ 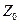, що виконується рівність а=сb, то говорять, що числа а і b знаходяться у відношенні подільності.

Означення: натуральне число а ділиться націло на натуральне число b, якщо існує додатній цілий корінь рівняння b×х=а.

Означення: натуральне число а не ділиться націло на натуральне число b, якщо не існує натурального кореня рівняння b×х=а.

Для позначення відношення подільності використовується такий символічний запис a 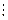b, який можна читати так: числа а і b знаходяться у відношення подільності, або а кратне b, або а ділиться націло на b, або b є дільником числа а. Відношення “ділитися націло” на множині цілих невід’ємних чисел є відношенням нестрогого порядку, бо володіє властивостями рефлексивності, антисиметричності та транзитивності. На основі цього відношення доводиться ряд теорем.