Схема № 1. Співвідношення між числовими множинами.

Різні підходи до побудови теорії цілих невід’ємних чисел.

2. Історія розвитку людства дає підстави для висновку про те, що розвиток математики спричинявся принаймні двома обставинами: по-перше, практичними потребами людини та, по-друге, потребами власне математики. Відповідно до цих потреб в математиці існують різні підходи до побудови теорії числових систем. Із шкільного курсу математики відомо, що існують натуральні, цілі, раціональні та дійсні числа (співвідношення між цими числовими множинами представлено за допомогою кругів Л.Ейлера на схемі №1). У курсі математики І-ІУ класів мають справу із невід’ємними цілими числами, до яких відносять об’єднання множини натуральних чисел (N={1, 2, 3, …, n, …}) і нуля. Цю множину прийнято позначати N₀ або Z₀. Розглянемо різні підходи до побудови теорії цілих невід’ємних чисел.

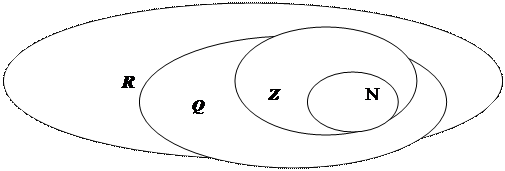Схема № 1. Співвідношення між числовими множинами.

У процесі практичної діяльності людині доводилося досить часто виконувати операції визначення кількості елементів скінченної множини, визначати порядок розміщення елементів множини, порівнювати множини за кількістю елементів у них, вимірювати певні величини. Для однозначного виконання, трактування та розуміння цих операцій необхідно було мати відповідні засоби. Створення таких засобів детермінувало появу різних трактувань поняття числа. Історично першими з’явилися натуральні числа, бо людині, в першу чергу, доводилося встановлювати чисельність елементів скінченної множини, потім – задавати порядок розміщення елементів у таких множинах, і, нарешті, - вимірювати величини. Таким чином, джерелами появи натуральних чисел можна вважати:

- необхідність встановлювати чисельність елементів скінченної множини, тобто потреби операції лічби;

- операцію вимірювання величин, тобто потреби у виконанні вимірювання різноманітних величин;

- необхідність задавати порядок розміщення елементів у скінченій множині, тобто операцію встановлення порядку розміщення елементів у множині.

Відповідно до вказаних операцій існують принаймні три теорії цілих невід’ємних чисел: 1) теоретико-множинна або кількісна; 2) аксіоматична або порядкова; 3) теорія цілих невід’ємних чисел, в якій число розглядається як результат вимірювання величини. Наявність різних теорій дозволяє більш детально задовольняти ті чи інші потреби практичної діяльності людини або науки математики. Кожна із вказаних теорій має свій рівень строгості з точки зору математики, свої позитивні та негативні риси. Не зупиняючись ґрунтовно на цих питаннях, бо вони не є предметом нашого розгляду і детально проаналізовані в теорії числових систем, розглянемо сутність побудови множини цілих невід’ємних чисел, використавши за основу операцію встановлення чисельності скінченної множини.