Внесок факторів виробництва в економічне зростання

Відповідно до методу обліку економічного зростання зв’язок між приростом продукту і джерелами цього приросту визначається за допомогою виробничої функції. При її використанні спочатку розглянемо лише джерела екстенсивного зростання і тому будемо спиратися на просту виробничу функцію:

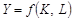. (10.12)

Отже, згідно з рівнянням (10.12) обсяг продукту може зростати прямо пропорційно факторам виробництва. Тобто коли обсяг факторів виробництва збільшується на 1 %, обсяг продукту також збільшується на 1 %. Але щоб розкрити апарат виробничої функції, слід нагадати, що результати трансформації факторів виробництва у продукт залежать від їх продуктивності: граничної продуктивності капіталу (МРK) і граничної продуктив­ності праці (MPL). Граничний продукт капіталу показує, на скільки збільшиться обсяг продукту, якщо обсяг капіталу зросте на одиницю за незмінної кількості інших факторів виробництва: MPK = DY / DK. Аналогічно, гранична продуктивність праці показує на скільки збільшиться обсяг продукту, якщо обсяг праці зросте на одиницю за незмінної кількості інших виробничих факторів: MPL = DY / DL.

Для спрощення аналізу будемо виходити з припущення про постійну віддачу від масштабу (постійний ефект від масштабу), яка означає, що зі збільшенням обсягів факторів виробництва їхня гранична продуктивність не змінюється. Спираючись на це припущення, визначимо вплив окремих факторів виробництва на приріст продукту. Так, якщо капітал збільшиться на DK одиниць, то приріст продукту становитиме MPK × DK одиниць. Аналогічно, у разі збільшення обсягів праці на DL одиниць обсяг продукту зросте на MPL × DL одиниць. Звідси вплив обох факторів виробництва на зростання продукту визначиться за формулою

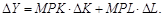(10.13)

Рівняння (10.13) визначає абсолютний приріст продукту. Щоб обчислити темп приросту продукту, який відображує темп економічного зростання, поділимо всі елементи цього рівняння на Y:

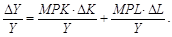(10.14)

Після цього помножимо перший член правої частини рівняння на вираз K / K, а другий — на вираз L / L, що не може змінити їх величину. Внаслідок певної трансформації цього рівняння отримаємо:

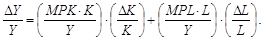(10.15)

Тепер розкриємо зміст окремих складових рівняння (10.15). Ліва частина цього рівняння DY / Y — це темп приросту продукту. В правій його частині член MPK × K відображує продукт, що створюється капіталом, а член (MPK × K) / Y є часткою капіталу у виробленому продукті. Аналогічно, член MPK × L є продуктом, який створюється працею, а член (MPL × K) / Y є часткою праці у виробленому продукті.

Врахуємо, що виробнича функція спирається на припущення про постійну віддачу від масштабу. За цих умов сума часток капіталу і праці у виробленому продукті дорівнює одиниці. Якщо частку капіталу у виробленому продукті позначити символом α, то частка праці дорівнюватиме (1 – α). Звідси випливає спрощена форма рівняння, яке пов’язує темп приросту продукту із темпом приросту капіталу і праці:

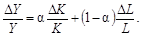(10.16)

Рівняння (10.16) дає змогу підвести підсумки щодо визначення внеску окремих факторів виробництва у приріст продукту. Згідно з цим рівнянням вираз α × DK / K відображує внесок капіталу в приріст продукту, а вираз (1 – α) × DL / L — внесок праці в його приріст.