Параметрический синтез

После синтеза структуры (если она не сопровождалась синтезом параметров) выполняется параметрический синтез. Вариант синтеза путем решения задачи оптимизации широко описан в литературе, поэтому рассмотрим генерационный параметрический синтез, т. е. расчет параметров по системе формул или уравнений без оптимизации, обеспечивающей получение работоспособного варианта объекта. Задача ставится таким образом. Пусть функционирование ВС обеспечивается при выполнении системы соотношений (формул) 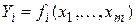i=1, m, 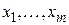- параметры ВС. Необходимо определить последовательность применения формул расчета при задании некоторой части параметров, т. е. необходимо синтезировать методику расчета по известным формулам.

Решение состоит в определении такой цепочки причинно-следственной связи в формулах (ранжирование формул), в которой расчет по первой формуле в этой цепочке позволил бы найти величины, необходимые для расчета, по второй формуле и т. д. По существу данная задача состоит в планировании вычислений. Алгоритмы и программы, решающие эту задачу, в теории ИИ получили название концептуальных решателей или планировщиков. Суть алгоритма планирования заключается в следующем. Найдем сначала формулу с минимальным числом неизвестных, например, с одной неизвестной, и вычислим ее. Далее снова найдем новую формулу с новой неизвестной и также вычислим ее и т. д. Легко заметить, что если построить матрицу, столбцы которой соответствуют неизвестным 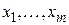(часть из них задана), а строки — номерам формул, то при отыскании искомой последовательности расчета эта матрица будет иметь строго трапециевидную структуру:

а) расчет только по формулам (рис. 3.7, а);

б) расчет с решением системы уравнений относительно X₇, X₆; На рисунке показан случай, когда X₁ рассчитывается по формуле на основе известных X₂, X₅, а для расчета X₇, X₆, нужно решить систему из двух уравнений, после чего X₄, .X₃ опять можно рассчитать по формулам (рис. 3.7, б).

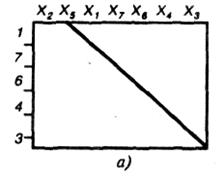
Рис. 3.7 – Построение матрицы по алгоритму планирования:
а – расчет только по формулам; б – расчет с решением системы уравнений относительно X₇, X₆; 1, 7, 6, 4, 3 – номера формул;
X₂, X₅ - заданные вершины; X₁, X₇, X₆, X₄, X₃ - искомые вершины

Для автоматизации планирования можно каждую формулу заменить фреймовой системой инструкций. Например, для формулы X₁=f₁(X₂, X₅) можно записать:

· если известно X₅, X₂, то известно X₁;

· если известно X₁, X₂, то известно X₅;

· если известно X₅, X₁, то известно X₂;

· если известно X₅, X₂, X₁, то неизвестных нет;

· если известно X₁, то неизвестно X₂, X₅ и т. д.

Представляя каждую формулу в указанном виде (этот процесс легко автоматизировать, записывая и вводя в программу через дисплей лишь исходную формулу) и последовательно многократно просматривая их, можно определять порядок активизации каждой формулы, т. е. последовательность их использования в синтезируемой методике расчета. Но данный формализм правил соответствует формированию семантической вычислительной сети. Однако возможны и другие алгоритмы прямого определения структуры матриц, не связанные с построением семантических сетей (рис. 3.8).

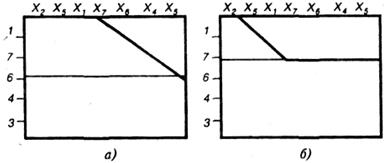
Рис. 3.8 – Алгоритм прямого определения структуры матрицы:
а – случай переопределения (число формул больше неизвестных);
б – случай недоопределения; 1, 7, 6, 4, 3 – номера формул

Заключение

Технические средства, информационное обеспечение САПР позволяют создавать качественно новые вычислительные системы.

Усложнение функций проектирования потребовало разработки интеллектуальных САПР: моделирующих и синтезирующих. Организация САПР с элементами искусственного интеллекта позволяет по-новому подойти к проблеме создания вычислительных устройств с переменной структурой, использовать методы структурного и параметрического синтеза, применять количественные и качественные характеристики.

Часть 4