Примеры решения задач. 1. В широкой части горизонтальной трубы вода течет со скоростью
1. В широкой части горизонтальной трубы вода течет со скоростью 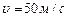 . Определить скорость течения воды в узкой части трубы, если разность давлений в широкой и узкой ее частях равна
. Определить скорость течения воды в узкой части трубы, если разность давлений в широкой и узкой ее частях равна 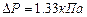
Решение:
Запишем уравнение Бернулли 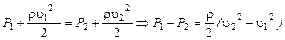
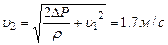
Формула Пуазейля
Наибольшей скоростью обладают частицы, движущиеся вдоль оси трубы; самый близкий к трубе слой жидкости неподвижен.
Для установления зависимости 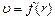 выделим мысленно цилиндрический объем жидкости радиуса r и длины l. На торцах этого цилиндра поддерживаются давления P1 и P2, что обуславливает результирующую силу.
выделим мысленно цилиндрический объем жидкости радиуса r и длины l. На торцах этого цилиндра поддерживаются давления P1 и P2, что обуславливает результирующую силу.


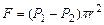 (1)
(1)
На боковую поверхность цилиндра со стороны окружающего слоя жидкости действует сила внутреннего трения, равная
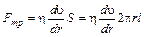 (2)
(2)
Где 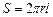 - площадь боковой поверхности цилиндра.
- площадь боковой поверхности цилиндра.
F=Fтр 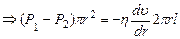 (3)
(3)
Знак (-), так как 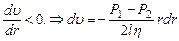 (4)
(4)
Проинтегрируем это уравнение:
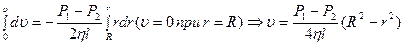 (5)
(5)
Наибольшую скорость имеет слой, текущий вдоль оси трубы (r=0): 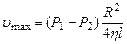
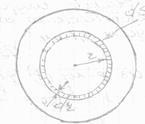
Определим объемную скорость кровотока Q. Для этого выделим цилиндрический слой радиусом r и толщиной dr. Площадь сечения этого слоя 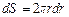 . За 1с слой переносит объем жидкости
. За 1с слой переносит объем жидкости 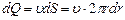 (6)
(6)
(5) 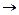 (6) получим
(6) получим 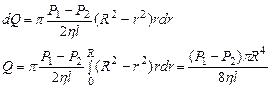 (7)
(7)
(7) - Формула Пуазейля
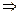 Через трубу протекает тем больше жидкости , чем меньше ее вязкость и больше радиус трубы.
Через трубу протекает тем больше жидкости , чем меньше ее вязкость и больше радиус трубы.
Формула Пуазейля аналогична закону Ома для участка цепи. Разность потенциалов соответствует разности давлений на концах трубы, сила тока - объемной скорости, электрическое сопротивление - гидравлическому сопротивлению
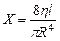 (8)
(8)
Гидравлическое сопротивление тем больше, чем больше вязкость 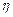 , длина l трубы и меньше сечение.
, длина l трубы и меньше сечение.
Дата добавления: 2015-10-29; просмотров: 1193;
