Средняя ошибка выборки
После завершения отбора необходимого числа единиц в выборку и регистрации предусмотренных программой наблюдения изучаемых признаков этих единиц, переходят к расчету обобщающих показателей. К ним относят среднюю величину изучаемого признака и долю единиц, обладающих каким-либо значением этого признака. Однако, если ГС произвести несколько выборок, определив при этом их обобщающие характеристики, то можно установить, что их значения будут различными, кроме того, они будут отличаться и от реального их значения в ГС, если такое определить с помощью сплошного наблюдения. Другими словами, обобщающие характеристики, рассчитанные по данным выборки, будут отличаться от их реальных значений в ГС, поэтому введем следующие условные обозначения (табл. 23).
Таблица 23. Условные обозначения
| Показатель | Совокупность | |
| генеральная | выборочная | |
| Число единиц совокупности | N | n |
| Среднее значение | 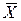
| 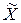
|
| Доля единиц, обладающих каким-либо значением признака | d | 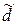
|
| Доля единиц, не обладающих каким-либо значением признака | 1-d | 1- 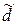
|
| Дисперсия | 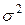
| 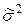
|
Разность между значением обобщающих характеристик выборочной и генеральной совокупностей называется ошибкой выборки, которая подразделяется на ошибку регистрации и ошибку репрезентативности. Первая возникает из-за неправильных или неточных сведений по причинам непонимания существа вопроса, невнимательности регистратора при заполнении анкет, формуляров и т.п. Она достаточно легко обнаруживается и устраняется. Вторая возникает из-за несоблюдения принципа случайности отбора единиц в выборку. Ее сложнее обнаружить и устранить, она гораздо больше первой и потому ее измерение является основной задачей выборочного наблюдения.
Для измерения ошибки выборки определяется ее средняя ошибка по формуле (65) для повторного отбора и по формуле (66) – для бесповторного:
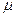 =
= 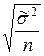 ;(65)
;(65) 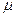 =
= 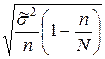 . (66)
. (66)
Из формул (65) и (66) видно, что средняя ошибка меньше у бесповторной выборки, что и обусловливает ее более широкое применение.
Дата добавления: 2015-10-26; просмотров: 904;
