СРЕДНЯЯ, СРЕДНЕКВАДРАТИЧНАЯ И НАИБОЛЕЕ ВЕРОЯТНАЯ СКОРОСТИ
В идеальном газе основную часть всего времени частицы, каждая из них, находятся сравнительно далеко друг от друга, и движутся свободно. Взаимодействия, как указывалось, происходит по законам абсолютно упругого столкновения, в процессе которого частицы обмениваются энергиями и импульсами.
 Будем рассматривать равновесное состояние. Рассмотрим процесс столкновения двух частиц. Пусть в некоторой точке пространства столкнулись две частицы с импульсами,
Будем рассматривать равновесное состояние. Рассмотрим процесс столкновения двух частиц. Пусть в некоторой точке пространства столкнулись две частицы с импульсами, 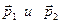 в результате взаимодействия они получат импульсы
в результате взаимодействия они получат импульсы 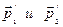 . Это прямой процесс. Обратным процессом называется процесс столкновения частиц с импульсами
. Это прямой процесс. Обратным процессом называется процесс столкновения частиц с импульсами 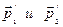 в результате которого они
в результате которого они
приобретают импульсы 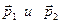 .в состоянии равновесия вероятность прямого и обратного процесса равны, т.к. в противном случае мы будем иметь направленное изменение импульсов. Если, скажем, будут преобладать прямые процессы, то будет увеличиваться число частиц с импульсами
.в состоянии равновесия вероятность прямого и обратного процесса равны, т.к. в противном случае мы будем иметь направленное изменение импульсов. Если, скажем, будут преобладать прямые процессы, то будет увеличиваться число частиц с импульсами 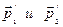 , что и приведет к упорядочению в системе, а это значит, система самопроизвольно выйдет из состояния равновесия, чего быть не может. Т.е. вероятности прямого и обратного процессов равны. Это утверждение называется принципом детального равновесия.
, что и приведет к упорядочению в системе, а это значит, система самопроизвольно выйдет из состояния равновесия, чего быть не может. Т.е. вероятности прямого и обратного процессов равны. Это утверждение называется принципом детального равновесия.
На основе этого принципа было получено распределение Максвелла.
Было введено пространство скоростей. Скорости имеют всевозможные направления, распределение скоростей изотропно. Выберем три произвольных взаимоперпендикулярных направления и на них спроектируем все скорости. Т.е. можно сказать, что скорости частиц образуют трехмерное пространство, которое будем называть пространством скоростей. Элемент объема в таком пространстве будет 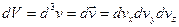 ,
, 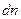 - среднее число частиц в этом объеме, т.е. число частиц, скорости которых лежат в интервале от
- среднее число частиц в этом объеме, т.е. число частиц, скорости которых лежат в интервале от 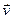 до
до 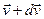 .
.
Пусть в реальном пространстве газ занимает единичный объем, тогда число частиц равно n. Вероятность того, что скорости частиц будут лежать в указанном интервале есть:
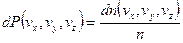
с другой стороны
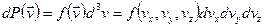
Сравнивая получим:
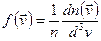
по смыслу это относительное число частиц, скорости которых лежат в единичном интервале скоростей вблизи заданного значения.
Были получены функции распределения:
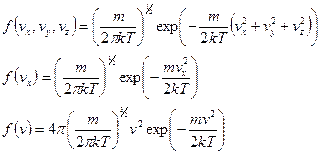
Построим графики функций. По смыслу 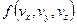 дает вероятность попадания частицы в определенное состояние в пространстве скоростей, которое характеризуется значениями компонент в единичном интервале вблизи
дает вероятность попадания частицы в определенное состояние в пространстве скоростей, которое характеризуется значениями компонент в единичном интервале вблизи 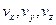 .
.
Первую функцию нельзя изобразить на графике, т.к. нельзя изобразить графически функцию трех переменных.
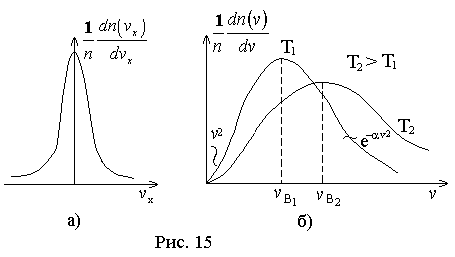 |
Изобразим графики функций двух оставшихся. Из графика
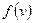 видно, что относительное число частиц с очень малыми и очень большими значениями сравнительно мало. Тем не менее всегда можно найти определенное число частиц молекул с очень малыми и очень большими скоростями. Функция
видно, что относительное число частиц с очень малыми и очень большими значениями сравнительно мало. Тем не менее всегда можно найти определенное число частиц молекул с очень малыми и очень большими скоростями. Функция 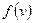 имеет максимум при значении скорости, которая называется наиболее вероятной. Эта функция несимметрична. Площадь под кривой левее
имеет максимум при значении скорости, которая называется наиболее вероятной. Эта функция несимметрична. Площадь под кривой левее 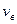 меньше, чем площадь справа. Максимум определяется конкуренцией
меньше, чем площадь справа. Максимум определяется конкуренцией 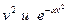 . С ростом температуры максимум функции понижается и смещается в сторону больших скоростей.
. С ростом температуры максимум функции понижается и смещается в сторону больших скоростей.
Зная распределение, можно найти наиболее вероятное значение скорости частиц и средние значения любых величин, характеризующих свойства газовых молекул.
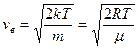
Средняя скорость
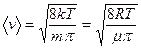
Средняя квадратичная скорость
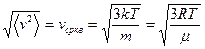
Из полученных результатов видно, что характерные скорости возрастают с ростом температуры. Скорости связаны соотношением
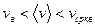 легко получить
легко получить 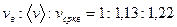
Аналогичным образом, используя соответствующие функции распределения, можно найти среднее значение энергии, импульса и других величин.
Решение задач.
Л Е К Ц И Я 2
Первое начало термодинамики. Внутренняя энергия. Закон о равнораспределении энергии по степеням свободы. Количество тепла. Работа, совершаемая газом. Теплоемкость. Уравнение Р. Майера.
Решение задач: 5.66, 5.68, 5.70, 5.88
Внутренняя энергия тела включает в себя кинетическую энергию хаотического движения молекул, потенциальную энергию взаимодействия между молекулами и внутримолекулярную энергию.
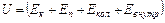
Здесь: 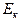 - кинетическая энергия хаотического движения молекул,
- кинетическая энергия хаотического движения молекул, 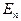 - потенциальная энергия взаимодействия молекул между собой,
- потенциальная энергия взаимодействия молекул между собой, 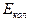 - энергия колебательного движения атомов в молекулах,
- энергия колебательного движения атомов в молекулах, 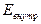 - энергия внутриатомного взаимодействия (изучается в атомной физике).
- энергия внутриатомного взаимодействия (изучается в атомной физике).
Внутренняя энергия системы тел равна сумме внутренних энергий каждого из тел в отдельности и энергии взаимодействия между телами.
Внутренняя энергия величина аддитивная. Она является функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, ее внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе системы из одного состояния в другое будет равна разности значений внутренней энергии в этих состояниях, независимо от пути, по которому совершался переход, т.е. независимо от процесса.
Для идеального газа 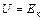 .
.
Для одной одноатомной молекулы 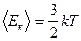 .
.
Для одного моля 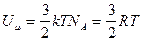 .
.
Для произвольной массы газа:
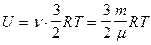 .
.
Таким образом внутренняя энергия идеального газа зависит только от температуры и не зависит от 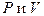 - закон Джоуля. В идеальном газе молекулы - материальные точки. Тогда
- закон Джоуля. В идеальном газе молекулы - материальные точки. Тогда
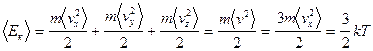 ,
,
т.е. 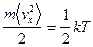 , с учетом того, что у материальной точки 3 степени свободы приходим к следующему выводу: на долю каждой степени свободы приходится одинаковая энергия.
, с учетом того, что у материальной точки 3 степени свободы приходим к следующему выводу: на долю каждой степени свободы приходится одинаковая энергия.
Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение системы.
На одну степень свободы идеального газа приходится одинаковая энергия, равная 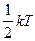 - теорема о равнораспределении энергии по степеням свободы. При хаотическом движении молекул все виды движения равноправны. Тогда для двухатомных жестких молекул
- теорема о равнораспределении энергии по степеням свободы. При хаотическом движении молекул все виды движения равноправны. Тогда для двухатомных жестких молекул
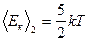 .
.
Для трехатомных жестких молекул
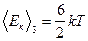 .
.
Если молекулы не являются жесткими, то необходимо учитывать колебательные степени свободы.
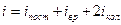
На колебательную степень свободы приходится вдвое большая энергия чем на поступательную или вращательную.
Поступательное и вращательное движение молекулы связано с наличием только кинетической энергии, а колебательное движение молекулы связано с наличием кинетической, и потенциальной энергии, причем для гармонического осциллятора среднее значение кинетической и потенциальной энергии оказывается одинаковым. Поэтому на каждую колебательную степень свободы должны приходиться в среднем две половинки 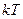 .
.
Молекулы идеального газа не взаимодействуют между собой. Поэтому внутренняя энергия одного моля идеального газа можно найти, умножив число Авагадро на среднюю энергию одной молекулы:
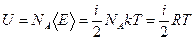
Внутренняя энергия может изменяться за счет совершения телом работы над внешними телами и сообщения ему количества теплоты.
Совокупность микроскопических процессов, приводящих к передаче энергии от тела к телу называют теплопередачей.
Количество энергии, переданное от тела к телу путем теплопередачи, называется количеством теплоты, отданного одним телом другому.
Запишем уравнение
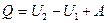
Это уравнение выражает закон сохранения энергии и носит название 1 начала термодинамики:
Количество теплоты, сообщенное системе, идет на приращение внутренней энергии и на совершение работы над внешними телами.
В дифференциальной форме 1 начало термодинамики имеет вид:
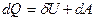
Q и А – являются функциями процесса. Они зависят от пути перехода системы из одного состояния в другое.
Рассказать первое начало термодинамики для всех изопроцессов.
Дата добавления: 2015-10-26; просмотров: 2707;
