РАБОТА, СОВЕРШАЕМАЯ ИДЕАЛЬНЫМ ГАЗОМ ПРИ РАЗЛИЧНЫХ ПРОЦЕССАХ

Работа, которая совершается при переходе из состояния 1 в состояние 2 каким-либо телом над внешними телами, равна

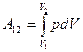
Уравнение политропы идеального газа можно записать

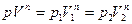
где 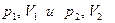- значения давления и объема газа соответственно в начальном и конечном состояниях, 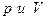- давления и объем в промежуточном состоянии. Выразим р:

Подставим в работу

После интегрирования получим:

Учитывая, что газ идеальный данное выражение можно записать иначе, используя уравнение состояния идеального газа:

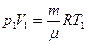
Тогда получим:

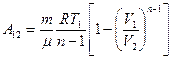
При адиабатическом процессе

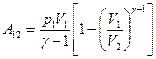
или

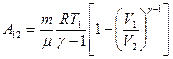
Вычислим работу идеального газа при изотермическом процессе, заменив давление через другие величины, согласно уравнению Менделеева-Клапейрона:

Работа, совершаемая при изобарическом процессе:

При изохорном процессе работа равна нулю.

Решение задач.

Л Е К Ц И Я 4

Второе начало термодинамики. Тепловые машины. К.П.Д. тепловых машин. Цикл Карно. Энтропия.

I начало ничего не говорит о направлении процессов, оно только требует чтобы при любом процессе выполнялся закон сохранения энергии. Например I начало не запрещает самопроизвольный переход тепла от тела менее нагретого к более нагретому. Между тем, направление процессов в термодинамике крайне важно.

II начало термодинамики устанавливает направление процессов, позволяет построить термодинамическую температурную шкалу, не зависящую от выбора температуры тела, позволяет установить ряд важных термодинамических состояний.

Тепловые процессы могут быть обратимыми и необратимыми. В этом их принципиальное отличие от механических явлений, в механике все обратимо.

Если в стакан воды капнуть чернил, они равномерно окрасят воду и назад в каплю никогда не соберутся.

Растворение солей, остывание тел, расширение газа в пустоту - примеры необратимых процессов. Если система переходит из состояния 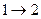и каким-либо способом ее можно вернуть назад , такой процесс обратим, если этого сделать нельзя -необратим. Теплопроводность - пример необратимого процесса.

Обратимы все равновесные процессы.

Если система перейдет в исходное состояние по тем же промежуточным состояниям, обратимость в узком смысле слова, если безразлично каким способом - обратимость в широком смысле слова. Все квазистатические процессы обратимы и притом в узком смысле слова.

Циклический процесс - процесс, в результате которого система возвращается в исходное состояние, описывая некоторую обратимую траекторию на фазовой плоскости.

Основоположником II начала термодинамики является французский инженер Сади Карно. Он одним из первых обратил внимание на неравноправность перехода .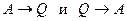

Второй закон устанавливает направление течения и характер процессов, происходящих в природе. Согласно Клаузиусу: теплота не может самопроизвольно переходить от менее нагретого тела к более нагретому. Это означает, что для такого перехода теплоты требуется затрата работы внешнего источника, что осуществляется в холодильной машине.

Физический смысл второго закона наиболее ясно раскрывается в формулировке Планка: Невозможен такой периодический процесс, единственным результатом которого было бы превращение теплоты в работу.

Всякий двигатель представляет собой систему, совершающую многократно некий круговой процесс (цикл). Пусть в ходе цикла рабочее вещество сначала расширяется до объема 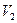, а затем снова сжимается до объема .Чтобы работа за цикл была больше нуля, давление в процессе расширения должно быть больше, чем при сжатии. Для этого рабочему телу нужно в ходе расширения сообщить тепло, а входе сжатия отнимать от него тепло. Совершив цикл, рабочее вещество возвращается в исходное состояние. Поэтому изменение внутренней энергии за цикл равно нулю. Количество тепла, сообщаемого рабочему телу за цикл равно , где 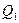- тепло, получаемое рабочим телом, а - тепло, отдаваемое при сжатии. Работа, совершаемая за цикл, равна площади цикла.

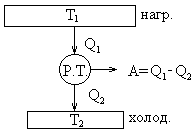
Периодически действующий двигатель, совершающий работу за счет получаемого извне тепла, называется тепловой машиной.

Тепловая машина состоит.6 нагреватель, холодильник и рабочее тело.

Тепловую машину принято характеризовать коэффициентом полезного действия, который определяется как отношение совершаемой за цикл работы А к получаемому за цикл теплу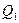

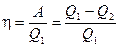
К.п.д. не может быть больше единицы.

Если обратить цикл, получится цикл холодильной машины.

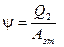
Обратимый цикл, совершаемый телом, состоит из двух изотерм и двух адиабат. Такой цикл называют циклом Карно.

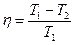к.п.д. цикл Карно.

Для холодильной машины Карно

.

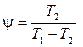Теоремы Карно

1. 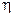- определяется только температурой холодильника и нагревателя и не зависит от рабочего вещества совершающего цикл (ее докажем позже).

2. Любая тепловая машина не может иметь 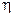больше чем машина Карно, работающая при тех же температурах нагревателя и холодильника.

Формулу коэффициента полезного действия идеальной тепловой машины, работающей по циклу Карно

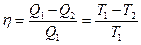
легко привести к виду

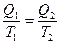
Отношение количества переданной теплоты к температуре теплоотдатчика или теплоприемника называется приведенной теплотой.

Энтропия.

Рассмотрим переход системы из состояния 1 в 2 по двум разным фазовым траекториям. Разобьем пути перехода на участки, на которых система получает 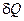при температуре .

.

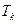Построим отношение 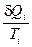, 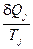и найдем сумму приведенных теплот по всему пути I+II: .

.

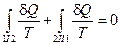
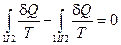
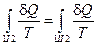Тогда равенство Клаузиуса можно сформулировать следующим образом:

Приведенное количество теплоты, полученное системой при любом квазистатическом круговом процессе, равно нулю.

Или: Приведенное количество тепла, квазистатически полученное системой не зависит от пути перехода, а определяется лишь начальным и конечным состоянием системы.

Этот важный результат позволяет вывести новую функцию состояния: энтропию.

Энтропия системы есть функция ее состояния, определенная с точностью до произвольной постоянной. Разность энтропий в двух равновесных состояниях 2 и 1, по определению равна приведенному количеству тепла, которое нужно сообщить системе, чтобы перевести ее из состояния 1 в состояние 2 по любому квазистатическому пути. Обозначают буквой S

Значение произвольной постоянной роли не играет, т.к. смысл имеет только разность энтропий. Условно, энтропию в каком либо состоянии можно принять за ноль, тогда определится и значение произвольной постоянной. Итак, по определению

.

Причем интеграл берется по любому квазистатическому пути, переводящему систему в данное состояние из другого, принятого за начальное. Дифференциал функции:

только для квазистатических процессов,

то есть если есть количество тепла, квазистатически полученное системой, то после деления на температуру оно переходит в полный дифференциал функции состояния энтропии.

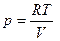для 1 моля

.

Тогда

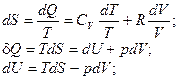
для квазистатических процессов.

.

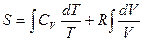Если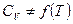

.

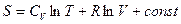Для 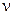молей

.

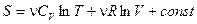Физические свойства энтропии.

Интуитивных представлений, облегчающих понимание смысла энтропии нет, это понятие связано с нашими повседневными представлениями. Чем, например, отличается S ведра с водой от энтропии окружающего воздуха.

1) При переходе из 1 в 2

.

Причем 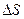не зависит от того, по какому квазистатическому пути осуществлен этот переход.

2)

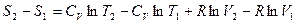
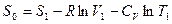
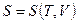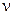Энтропия определена с точностью до аддитивной постоянной для молей

,

то есть сама энтропия величина аддитивная, ее значение пропорционально числу частиц в системе.

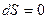3) При квазистатическом адиабатическом процессе , следовательно, S=const, таким образом, адиабатические процессы – изоэнтропийные.

Л Е К Ц И Я

Реальные газы. Понятие о межмолекулярных силах. Уравнение Ван-дер-Ваальса

Согласно закону Бойля-Мариотта, произведение объема газа на его давление для данной массы газа должно оставаться постоянным при любом давлении. Однако в действительности этот закон соблюдается удовлетворительно лишь при небольших давлениях и достаточно высоких температурах. При рассмотрении идеальных газов мы в ряде случаев, например при выводе основного уравнения кинетической теории газов, предполагали, что молекулы подобны материальным точкам, их объем не принимался во внимание. Почти во всех случаях не учитывались силы взаимодействия молекул на расстоянии. Наличие межмолекулярных сил и конечные размеры молекул являются основным отличием реальных газов от рассматривавшихся ранее идеальных.

Силы, действующие между молекулами, в основном являются электрическими силами. Силы отталкивания между молекулами изменяются с расстоянием значительно быстрее, чем силы притяжения.

Таким образом, взаимодействие сводится к рассмотрению сил электрического притяжения и отталкивания.

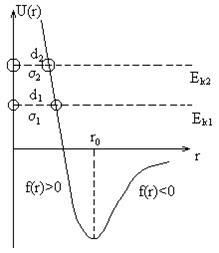Рассмотрим процесс столкновения двух частиц с учетом зависимости . При , при . Зная можно найти силы взаимодействия

.

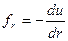При 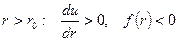- это по природе силы притяжения.

При - силы отталкивания.

При 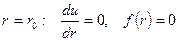- то есть силы притяжения и отталкивания компенсируются.

Пусть одна молекула не подвижна, а вторая движется к ней 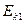. До ее скорость возрастает, потенциальная энергия убывает, после наоборот, т.к. начинают действовать силы отталкивания.

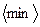расстояние, на которое могут сблизиться молекулы, называется 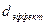. Таким образом, величина 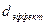зависит от скорости молекулы, чем больше 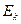, тем ближе будут расположены центры молекул при столкновении, тем меньше будет эффективный диаметр.

В случае идеального газа молекулы рассматривались как идеально твердые шары не взаимодействующие между собой. Потенциал для них представлен на рисунке. Кинетическая теория не зависела от расстояния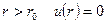. При , при 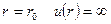, то есть имеется потенциальный барьер, через который частица проникнуть не может. В теории Ван-дер-Ваальса молекулы рассматриваются как твердые недеформируемые шары, между которыми существуют силы притяжения. Потенциал такого взаимодействия показан на рисунке. Причем расстояние играет роль диаметра молекулы. Влияние сил отталкивания сводится к наличию конечных размеров.

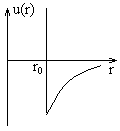
Уравнение молекулярно - кинетической теории 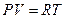хорошо описывает состояние реальных газов только при высоких T и сравнительно низких давлениях. Эксперимент показывает, что при T=const, 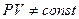с повышением давления. 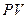сначала понижается, а затем растет, почти по линейному закону. Это прямое указание на то, что нельзя пренебрегать конечностью размеров молекул и их взаимодействием. Это и было учтено Ван-дер-Ваальсом.

С ростом p растет плотность газа, и уменьшается среднее расстояние между молекулами. Все более существенной становится конечность размеров т.к. часть объема занимают сами молекулы и он не доступен для их движения.

Для учета собственного объема молекул надо из объема V, занятого газом, вычесть некоторую величину b, пропорциональную собственному объему молекул. Это первая поправка.

Вторая поправка, которую надо ввести в уравнение состояния – это поправка на взаимное притяжение молекул, создающее некоторое дополнительное давление. Тогда уравнение состояния примет вид

Кривая уравнения Ван-дер-Ваальса при невысоких температурах имеет вид (см. рис)

Правая часть участка аб весьма близка к изотерме закона Бойля-Мариотта. Действительно, при большом объеме газа обе поправки в уравнении Ван-дер-Ваальса невелики и левая часть уравнения близка к значению pV. По мере уменьшения объема поправки начинают играть заметную роль. При некотором объеме, которому соответствует точка б на графике, газ при обычных условиях начинает конденсироваться, образуется двухфазная система жидкость - насыщенный пар. Давление насыщенных паров зависит только от температуры, поэтому пока весь пар не превратиться в жидкость, давление изменяться не будет, процесс конденсации изобразится изобарой – прямой БД, параллельной оси абсцисс. Точка д изображает окончание процесса конденсации: весь насыщенный пар превратился в жидкость. Дальнейшее очень незначительное уменьшение объема жидкости может быть получено лишь значительным увеличением давления, поэтому линия де, изображающая жидкое состояние, идет круто вверх. Точки прямой бд, за исключением пересечения ее с кривой вг, не описываются уравнением Ван-дер-Ваальса. Кривая бвгд изображает малоустойчивые состояния вещества.

Начертим изотермы уравнения Ван-дер-Ваальса, снятые при разных температурах. С повышением температуры горизонтальные участки кривых становятся все более короткими и в конце концов линия конденсации исчезает.

Это означает, что исчезает переход из газообразного состояния в жидкое, или наоборот, и, начиная с какой-то температуры, которую обозначим Т_к, состояние вещества становится однофазным. Исчезают фазовые переходы – процесс конденсации и процесс парообразования.

При некоторой температуре, характерной для каждого вещества, исчезает разница между жидким и газообразным состояниями. Это состояние называется критическим состоянием, и температура, при которой оно наступает, носит название критической температуры.