Теорема Кастильяно.

Установим теперь метод определения перемещений, основанный на вычислении потенциальной энергии деформации. Поставим задачу нахождения перемещений точек упругой системы по направлению действия приложенных к этой системе внешних сил.

Будем решать эту задачу в несколько приемов; сначала рассмотрим более простой случай (Рис.1), когда на балку в сечениях 1, 2, 3,... действуют только сосредоточенные силы 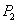, 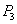)... и т. д. Под действием этих сил балка прогнется по кривой 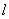и останется в равновесии.

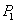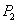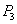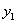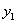Прогибы сечений 1, 2, 3,..., в которых приложены силы , , ,..., обозначим , , ,... и т. д. Найдем один из этих прогибов, например — прогиб сечения, в котором приложена сила .

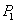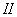Переведем балку, не нарушая равновесия, из положения в смежное положение , показанное на фиг. 328 пунктиром. Это можно сделать различными приемами: добавить новую нагрузку, увеличить уже приложенные и т. д.

Мы представим себе, что для перехода к смежному деформированному состоянию 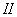к силе 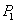сделана бесконечно малая добавка 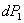(Рис.1); чтобы при этом переходе не нарушать равновесия, будем считать, что эта добавка прикладывается статически, т. е. возрастает от нуля до окончательного значения медленно и постепенно.