Схемы арок, конструкция и расчет
Арки относятся к распорным конструкциям, т. е. для них характерно наличие горизонтальной составляющей опорной реакции (распора).
Арки используются в качестве основных несущих конструкций зданий различного назначения. Их применяют в покрытиях промышленных, сельскохозяйственных и общественных зданий пролетом от 12 до 70 м. В зарубежном строительстве с успехом применяют арки пролетом до 100 м и более.
По статической схеме арки разделяют на трехшарнирные и двухшарнирные без ключевого шарнира:
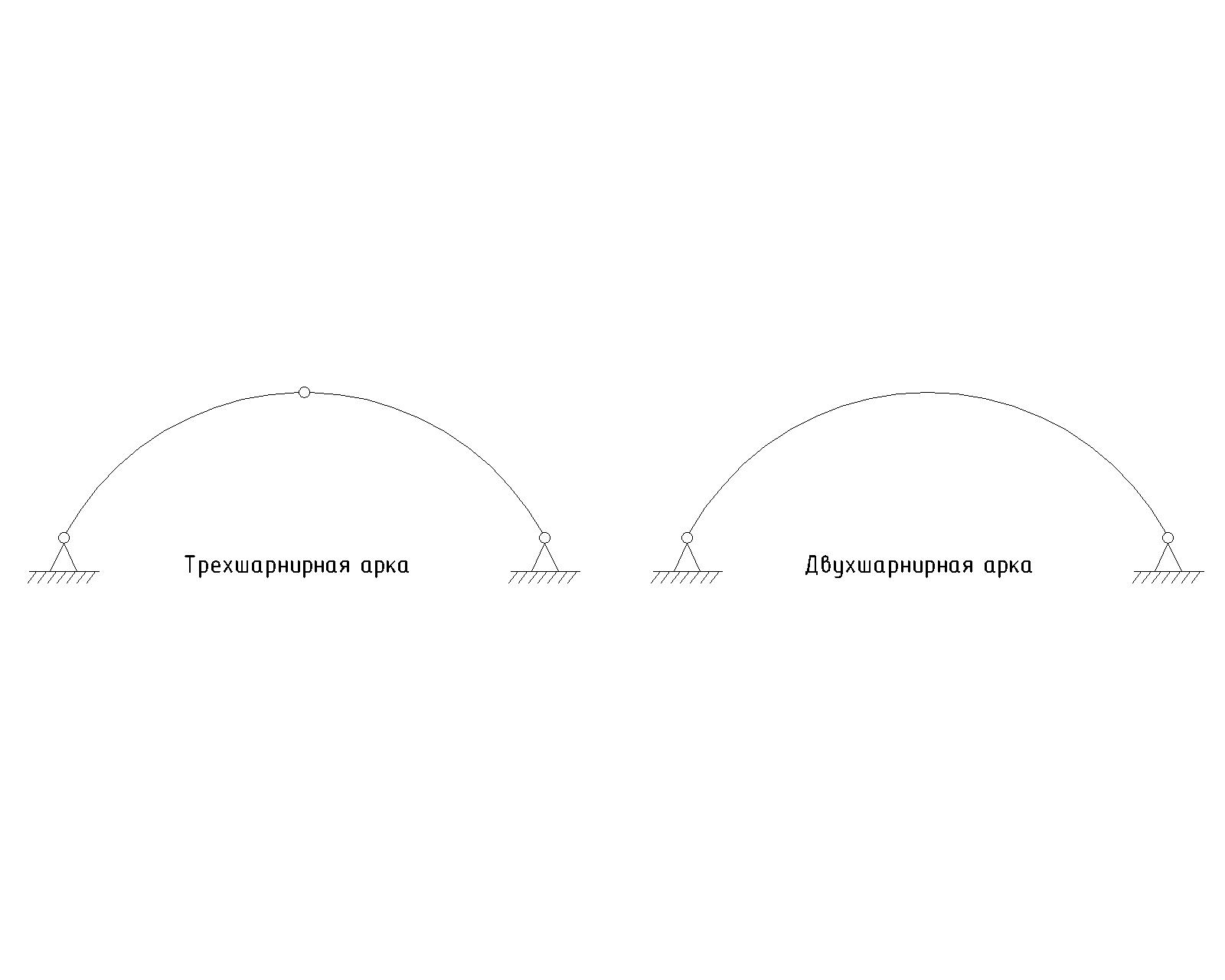
Рисунок 8.1 – Трехшарнирная и двухшарнирная арки
По схеме опирания их делят на арки с затяжками, воспринимающими распор, и на арки без затяжек, распор которых передается на опоры.
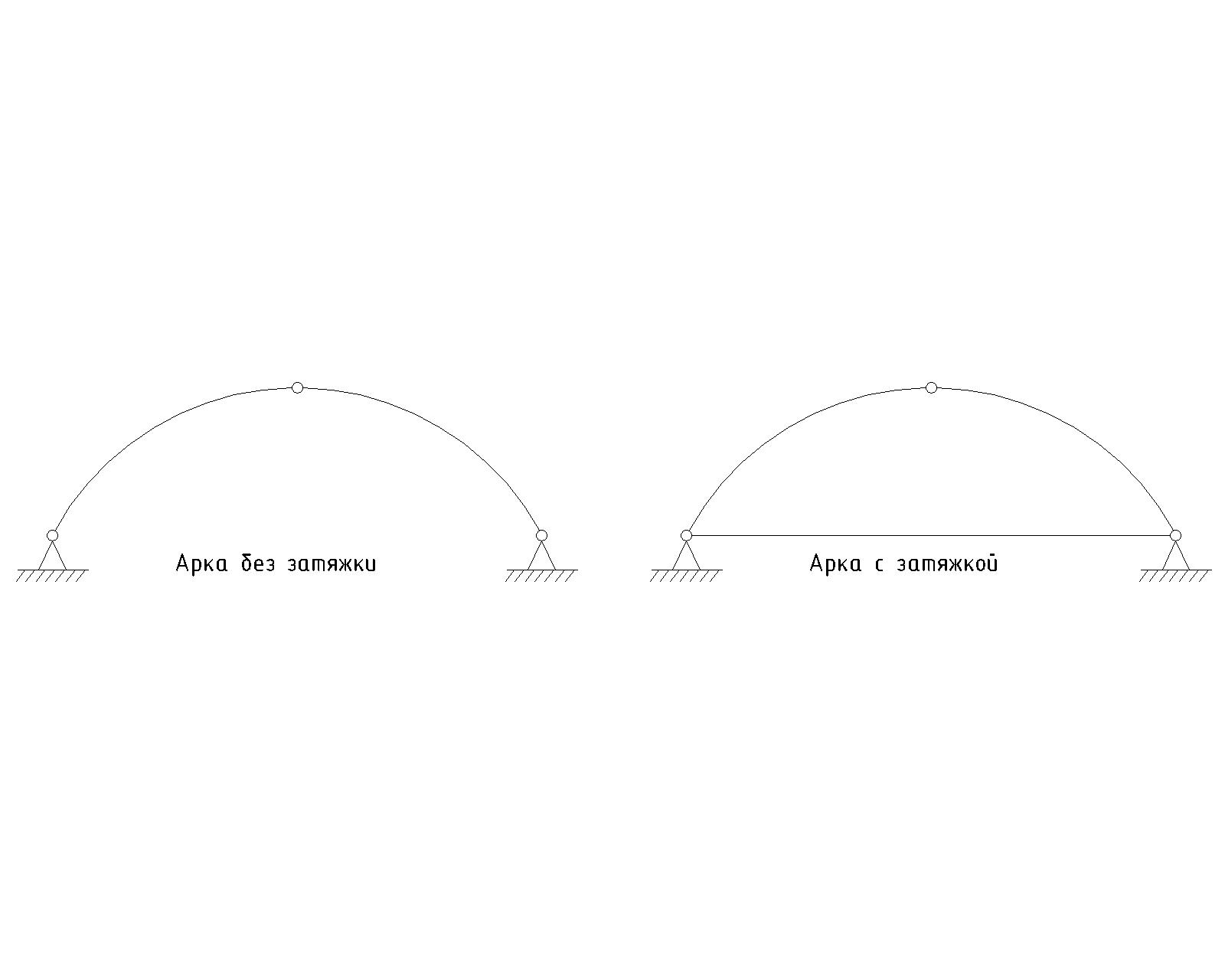
Рисунок 8.2 – Арки без затяжки и с затяжкой
Затяжки изготавливают в большинстве случаев из арматуры или профильной стали. Возможно применение деревянных клееных затяжек, прежде всего в условиях химически агрессивных сред. Дощатоклееные затяжки повышают жесткость арок в процессе транспортирования и монтажа, а также предел огнестойкости.
По форме оси арки делят на:
- треугольные из прямых полуарок;
- пятиугольные;
- сегментные, оси полуарок которых располагаются на общей окружности;
- стрельчатые, состоящие из полуарок, оси которых располагаются на двух окружностях, смыкающихся в ключе под углом.
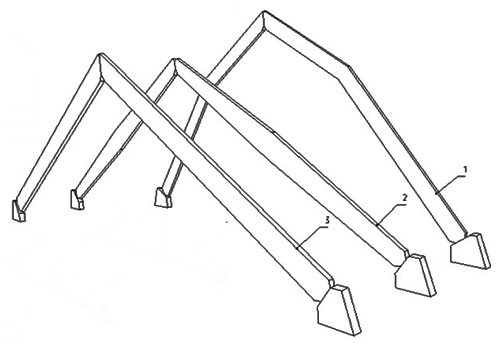
Рисунок 8.3 – Виды арок из прямолинейных элементов:
1 – трехшарнирная ломаного очертания с опиранием на фундамент; 2 – трехшарнирная треугольная переменного сечения с опиранием на фундамент; 3 – трехшарнирная треугольная постоянного сечения с опиранием на фундамент
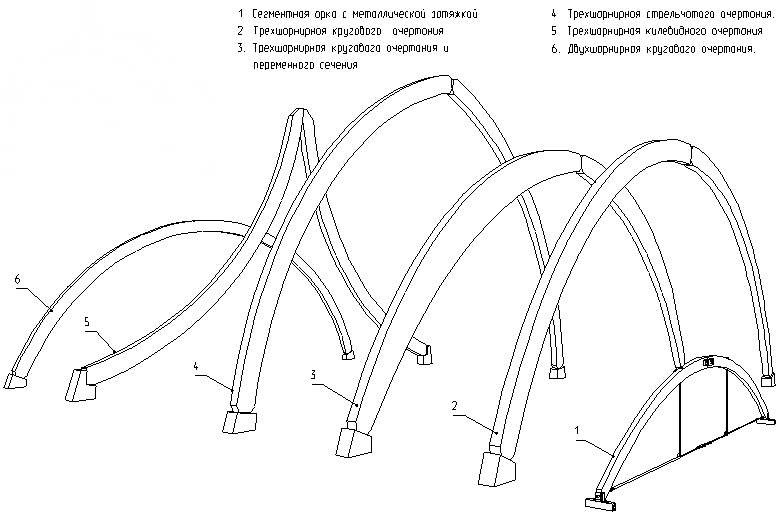
Рисунок 8.4 – Виды арок из криволинейных элементов:
1 – сегментная с металлической затяжкой; 2 – трехшарнирная кругового очертания;
3 – трехшарнирная кругового очертания, переменного сечения; 4 – трехшарнирная стрельчатого очертания; 5 – трехшарнирная килевидного очертания; 6 – двухшарнирная кругового очертания
По конструкции арки делятся на:
1) арки из полуарок цельного сечения (только треугольной формы);
2) арки из ферм;
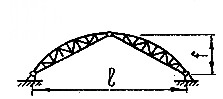
Рисунок 8.5 – Арка из ферм (l=30…60 м, f=l/3…l/2)
3) арки из балок на пластинчатых нагелях (балок Деревягина);
4) кружальные арки, состоящие из двух или более рядов косяков, соединенных между собой нагелями и имеющие смещенные послойно стыки (могут быть кругового или стрельчатого очертания);
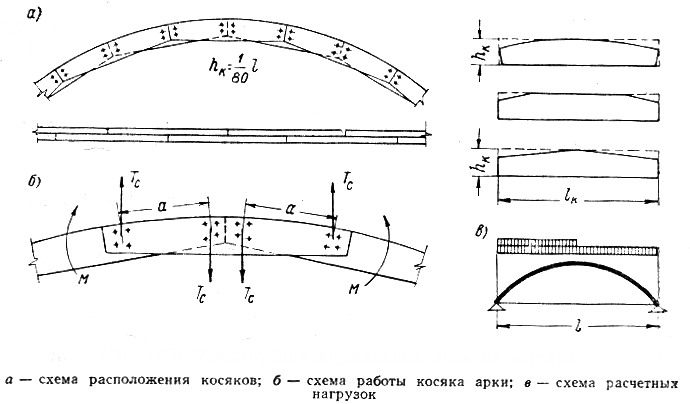
Рисунок 8.6 – Кружальная арка:
а – схема расположения косяков; б – схема работы арки; в – схема расчетных нагрузок
5) арки с перекрестной дощатой стенкой на гвоздях;
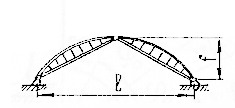
Рисунок 8.7 – Арка с перекрестной дощатой стенкой (l=20…40 м, f≥l/6)
6) клееные арки (дощатоклееные и клеефанерные).
Из перечисленных видов арок наиболее широкое применение получили клееные арки заводского изготовления. Размеры и несущая способность таких арок могут отвечать требованиям сооружения покрытий самого различного назначения, в том числе уникальных по своим размерам.
Арки остальных видов являются конструкциями построечного изготовления и сейчас практически не применяются. Дощатоклееные деревянные арки представляют собой пакет склеенных по пласти досок.
По форме оси дощатоклееные арки могут иметь любой из перечисленных выше видов, т.е. они могут быть треугольными (без затяжек – при высоте 1/2l и с затяжками – при высоте 1/6 … 1/8l в покрытиях до 24 м), пятиугольными с гнутыми участками в местах переломов осей, пологими сегментными двух- или трехшарнирными со стрелой подъема не менее 1/6l (в редких случаях 1/7…1/8l) и высокими трехшарнирными стрельчатыми из элементов кругового очертания со стрелой подъема 1/3…2/3l. Последние два вида клееных арок (сегментные и стрельчатые) рекомендуются в качестве основных.
Поперечное сечение клееных арок рекомендуется принимать прямоугольным и постоянным по всей длине. Высота поперечного сечения назначается 1/30…1/50 пролета. Толщина слоев для удобства гнутья принимается, как правило, не более 1/300 радиуса кривизны и не более 33 мм.
Клеефанерные арки имеют перспективы применения в легких покрытиях. Они, как правило, имеют треугольную форму и состоят из коробчатых клеефанерных полуарок. Такие арки имеют малую массу и позволяют получать существенную экономию древесины. Однако они требуют расхода водостойкой фанеры, являются более трудоемкими при изготовлении, чем дощатоклееные и имеют меньший предел огнестойкости.
Расчет арок
Расчет арок производится по правилам строительной механики, причем распор пологих двухшарнирных арок при стреле подъема не более 1/4 пролета разрешается определять в предположении наличия шарнира в ключе.
Расчет арок после сбора нагрузок выполняется в следующем порядке:
1) геометрический расчет арки;
2) статический расчет;
3) подбор сечений и проверка напряжений;
4) расчет узлов арки.
Нагрузки, действующие на арку, могут быть распределенными и сосредоточенными. Постоянную равномерную нагрузку g от веса покрытия и самой арки определяют с учетом шага арок. Для арок криволинейного очертания она обычно условно считается (в запас прочности), равномерно распределенной по длине пролета, для чего ее фактическое значение умножают на отношение длины арки к ее пролету S/l.
Предварительное определение нагрузки от собственного веса проектируемой арки производится по нижеприведенной формуле в зависимости от ее типа, пролета, и величин нагрузок от собственного веса покрытия gn, снега p и других нагрузок, например нагрузок от подвесного транспортного оборудования
gсв = (gn +p + …)/[1000/(kcвl) - 1]
Коэффициент собственного веса kсв=2…4 при этом следует принимать в зависимости от пролета и величин нагрузок на арку.
Снеговую нагрузку р определяют по приложению 3 СНиП 2.01.07.-85* (схема 1 – для треугольных арок, 2 – для арок кругового очертания, 2/ – для арок стрельчатого очертания).
Сосредоточенные, временные нагрузки Р включают в себя массу подвесного оборудования и временных нагрузок на нем.
Геометрический расчет арки заключается в определении всех размеров, координат сечений, углов наклона касательных к оси в этих сечениях и их тригонометрических функций, необходимых для дальнейших расчетов. Исходными данными при этом являются пролет l, высота f, а в стрельчатых арках также радиус полуарки r или ее высота f.
По этим данным в треугольных арках определяют длину S/2 и угол наклона полуарки α. В сегментных арках определяют радиус r = (l2 +4f)/8, центральный угол φ из условия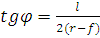 
и длину дуги 
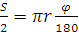полуарки, и находят уравнение дуги в координатах с центром в левой опоре 
.
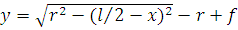В стрельчатых арках определяют угол наклона α и длину l хорды, центральный угол φ и длину S/2 полуарки, координаты центра a и b, угол наклона опорного радиуса φ0 и уравнение дуги левой полуарки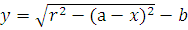 
. Затем половину пролета арки делят на четное число, но не менее шести равных частей и в этих сечениях определяют координаты х и у, углы наклона касательных α к горизонту и их тригонометрические функции.
Статический расчет
Опорные реакции трехшарнирной арки состоят из вертикальных и горизонтальных составляющих. Вертикальные реакции Ra и Rb определяют как в однопролетной свободно опертой балке из условия равенства нулю моментов в опорных шарнирах. Горизонтальные реакции (распор) Ha и Hb определяют из условия равенства нулю моментов в коньковом шарнире.
Определение реакций и усилий удобно производить в сечениях только одной левой полуарки в следующем порядке:
сначала усилия от единичной нагрузки справа и слева, затем от левостороннего, правостороннего снега, ветра слева, ветра справа и массы оборудования.
Изгибающие моменты следует определять во всех сечениях и иллюстрировать эпюрами.
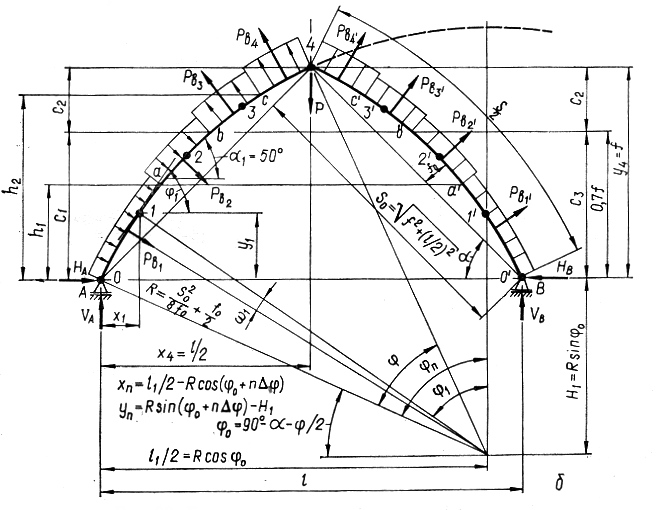
Рисунок 8.8 – Геометрическая и расчетная схема арки
Продольные и поперечные силы можно определять только в сечениях у шарниров, где они достигают максимальных величин и необходимы для расчетов узлов. Необходимо также определять продольную силу в месте действия максимального изгибающего момента при таком же сочетании нагрузок.
Усилия от двусторонней снеговой нагрузки и собственного веса определяют путем суммирования усилий от односторонних нагрузок.
Полученные результаты сводят в таблицу усилий, по которой затем определяют максимальные расчетные усилия при основных наиболее невыгодных сочетаниях нагрузок.
Для клееных арок «Пособие» к СНиП II-25-80 расчет на прочность рекомендует выполнять при следующих сочетаниях нагрузок.
а) в пологих арках (f<1/3l)
– расчетная постоянная и временная (снеговая) нагрузка на всем пролете и временная нагрузка от подвесного оборудования;
– расчетная постоянная нагрузка на всем пролете, односторонняя временная (снеговая) нагрузка на половине пролета и временная нагрузка от подвесного оборудования;
– расчетная постоянная нагрузка на всем пролете, односторонняя временная (снеговая) нагрузка, распределенная по треугольнику на l/2, и временная нагрузка от подвесного оборудования;
б) в стрельчатых арках (f≥1/3l)
- расчетная постоянная и временная (снеговая) нагрузки на всем пролете и временная нагрузка от подвесного оборудования;
- расчетная постоянная нагрузка на всем пролете, временная (снеговая) на S/2 или части пролета в соответствии со СНиП «Нагрузки и воздействия» и временная нагрузка от подвесного оборудования;
- ветровая нагрузка с постоянной и остальными временными (с учетом коэффициентов сочетаний: 0,9 – для кратковременных нагрузок и 0,95 – для длительных).
Максимальные изгибающие моменты возникают обычно в сечениях вблизи четверти пролета арки при действии односторонних временных нагрузок. В треугольных арках моменты от вертикальных нагрузок уменьшаются за счет обратных моментов М от эксцентриситета е продольных сил N.
Наибольшие продольные силы возникают в сечениях вблизи опор, а наибольшие поперечные силы – в сечениях вблизи шарниров.
Усилия в подвесках затяжек возникают от подвешенных к ним грузов и от собственной массы затяжек.
Подбор сечений и проверка напряжений производятся по максимальным значениям расчетных усилий. При этом ветровые нагрузки учитываются только в тех случаях, если ветер более чем на 20 % увеличивает расчетные усилия.
Арки работают на сжатие с изгибом и рассчитываются на прочность и устойчивость в плоскости и из плоскости арки.
Подбор сечений производится методом попыток по величине изгибающего момента при условно пониженном, например, до 0,8Ru расчетном сопротивлении древесины изгибу.
При расчете арок выполняются следующие проверки
1. Проверка прочности по нормальным напряжениям
.
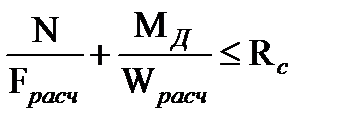2. Расчет на устойчивость плоской формы деформирования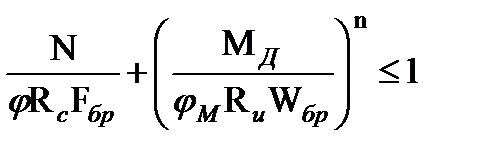 
.
3. Проверка устойчивости в плоскости арки выполняется по формуле
,
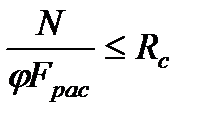где φ=f(λ) – коэффициент продольного изгиба. l=l0/r.
Расчетную длину элемента l0 следует принимать по пункту 6.25 СНиП II-25-80 в зависимости от статической схемы и схемы загружения арки.
При расчете арки на прочность и устойчивость плоской формы деформирования N и Mg следует принимать в сечении с максимальным моментом (Mmax), а расчет на устойчивость в плоскости кривизны и определение коэффициента ξ к моменту Mg нужно определять, подставляя значения сжимающей силы N0 в ключевом сечении арки.
Затяжки и подвески арок работают и рассчитываются на растяжение.
Узлы арок
Основными узловыми соединениями трехшарнирных арок являются опорные и коньковые шарниры.
Опорные узлы арок без затяжек выполняют, как правило, в виде лобовых упоров в сочетании с металлическими башмаками сварной листовой конструкции, служащими для крепления их к опорам.
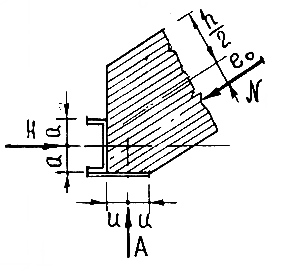
Рисунок 8.9 – Силовые воздействия в опорном узле арки
Башмак состоит из опорного листа с отверстиями для анкерных болтов и двух вертикальных фасонок с отверстиями для болтов крепления полуарок.
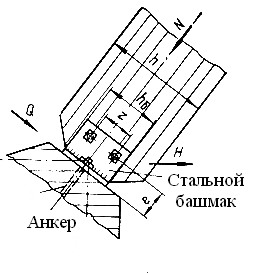
Рисунок 8.10 – Опорный узел
Узлы сегментных и стрельчатых арок, в которых действуют изгибающие моменты разного знака и незначительные поперечные силы, центрируются по осям полуарок, а опорный лист башмака перпендикулярен им.
Узлы треугольных арок, в которых действуют в основном положительные моменты и значительные поперечные силы, центрируются по расчетным осям, расположенным с эксцентриситетом относительно осей полуарок, а опорный башмак перпендикулярен равнодействующей вертикальной и горизонтальной опорных реакций.
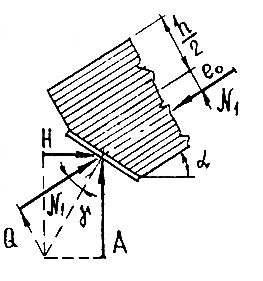
Рисунок 8.11 – Опорная площадка, воспринимающая опорную реакцию без сдвига
Расчет опорного узла заключается в расчете торца полуарки на смятие от действия максимальной сжимающей силы Nсм. В сегментных и стрельчатых арках она равна максимальной продольной силе N и действует вдоль волокон. В треугольных арках она равна равнодействующей опорных усилий
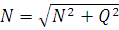
и действует под углом к волокнам α, определяемым из выражения
tga =Q/N.
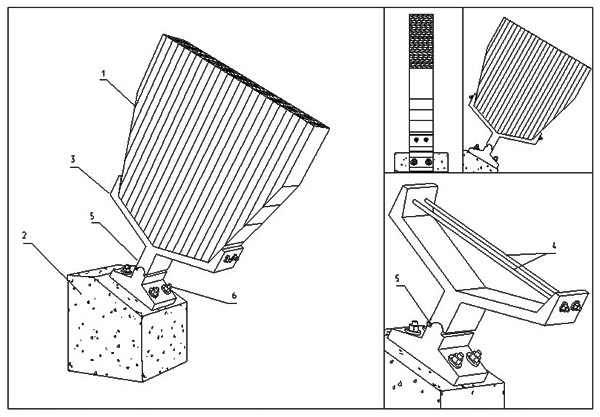
Рисунок 8.12 – Опорный узел с шарниром:
1 – опорная часть дощатоклееной арки; 2 – фундамент; 3 – стальной башмак;
4 – стяжные болты; 5 – цилиндрический шарнир; 6 – анкерные болты
Болты крепления фасонок к полуаркам рассчитывают на действие максимальной поперечной силы Q, как симметрично изгибаемые, двухсрезные. На эту же силу рассчитываются анкерные болты на срез и смятие. Бетон фундамента рассчитывается на смятие от силы Nсм.
Опорный лист башмака работает на изгиб от действия равномерного давления лобового торца полуарки.
Опорные узлы большепролетных арок без затяжек выполняют с применением металлических шарниров качающегося типа (рисунок 8.12).
Опорные узлы клееных арок, работающих в условиях химической агрессии, могут быть выполнены при помощи стержней, одним концом вклеенных в конец полуарки, а другим – заанкерованных в фундамент.
Опорные узлы арок с затяжками
Опорные узлы клееных арок с затяжками выполняются обычно при помощи лобового упора и сварных металлических башмаков несколько иной конструкции.
Опорный лист в арках с затяжками располагается горизонтально, поэтому арки ставятся на горизонтальную поверхность опор, на которые не действует распор. Вертикальные фасонки могут опираться на опорный лист или опорный лист может размещаться между фасонками.
При опирании на бетон опорный лист удлиняют за пределы фасонок для крепления анкеров, а при опирании на деревянную стойку, фасонки опирают ниже опорного листа для крепления их к стойке болтами. Между фасонками располагается упорная диафрагма. Наклон диафрагмы и центрирование узла производятся по тем же соображениям, что и в узлах арок без затяжек.
Металлическую затяжку приваривают к фасонкам, деревянную – располагают между фасонками и крепят к ним болтами.
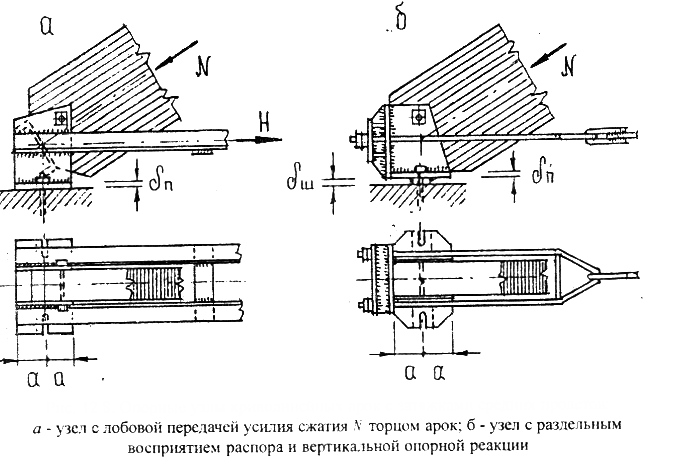
Рисунок 8.13 – Опорный узел с металлической затяжкой:
а – узел с лобовой передачей усилия сжатия N через торец арки; б – узел с раздельным восприятием распора и вертикальной опорной реакции
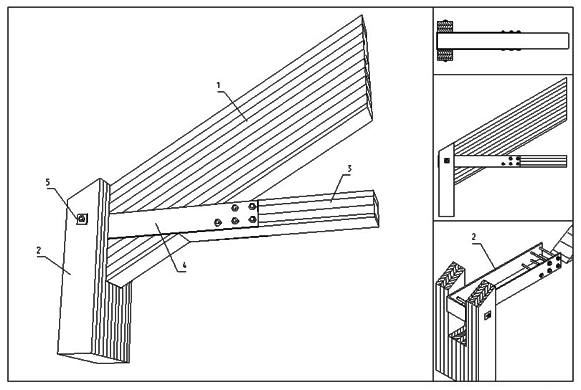
Рисунок 8.14 – Опорный узел с деревянной затяжкой:
1 – верхний пояс дощатоклееной арки; 2 – дощатоклееная стойка; 3 – деревянная затяжка;
4 – хомут из полосовой стали; 5 – стяжной болт с квадратной шайбой
При расчете опорного узла следует выполнить:
1) расчет диафрагмы на изгиб как балки, заделанной в фасонках, на давление лобового упора sд;
2) расчет опорного листа на изгиб как двухконсольной или заделанной в фасонках балки на реактивное давление фундаментов sб;
3) определить длину сварных швов крепления затяжки или число крепежных болтов – для деревянных затяжек из условия восприятия ими усилия в затяжке.
Опорные узлы дощатых арок с затяжками выполняется при помощи гвоздевых или болтовых соединений досок пояса и затяжки.
Затяжки брусчатых арок из арматурной стали пропускаются через отверстия в конце полуарки и закрепляются гайками с шайбами.
Расчет таких узлов производят на смятие торцевых обрезов.
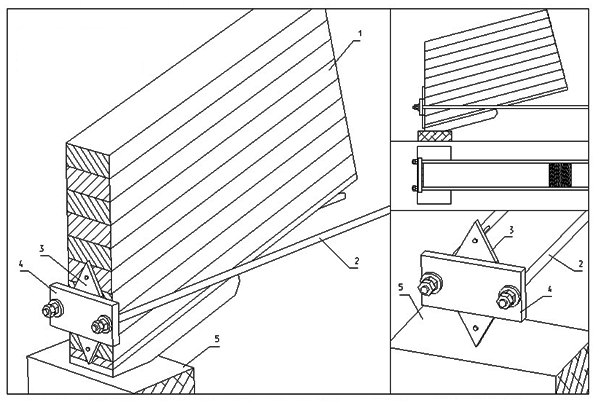
Рисунок 8.15 – Опорный узел арки:
1 – верхний криволинейный пояс дощатоклееной арки; 2 – затяжка из круглой стали;
3 – стальная листовая подкладка переменной жесткости; 4 – стальные накладки; 5 – опора
Коньковые узлы сплошных арок малых и средних пролетов решаются в виде прямых или наклонных лобовых упоров со стальными креплениями или деревянными накладками на болтах. Сегментные и стрельчатые клееные арки центрируются в этих узлах по осям полуарок, а треугольные – с эксцентриситетами (с той же целью, что и в опорных узлах).
Лобовые упоры конькового узла рассчитывают на смятие под углом или вдоль волокон на действие продольной силы N. Количество болтов в стальных креплениях определяется в зависимости от величины поперечной силы Q с учетом угла смятия древесины под болтами. Монтажные болты рассчитывают на срез и смятие от действия той же силы Q.
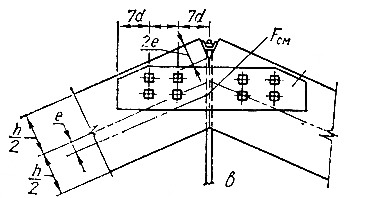
Рисунок 8.16 – Коньковый узел треугольной арки
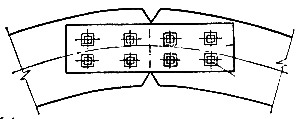
Рисунок 8.17 – Коньковый узел сегментной арки
Коньковые узлы большепролетных арок выполняются в виде стальных шарниров качающегося типа.
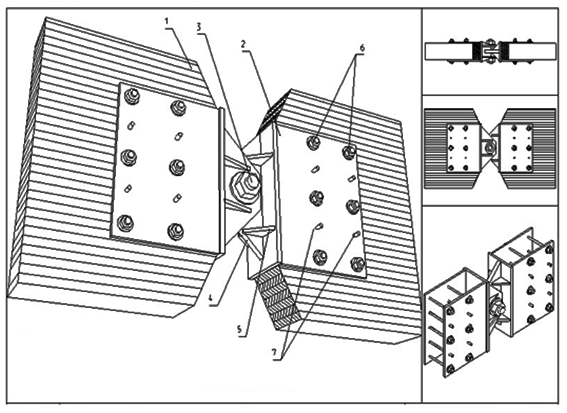
Рисунок 8.18 – Стальной шарнир качающегося типа
1 – верхняя часть полуарки; 2 – боковые накладки стальных сварных башмаков;
3 – болт валикового шарнира; 4 – проушины башмака; 5 – ребра жесткости башмака; 6 – стальные болты с гайками; 7 – стальные нагели
Стыки элементов арок.
Стыки клееных арок представляют собой зубчатые соединения досок по длине и стыки по пласти слоев досок между собой (в арках шириной сечения более 180 мм могут применяться еще и стыки по кромкам). Арки больших пролетов соединяются по длине жесткими стыками с помощью двусторонних накладок из профильной стали и болтов.
Дата добавления: 2015-10-26; просмотров: 28603;