Центр параллельных сил

Зная правила сложения двух параллельных сил, нетрудно путем последовательного сложения найти равнодействующую и для любой системы параллельных сил.

Пусть, например, к телу приложены в точках B₁, В₂ и В₃три параллельные и направленные в одну сторону силы F₁, F₂ и F₃ (рис. 110). Сложив сначала по соответствующему правилу две силы F₁ и F₂, найдем их равнодействующую F₁₂. Складывая затем по тому же правилу силу F₁₂ с силой F₃, найдем равнодействующую F_Σ всех трех данных сил. Эта равнодействующая, очевидно, параллельна данным силам и направлена в ту же сторону.

Модуль равнодействующей равен сумме модулей составляющих сил;

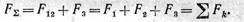
Остается определить положение точки С, через которую проходит линия действия равнодействующей. За точку приложения равнодействующей, конечно, может быть взята любая точка, лежащая на линии ее действия, но оказывается, что только одна из них, именно точка С, определенная путем последовательного сложения сил, обладает особым, весьма важным свойством.

Свойство это состоит в том, что если мы повернем все данные силы вокруг их точек приложения на одинаковый угол, не нарушая их параллельности, то линия действия их равнодействующей, повернувшись на тот же самый угол (как показано на рис. 110 штриховыми линиями), будет вновь проходить через точку С.

Точка С носит название центра системы параллельных сил.

Из сказанного выше следует, что центром данной системы параллельных сил называется точка, через которую проходит линия действия их равнодействующей при любом повороте сил системы вокруг их точек приложения на один и тот же угол в одну и ту же сторону.

Выведем теперь формулы для определения координат центра системы параллельных сил. Возьмем пространственную систему осей координат и обозначим координаты точек приложения данных сил: В₁— соответственно x₁, y ,z₁; В₂— x₂, y₂z₂; B₃ – х₃, у₃, z₃.

Координаты центра параллельных сил С обозначим х_С, у_С , z_С.

Как известно, равнодействующей называется сила, эквивалентная данной системе сил, т. е. равнодействующая приложенная в точке С, производит на тело такое же действие, как и вся система сил F₁, F₂, . . , F_k, . . ., F_n. Значит, согласно теореме Вариньона, момент равнодействующей относительно любой оси равен алгебраической сумме моментов сил относительно той же оси.

Определим моменты сил относительно оси у.

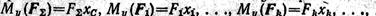
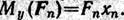
Так как

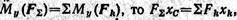
где k принимает последовательно значения от 1 до п.

Отсюда

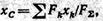
где 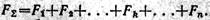Поэтому формула для определения абсциссы центра параллельных сил принимает окончательный вид

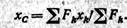
Определив последовательно момент равнодействующей и моменты всех составляющих сил относительно оси х, найдем, что F_Σy_c= ΣF_hy_k, откуда следует формула для определения ординаты центра параллельных сил

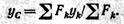
Аналогичную формулу для третьей координаты (аппликаты) центра параллельных сил

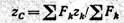
получим, если повернем все силы на 90°, например так, чтобы они расположились параллельно оси у, и определим моменты сил относительно оси х.

Следовательно, формулы координат центра параллельных сил имеют вид

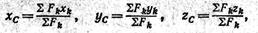
где F_h — модули параллельных сил, x_h, y_k, z_h — координаты точек их приложения.

<50 51 525354 55 56 >

Дата добавления: 2015-09-07; просмотров: 772;