Теоремы о степенях вершин и изоморфизм графов.
Теорема 1: Сумма степеней вершин в неориентированном графе четна и равна удвоенному числу ребер.
Аналогичная теорема может быть сформулирована и для орграфов: сумма полустепеней исхода всех вершин равна сумме их полустепеней захода и равна числу дуг орграфа.
Теорема 2:Число вершин нечетной степени в любом графе четно.
Два графа G1 и G2 называются изоморфными, если существует биективное отображение между множествами их вершин и ребер такое, что соответствующие друг другу по этому отображению ребра графов G1 и G2 инцидентны соответствующим друг другу по этому же отображению парам вершин этих графов.
Согласно определению, графы, изображенные на рисунке 13, изоморфны. Соответствие между множествами вершин и ребер таково:
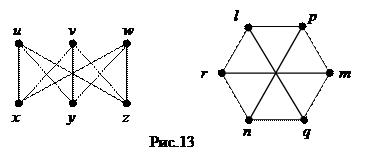 |
для вершин: 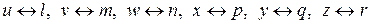
для ребер: 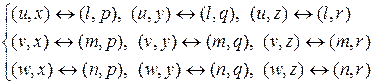
Дата добавления: 2015-10-19; просмотров: 3473;
