Определим потенциальную энергию тела массой m, находящегося на небольшой высоте h над земной поверхностью.

Е_п = - fMm/(R + h) = - f(Mm/R)/(1 + h/R), где

М – масса Земли, R – радиус Земли. Так как h/R <<1, то пренебрегая h²/R² по сравнению с 1, можно считать

1/(1 + h/R) = (1 – h/R)/(1 – h²/R²) » 1 – h/R.

Тогда

Е_п = -fMm(1 – h/R)/R = - fMm/R + (fM/R²)mh, но fM/R² = g,

Тогда

W_п = - fMm/R + mgh,

где fMm/R – потенциальная энергия тела, находящегося на уровне земной поверхности, обычно принимают равной нулю, тогда

Е_п = mgh.

Механическая энергия является лишь одним из многих видов энергии. В настоящее время кроме мех. энергии известны химическая, электрическая, электромагнитная, ядерная, тепловая и др. В природе и технике постоянно имеют место переходы (превращения) энергии из одних видов в другие. Примеры ....

Следует отметить подробность, которую мы позже рассмотрим детальнее, что при любых превращениях энергии некоторая ее часть непременно превращается в теплоту.

Закон сохранения и превращения энергииприменительно к любым ее видам был сформулирован в результате обобщения опытных фактов, но может быть получен и как следствие из законов механики Ньютона.

Полная энергия системы Е складывается из всех присущих системе видов энергии. Опыт показывает, что какие бы превращения энергии не происходили в изолированной системе, полная энергия изолированной системы остается постоянной:

Е = const

(закон сохранения и превращения энергии). При этом будучи несозидаемой и неуничтожаемой, энергия может превращаться из одних видов в другие.

В этой формулировке отражены основные свойства энергии – количественная неизменность и качественная изменчивость.

Применительно к неизолированным системам этот закон формулируется так: изменение энергии неизолированной системы равно работе, совершаемой системой:

DЕ = - А.

Если работа совершается внутренними силами самой системы, то А>0 и энергия убывает. Если же работа совершается внешними силами над системой, то A<0 и энергия системы возрастает.

Закон сохранения и превращения энергии является всеобщим законом природы, не имеющим исключений.

В качестве примера можно рассмотреть применение закона сохранения и превращения энергии и импульса к центральному удару двух абсолютно упругих шаров. Шары летят навстречу др. др. (сделать в качестве домашнего упражнения)

11. ГАРМОНИЧЕСКОЕ КОЛЕБАНИЕ И ЕГО ХАРАКТЕРИСТИКИ.

Среди явлений природы мы часто наблюдаем периодические процессы. Пример: морские приливы и отливы, морские ветры и т.д.

В периодическом процессе изменение какой-либо величины повторяется в точности через совершенно определенное время –период. Математически функция f(t) является периодической с периодом Т, если для любого момента времени выполняется равенство:

F(t + T) = f(t). (1)

Многие реальные процессы идут с «затуханием» и любую величину, описывающую их движение, нельзя в точности описать с помощью (1), т.е. движение не будет периодическим. Однако, движение такого рода, когда тело поочередно многократно раз смещается то в одну то в другую сторону, наз. колебательным движением или колебанием. Периодические процессы представляют частный случай колебательных процессов. Их можно представить как наложение гармонических колебаний.

Фурье анализ.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему.

Несмотря на большое разнообразие колебательных процессов, все они совершаются по некоторым общим закономерностям и могут быть сведены к совокупности простейших периодичесих колебаний, называемых гармоническими. Эти колебания представляют собой периодический процесс, в котором изменение какой-либо величины происходит по закону синуса или косинуса.

Ознакомимся с этими колебаниями на примере равномерного движения материальной точки по окружности.

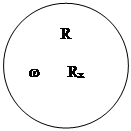
Предположим материальная точка А движется по окружности радиуса R c угловой скоростью w. Смещение ее вдоль оси Ох будет определяться проекцией радиуса на ось Ох (рис.1)

Y

Рис.1.

A

X

R_x(t) = R cos ( wt + j ). (2)

Эта формула описывает колебательное движение проекции точки А вдоль оси Ох около точки О, которую будем наз. «положением равновесия».Период изменения проекции такой же, как и время одного оборота точки А. Он равен Т = 2p¤w. (wt + j) - фаза колебания (аргумент тригонометрической функции в уравнении гармонических колебаний). Она определяет состояние колебательной системы в любой момент времени. При t = 0 j₀ – начальная фаза.

Максимальное значение проекции точки А вдоль оси Ох от положения равновесия, наз амплитудой колебаний. В данном случае R_xmax. = R. Очевидно, фазам, различающимся между собой на величину кратную 2p, соответствуют одинаковые смещения. Изменение фазы на 2p рад. соответствует промежутку времени в период Т.

Обычно смещение обозначают X и тогда

X(t) = A sin (wt + j₀) (2¢).

Определим скорость точки, совершающей гармоническое движение

V = dx/dt = wAcos wt =wA sin(wt + p /2). (3)

Из (3) видно, что V = V(t), следовательно, колебательное движение совершается с ускорением W, которое равно

W =d²x/dt² =dV/dt=w²Acos(wt + p/2)=w²A sin(wt +p)= - w²Asinwt= -w²x. (4).

Из выражения (4) следует дифференциальное уравнение гармонических колебаний

d²x/dt² + w²x = 0.

Решением этого уравнения является уравнение (2¢).

Таким образом, смещение X, скорость V и ускорение W точки Асовершают гармонические колебания с одинаковыми круговой частотой и периодом Т = 2p¤w.

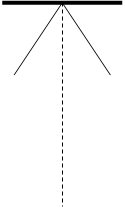
В качестве примера гармонических колебаний рассмотрим движение математического маятника, т.е. небольшого тела, подвешенного на столь длинной нити, что размерами тела по сравнению с длиной нити можно пренебречь. Нить нерастяжима и невесома.

a

`T

A

A^¢

· O

m`g m`g

Рис.2.

Если отклонить тело от положения равновесия (в точку А) и отпустить, оно начнет совершать колебательные движения, рис.2. На тело действуют сила тяжести и сила натяжения нити. Составляющая силы тяжести mgsina,направлена вдоль касательной к траектории, меняет величину скорости тела. Маятник движется вниз с нарастающей скоростью.

По второму закону Ньютона

- mg sina = mW_t (*)

Cчитаем: a>0 и х>0 при отклонениии вправо от вертикали.

В положении равновесия (в точке 0) касательное ускорение W_t =0, однако скорость тела не равна нулю, и оно по инерции движется дальше, поднимаясь вверх. Слева от положения равновесия тангенциальная составляющая силы тяжести направлена против скорости, следовательно, движение маятника замедляется. В момент остановки (точка А¢) скорость V = 0, a ускорение W_t = max и маятник начнет двигаться направо в сторону положения равновесия.

Если угол отклонения a мал, то отклонение тела от положения равновесия х, отсчитываемое вдоль дуги окружности, по которой движется маятник, равно х = al. Уравнение Ньютона (*) тогда будет иметь вид

ga = - W_t.

Знак «-« означает, что угол a и ускорение направлены в разные стороны. Т.к. a =х/l, то

W_t = - gx/l (5)

Сравниваем (5) и (4) и видим, что w² = g/l, т.е. движение маятника происходит по гармоническому закону, а его смещение в любой момент времени определяется выражением

X(t) = Asin(Ö g/l + j₀), т.е.

Математический маятник колеблется с частотой w=Ög/l, а его период

Т = 2p¤w = 2p¤Ög/l = 2pÖl/g ¹ f(m) ! ® g !

Аналогично рассматриваются колебания пружинного маятника и получают:

X(t) = A sin(Ök/m t + j₀) ,

а период T = 2p¤w = 2pÖm/k, где к – жесткость.

При гармоническом колебании происходит взаимное превращение кинетической энергии колеблющегося тела Е_к и потенциальной энергии Е_п, обусловленной действием квазиупругой силы. Полная энергия:

Е = Е_к + Е_п, но

Е_k = mV²/2 = (m/2)w²A²sin²(wt + p/2) = (m/2)w²A²cos²wt,

E_п = kx²/2 = (k/2)A²sin²wt, но из F = mW = -mw²x = -kx имеем к=mw²

Поэтому Е_п = (m/2)w²A²sin²wt.

Полная механическая энергия колеблющегося тела

Е = Е_п + Е_к = (m/2) w²A²(cos²wt + sin²wt) = m²A²w²/2

(незатухающих свободных колебаний) не изменяется с течением времени и равна ее запасу, сообщенному телу в начальный момент времени, при выведении его из положения равновесия. В процессе колебаний происходит только превращение видов энергии из кинетической в потенциальную и обратно с частотой, вдвое большей частоты колебаний, Е ~ w² и Е ~ А². (Е = кХ²/2, Т = 2pÖ m/k).

В реальных свободных затухающих колебаниях их энергия, как и амплитуда, с течением времени непрерывно уменьшаются, расходуясь на преодоление сил тяжести.