Вероятностный подход. Вероятностный подход используется в теории информации.
Вероятностный подход используется в теории информации.
Пусть имеется какое-либо событие или процесс, это может быть опыт с бросанием игральной кости, вытаскивание шара определенного цвета из коробки, получение определенной оценки и т.п. Введем обозначения:
P – вероятностьнекоторогособытия
n – общее число возможных исходов данного события
k – количество событий из всех возможных, когда происходит событие
I – количество информациио событии
Тогда вероятность этого события равна P=k/n
А количество информации о нем выражается формулой: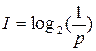
(вспомним, что логарифм определяет степень, в которую нужно возвести основание логарифма, чтобы получить аргумент)
Пример: испытание – подбрасывание игральной кости (кубика), событие – выпадение чётного количества очков. Тогда n=6, k=3, P=3/6=1/2,
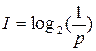=log2(2)=1
При рассмотрении вопроса о количестве информации I, вводят понятие неопределенности состоянии системы – энтропии системы (H). Получение информации о какой-либо системе всегда связано с изменением степени неосведомленности получателя о состоянии этой системы.
Энтропия системы, имеющей n возможных состояний, когда различные исходы опыта неравновероятны (например, получение положительной оценки на экзамене – вероятность получения 3, 4 или 5 разная) вычисляется по формуле:
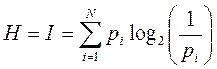, где Pi – вероятность i-го исхода.
Это выражение называется формулой Шеннона.
Частный случай формулы Шеннона это формула Хартли, когда события равновероятны:
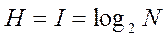
То есть нужно решить показательное уравнение относительно неизвестной I: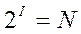 
.
Важным при введении какой-либо величины является вопрос о том, что принимать за единицу ее измерения. Из формулы Хартли следует, что H=I=1 при N=2 (21=2). Иными словами, в качестве единицы принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (примером такого опыта может служить бросание монеты, при котором возможны два исхода: «орел», «решка»). Такая единица количества информации называется - бит. Сообщение, уменьшающее неопределенность знаний человека в два раза, несет для него 1 бит информации.
Рассмотрим примеры на подсчет количества информации.
Пример 1. В барабане для розыгрыша лотереи находится 32 шара. Сколько информации содержит сообщение о первом выпавшем номере (например, выпал номер 15)? Поскольку вытаскивание любого из 32 шаров равновероятно, то количество информации об одном выпавшем номере находится из уравнения:
Решение. По формуле Хартли I=log232, следовательно, количество информации I равняется числу, в которое нужно возвести 2, чтоб получить 32 – это 5, так как 25=32.
Ответ. I=5 бит.
Пример 2. В коробке имеется 50 шаров. Из них 40 белых и 10 черных. Определить количество информации в сообщении о выпадании белого шара и черного шара.
Решение. Обозначим pч – вероятность вытаскивания черного шара, pб - вероятность вытаскивания белого шара. Тогда
pч = 10/50 = 0,2; pб = 40/50 = 0,8.
Теперь, зная вероятности событий, можно определить количество информации в сообщении о каждом из них, используя формулу I=log2(1/p):
Iч = log2 (1/0,2) = log2 5 = 2,321928;
Iб = log2 (1/0,8) = log2 (1,25) = 0,321928.
Дата добавления: 2015-10-19; просмотров: 1273;