Алгоритм электронной цифровой подписи RSA

Первой и наиболее известной во всем мире конкретной системой ЭЦП стала система RSA, математическая схема которой была разработана в 1977 г. в Массачуссетском технологическом институте США.

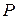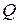Сначала необходимо вычислить пару ключей (секретный ключ и открытый ключ). Для этого отправитель (автор) электрон­ных документов вычисляет два больших простых числа и , затем находит их произведение 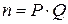и значение функции Эйлера 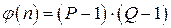. Далее отправитель вычисляет число К₀ из условий: 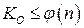, НОД 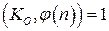и число К_с из условий: , .

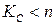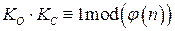Пара чисел (К₀,n) является открытым ключом. Эту пару чисел автор передает партнерам по переписке для проверки его цифровых подписей. Число К_с сохраняется автором как секретный ключ для подписывания. Обобщенная схема формирования и проверки цифровой подписи RSA показана на рис. 7.9.

Допустим, что отправитель хочет подписать сообщение 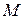перед его отправкой. Сначала сообщение 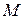(блок информации, файл, таблица) сжимают с помощью хэш-функции 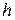в целое число 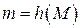. Затем вычисляют цифровую подпись 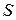под электронным докумен­том 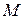, используя хэш-значение 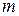и секретный ключ : .

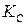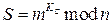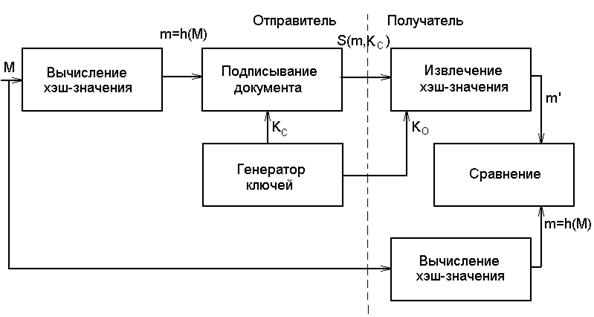Рис. 7.9. Обобщенная схема алгоритма ЭЦП RSA

Пара 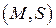передается партнеру-получателю как электрон­ный документ 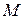, подписанный цифровой подписью 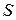, причем подпись 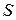сформирована обладателем секретного ключа К_c. После приема пары 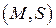получатель вычисляет хэш-значение сообщения 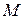двумя разными способами. Прежде всего он восстанавливает хэш-значение 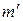, применяя криптографическое преобразование подписи 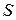с использованием открытого ключа К₀: 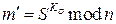. Кроме того, он находит результат хэширования принятого сообще­ния 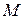с помощью такой же хэш-функции 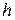: 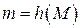. Если соблюдается равенство вычисленных значений, т. е. 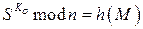, то получатель признает пару 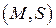подлинной. Доказано, что только обладатель секретного ключа К_c может сформировать цифровую подпись 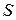по документу 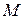, а определить секретное число К_c по открытому числу К₀ не легче, чем разложить модуль 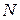на множители. Кроме того, можно строго математически доказать, что ре­зультат проверки цифровой подписи 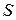будет положительным только в том случае, если при вычислении 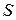был использован секретный ключ К_c, соответствующий открытому ключу К₀. Поэтому открытый ключ К₀ иногда называют «идентификатором» подпи­савшего.

Недостатками алгоритма цифровой подписи RSA являются:

1. При вычислении модуля 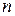ключе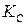й и 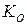для системы цифровой подписи RSA необходимо проверять большое количе­ство дополнительных условий, что выполнить практически трудно. Невыполнение любого из этих условий делает возможным фаль­сификацию цифровой подписи со стороны того, кто обнаружит та­кое невыполнение при подписании важных документов, а такую возможность нельзя допускать даже теоретически.

2. Для обеспечения криптостойкости цифровой подписи RSA по отношению к попыткам фальсификации на уровне, напри­мер, национального стандарта США на шифрование информации (алгоритм DES), т. е. 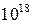, необходимо использовать при вычисле­ниях 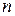, К_с и К₀ целые числа не менее 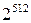(или около 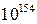) каж­дое, что требует больших вычислительных затрат, превышающих на 20…30 % вычислительные затраты других алгоритмов циф­ровой подписи при сохранении того же уровня криптостойкости.

3. Цифровая подпись RSA уязвима к так называемой муль­типликативной атаке. Иначе говоря, алгоритм цифровой подписи RSA позволяет злоумышленнику без знания секретного ключа К_с сформировать подписи под теми документами, у которых резуль­тат хэширования можно вычислить как произведение результатов хэширования уже подписанных документов.