Составление вариационных рядов
Группа чисел, объединяемая каким-либо признаком, называется совокупностью.
Как было отмечено выше, первичный статистический спортивный материал представляет собой группу разрозненных чисел, не дающих тренеру представления о существе явления или процесса. Задача заключается в том, чтобы превратить эту совокупность в систему и воспользоваться ее показателями для получения требуемой информации.
Составление вариационного ряда как раз и представляет собой формирование определенной математической
Пример 2. У 34 спортсменов-лыжников зарегистрировано такое время восстановления пульса после прохождения дистанции (в секундах):
81; 78: 84; 90; 78; 74; 84; 85; 81; 84: 79; 84; 74; 84; 84;
85; 81; 84; 78: 81; 74; 84; 81; 84; 85; 81; 78; 81; 81; 84;
84; 84; 78; 81.
Как видно, данная группа цифр не несет никакой информации.
Для составления вариационного ряда вначале производим операцию ранжирования — расположения чисел в порядке возрастания или убывания. Например, в порядке возрастания ранжирование приводит к следующему;
74; 74; 74; 74;
78; 78; 78; 78; 78; 78;
81; 81; 81; 81; 81; 81; 81; 81; 81;
84; 84; 84; 84; 84; 84; 84; 84; 84; 84; 84;
85; 85; 85;
90.
В порядке убывания ранжирование приводит к такой группе чисел:
90;
85; 85; 85;
84; 84; 84; 84; 84; 84; 84; 84: 84: 84; 84;
81; 81; 81; 81; 8!; 81: 81; 81; 81;
78; 78; 78; 78; 78; 78;
74; 74; 74: 74.
После проведения ранжирования становится очевидной нерациональная форма записи данной группы чисел—одни и те же числа повторяются многократно. Поэтому возникает естественная мысль преобразовать запись таким образом, чтобы указать, какое число сколько раз повторяется. Например, учитывая ранжирование в порядке возрастания:
74—4;
78—6;
81—9;
84—11;
85—3;
90—1
Здесь слева записано число, указывающее время восстановления пульса спортсмена, справа—число повторений этого показания в данной группе из 34 спортсменов.
В соответствии с приведенными выше понятиями о математических символах рассмотренную группу измерений обозначим какой-либо буквой, например х. Учитывая возрастающий порядок чисел в данной группе: х1 —74 с; х2 — 78 с; х3 — 81 с; х4 — 84 с; х5— 85 с; х6—хn — 90 с, каждое рассмотренное число можно обозначить символом Xi.
Обозначим число повторений рассмотренных измерений буквой n. Тогда:
n1=4; n2=6; n3=9; n4=11; n5=3;n6=nn=1, а каждое число повторений можно обозначить как ni.
Общее число проведенных измерений, как следует из условия примера, есть 34. Это означает, что сумма всех n равна 34. Или в символическом выражении:
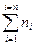 = 34
= 34
Обозначим эту сумму одной буквой — n. Тогда исходные данные рассматриваемого примера можно записать в таком виде (табл. 1).
Полученная группа чисел есть преобразованный ряд хаотически рассеянных показаний, полученных тренером в начале работы.
Таблица 1
| хi | ni |
| n=34 |
Такая группа представляет собой определенную систему, параметры которой характеризуют проведенные измерения. Числа, представляющие собой результаты измерений (хi), называют вариантами; ni — числа их повторений — называются частотами; n — сумма всех частот — есть объем совокупности.
Вся полученная система называется вариационным рядом. Иногда эти ряды называются эмпирическими или статистическими.
Нетрудно заметить, что возможен частный случай вариационного ряда, когда все частоты равны единице ni ==1, то есть каждое измерение в данной группе чисел встретилось только один раз.
Полученный вариационный ряд, как и всякий другой, можно представить графически. Для построения графика полученного ряда, необходимо прежде всего условиться о масштабе на горизонтальной и вертикальной оси.
В данной задаче на горизонтальной оси будем откладывать значения времени восстановления пульса (х1) таким образом, что единице длины, избранной произвольно, соответствует значение одной секунды. Откладывать эти значения начнем с 70 секунд, условно отступая от места пересечения двух осей 0.
На вертикальной оси отложим значения частот нашего ряда (ni), принимая масштаб: единица длины равна единице частоты.
Подготовив таким образом условия для построения графика, приступаем к работе с полученным вариационным рядом.
Первую пару чисел х1=74, n1=4 наносим на график так: на оси х; находим х1=74 и восстанавливаем перпендикуляр из этой точки, на оси n находим n1=4 и проводим из нее горизонтальную линию до пересечения с восстановленным прежде перпендикуляром. Обе линии—вертикаль и горизонталь—являются линиями вспомогательными и потому наносятся на рисунок пунктиром. Точка их пересечения представляет собой в масштабе данного графика соотношение Х1=74 и n1=4.
Таким же образом наносятся все остальные точки графика. Затем они соединяются отрезками прямых. Для того чтобы график имел замкнутый вид, крайние точки соединяем отрезками с соседними точками горизонтальной оси.
Полученная фигура есть график нашего вариационного ряда (рис. 1).
Совершенно понятно, что каждый вариационный ряд представляется своим собственным графиком.
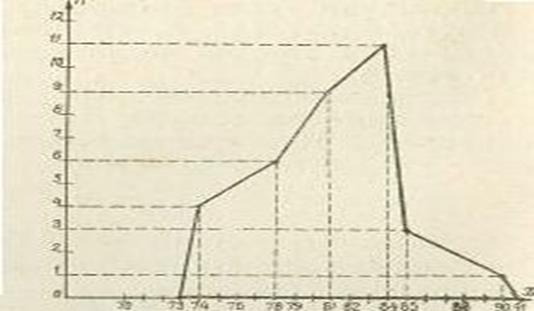
Рис. 1. Графическое представление вариационного ряда.
На рис. 1 видно:
1) из всех обследованных наибольшую группу составили спортсмены, время восстановления пульса у которых 84 с;
2) у многих это время 81 с;
3) наименьшую группу составили спортсмены с малым временем восстановления пульса — 74 с и большим — 90 с.
Таким образом, выполнив серию испытаний, следует ранжировать полученные числа и составить вариационный ряд, представляющий собой определенную математическую систему. Для наглядности вариационный ряд можно иллюстрировать графиком.
Приведенный выше вариационный ряд называется еще дискретным рядом — таким, у которого каждый вариант выражен одним числом.
Приведем еще несколько примеров на составление вариационных рядов.
Пример 3. 12 стрелков, выполняя упражнение лежа из 10 выстрелов, показали такие результаты (в очках):
94; 91; 96; 94; 94; 92; 91; 92; 91; 95; 94; 94.
Для образования вариационного ряда произведем ранжирование данных чисел;
91; 91; 91;
92; 92;
94; 94; 94; 94; 94;
95;
96.
После ранжирования составляем вариационный ряд (табл. 3).
Таблица 3
| хi | ni |
| n=12 |
Пример 4. Баскетбол. 26 школьников выполняют броски в корзину. Каждый школьник из 12 попыток, предоставленных ему в течение урока, забросил мяч столько раз:
7; 9; 10; 6; 0; 8;
8; 10; 0; 7; 9; 4;
2; 9; 8; 12; 5; 5;
0; 6; 9; 6; 8; 10; 2;
Ранжирование в данном примере выглядит следующим образом:
0; 0; 0;
2; 2;
4;
5; 5;
6; 6; 6;
7; 7;
8; 8; 8; 8;
9; 9; 9; 9; 9;
10; 10; 10;
12.
На основании этого вариационный ряд будет таким (табл. 4).
| Таблица 4 | |
| хi | ni. |
| n=2б |
При достаточном навыке и небольшом числе измерений операцию ранжирования можно делать устно, составляя вариационный ряд непосредственно из исходных данных.
Дата добавления: 2015-10-19; просмотров: 23186;
