Некоторые математические символы

Как известно, элементарная математика оперирует цифрами, в то время как высшая математика пользуется буквенными выражениями. Это объясняется тем, что высшая математика рассматривает более общие процессы и явления и в более сложном их проявлении-

В частности, математическая статистика также использует буквенные символы. Их значение рассмотрим на таком примере.

Пример 1. В соревнованиях спортсмены показали определенные результаты:

4.02; 4.04; 4.05; 4.08; 4.10 — время велосипедистов II разряда на дистанции 3 км (мужчины);

11,8; 12,0; 12,3—время в беге на 100 м (женщины) ;

69,40; 70,12; 71,20; 74,00—результат копьеметателей I разряда (мужчины).

Как видно из примера, каждая группа чисел представляет собой определенные показатели, качественно отличающиеся друг от друга.

Обозначим каждую группу чисел каким-либо одним символом (предпочтительней всего буквой латинского алфавита). Например, результаты велосипедистов обозначим символом х, бегунов — у, а копьеметателей — z. Тогда, не прибегая к подробному перечислению всех чисел в каждой группе, можно оперировать только символами. Можно сказать: «сложить все х», вместо подробной записи 4.02+4.04+4.05+4.08+4.10; «разделить все z на 5» и т. д. Как видно из примера, из простого удобства это превращается в необходимость, если в каждой группе содержится много чисел.

Порядковое место каждого числа в одной группе обозначается числовым индексом возле буквы. Так, по­казания велосипедистов можно записать символически:

4.02 есть x₁, поскольку 4.02 это число, которое относится к группе, обозначенной символом х, и стоящее в этой группе на первом месте; 4.04 есть x₂, стоящее на втором месте; 4.05 есть x₃. 4.08 — x₄; 4.10—х₅. Показания бегунов будут выглядеть как 11,8—у₁ 12,0—у₂; 12,3—у₃; т. к. они соответственно стоят на первом, втором и третьем порядковых местах. Наконец, результаты копьеметателей обозначим 69,40—z_1, 70,12—z₂, 71,20—z₃; 74,00 — z₄.

Существуют также и буквенные индексы. Из них самыми распространенными являются индексы «i» и «n».

Индекс «i» дословно означает: любой, имеющий вообще какой-либо порядковый номер. Например, z_i означает—любое число из группы z. В приведенном примере z_i есть и z₁=69,40, и z₂=70,12, и z₃=71,20, z₄== 74,00.

Индекс «n» означает — последнее по порядку число, стоящее в данной группе. Так, символ x_n означает число из группы х, стоящее на последнем месте, т. е. в нашем примере—это пятое число х_n=x₅=4.10.

Если необходимо сложить числа одной группы, употребляют знак сложения ∑ (сигма, заглавная печатная буква греческого алфавита).

Справа от знакa ∑ стоит символ той группы чисел, которая подлежит сложению. Например, ∑х₁ означает сложить числа группы х.

На нижнем горизонтальном участке символа ∑ следует записать индекс того числа, с которого начинают сложение, на верхнем—индекс числа, которым сложение заканчивают. Например,

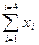
обозначает: сложить все числа группы х от первого до четвертого включительно.

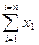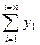Сумма, записанная в виде символа или может быть подвергнута дальнейшим операциям как единое число.

Например, сумму показателей всех бегунов нужно разделить на число К. Символически это можно записать так:

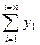
К

Или сумму результатов копьеметателей нужно умножить на число С:

С ∙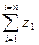

Очевидно, что при большом количестве чисел символическая запись позволяет просто и удобно оперировать ими.

Следует отметить, что при выборе букв для символов и индексов (кроме постоянного знака ∑) исследователь не связан ни с какими ограничениями. Буквы избираются произвольно, хотя предпочтение отдается буквам латинского алфавита, затем—буквам греческого алфавита. Славянский шрифт в обозначении символов, как правило, не употребляют.

Пользуясь вышеприведенными символами, приступим к понятию вариационных рядов.