Дифференциальные уравнения и передаточные функции звеньев и САУ.

При исследовании и расчете САУ исходят из математического описания, происходящих в них процессах. Для линейных САУ широко используется для этой цели операторный метод. Его сущность в том, что исследуемая система разделяется на звенья направленного действия. Совокупность этих звеньев совместно с линиями связи между ними, характеризующими их взаимодействие, образуют структурную схему САР. Они отражают математически динамические свойства системы. Разбиение системы на звенья существенно облегчает их расчет. Процессы, протекающие в САУ, описываются дифференциальными. уравнениями. Задача составления дифференциальных уравнений системы сводится к составлении системы отдельных звеньев. Любое звено автоматической системы предназначено для измерения, усиления или какого-либо другого преобразования сигнала. В связи с этим для любого элемента характерной являются связи между его входным и выходным сигналом. Именно эта связь и может быть представлена дифференциальными уравнением, которое математически выражает физические процессы в звене, т. е. процессы формирования выходного сигнала элемента, при подаче на его вход входного сигнала. Для облегчения исследования сложных систем дифференциальных уравнений, описывающие поведение системы заменяются алгебраическими, с помощью преобразований Лапласа. Если имеется некоторая функция f(t) независимой вещественной переменной t, то преобразование Лапласа, производимое над этой функцией и обращающее ее в функцию F(x), определяются след соотношением

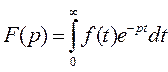
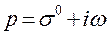
где p-произвольная комплексная величина, имеющая вещественную и мнимую часть. При этом функция f(t) называется оригиналом, а F(p)-изображением функции. Сокращенно преобразования Лапласа обозначаются: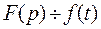

Для линейных звеньев связь между входным и выходным сигналом может быть описана линейным дифференциальным уравнением следующего вида:

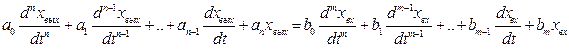
(1)

Воспользовавшись преобразованием Лапласа, дифференциальным уравнением (1) может быть представлено в следующем виде:

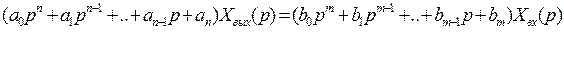
(2)

Левая часть равенства в скобках - выходной операторный полином, правая – входной.

Передаточной функцией звена или системы автоматического управления называется отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины.

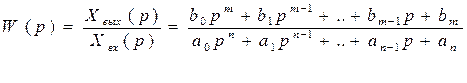
1) При р=0 выражение передаточной функции превращается в коэффициент усиления. W(p)=K.

2) Из выражения передаточной функции видно, что изображение выходной величины равно:

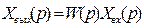
Этим выражением можно пользоваться при определении характера переходных процессов, возникающих в системе, при подаче на ее вход любого произвольно меняющегося входного воздействия. Анализ и синтез систем автоматического управления предполагает предварительное получение информации о виде передаточной функции. Для ряда типовых динамических звеньев передаточные функции являются одинаковыми, отличие может состоять в коэффициенте выражений передаточных функций.