Цепь синусоидального тока с идеальной индуктивностью.

Катушка индуктивности при протекании по ней тока обладает способностью создавать магнитное поле. Это свойство характеризуется параметром катушки, называемым индуктивностью L.

Для удобства анализа работы катушки в цепи переменного тока условно будем считать, что R_K = 0 (идеализированная катушка).

Пусть по катушке с числом витков w протекает ток, изменяющийся по закону I = I_m·sinω·t(начальная фаза принята равной нулю). Этот ток создаёт синусоидальный магнитный поток, мгновенное значение которого равно

где Ф_m – амплитуда потока 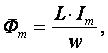а начальная фаза и частота равны начальной фазе и частоте тока.

Напряжение источника и = и_L уравновешивается ЭДС самоиндукции е_Lкатушки

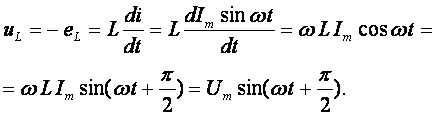
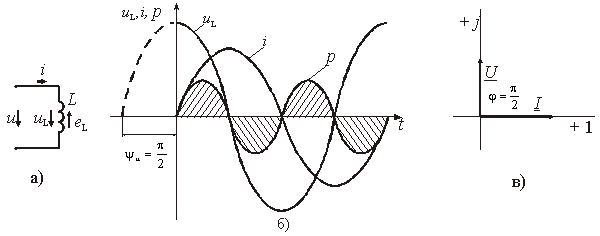
Из выражения видно, что начальная фаза напряжения ψ_u = π/2. Следовательно, синусоида напряжения на идеальной катушке индуктивности опережает синусоиду тока по фазе на угол π/2

φ = ψ_u – ψ_i = π/2 – 0 = π/2.

На практике, если напряжение по фазе опережает ток, говорят об индуктивном характере нагрузки. График мгновенных значений и векторная диаграмма тока и напряжения цепи с индуктивностью приведена на рисунке.

Амплитуда напряжения

U_m = ωLI_m,

откуда имеем

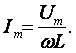
Действующее значение тока равно

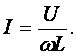
Это выражение представляет закон Ома для идеальной индуктивности.

Индуктивное сопротивление ωL выражается в омах и обозначается Х_L, т. е.

Х_L = ω L = 2 π f L.

Индуктивное сопротивление катушки имеет место только в том случае, когда происходит изменение тока во времени и зависит от скорости его изменения. При постоянном токе (f = 0) индуктивное сопротивление равно нулю.

Мгновенная мощность в индуктивном элементе

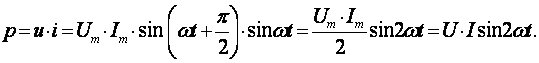
Амплитудное значение мгновенной мощности U·I называют реактивной мощностью

Q_L= U·I,

или учитывая, что U = X_L·I,

Q_L = X_L·I².

Реактивная мощность имеет размерность Baр.

Активная мощность в такой цепи, определяемая как средняя мощность за период, равна нулю, рис. б.