Дифференциальные уравнения движения идеальной жидкости. характеризуется градиентами давления , ,
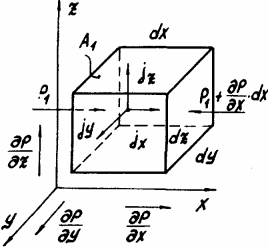
| Выделим в потоке жидкости прямоугольный элементарный объем со сторонами 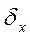 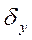 , ,  . В общем случае давление в различных точках жидкости неодинаково и его изменение . В общем случае давление в различных точках жидкости неодинаково и его изменение
|
характеризуется градиентами давления 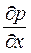 ,
, 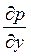 ,
,  . На выделенный объем действует массовая сила
. На выделенный объем действует массовая сила 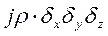 и равнодействующая поверхностных сил давления на его грани.
и равнодействующая поверхностных сил давления на его грани.
Уравнение движения выделенного объема вдоль оси 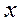 :
:
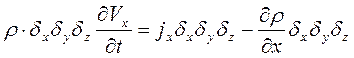
Аналогичные уравнения можно записать для движения объема вдоль других осей.
Полученная система дифференциальных уравнений в форме Эйлера выглядит следующим образом:

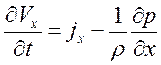
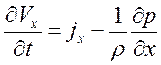
Подставляя 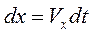 ,
,  ,
,  и суммируя уравнения, получаем общее уравнение гидродинамики для потока идеальной жидкости:
и суммируя уравнения, получаем общее уравнение гидродинамики для потока идеальной жидкости:
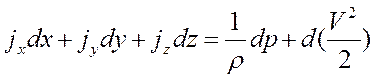
Общее уравнение гидростатики является частным случаем общего уравнения гидродинамики при V= 0.
Для частного случая, когда из числа массовых сил действует только сила тяжести, общее уравнение гидродинамики вырождается в уравнение Бернулли:
при 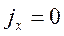 ,
, 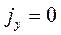 ,
, 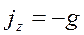 уравнение принимает вид:
уравнение принимает вид:
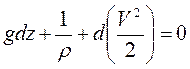
или  , следовательно,
, следовательно, 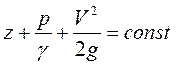 .
.
Дата добавления: 2015-10-13; просмотров: 693;
