Для идеальной движущейся жидкости сумма трех высот: нивелирной, пьезометрической и скоростной есть величина постоянная вдоль струйки.
Слагаемые в полученном выражении являются удельными энергиями (энергиями единичных массы и объема жидкости): z, - удельная энергия положения;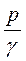 
- удельная энергия сжатия; 
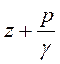потенциальная удельная энергия (гидростатический напор); 
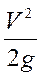- удельная кинетическая энергия (гидродинамический напор).
Таким образом, уравнение, впервые полученное Бернулли, является выражением закона сохранения механической энергии и означает, что полная удельная энергия (напор) в потоке идеальной жидкости постоянна.
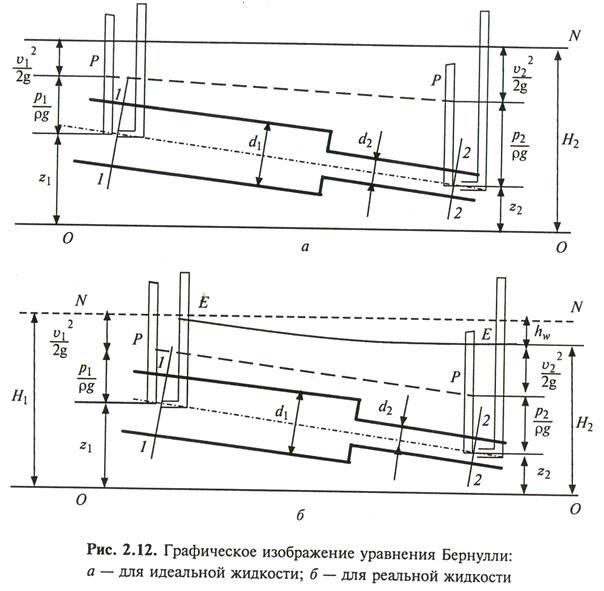
Графическая иллюстрация уравнения Бернулли для идеальной жидкости, показывающей изменение нивелирной, пьезометрической и скоростной высот вдоль струйки
Запишем уравнение Бернулли для потока реальной (вязкой) жидкости.
|
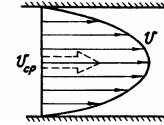
В условиях неравномерности распределения скоростей в сечении целесообразен переход к средним по сечению величинам скорости Vcp и полного напора Нср.
Элементарная струйка с сечением dA , скоростью V и напором Н имеет мощность dN=НgVdA. Подставляя в это выражение
и интегрируя по площади живого сечения - A , получаем выражение для суммарной мощности потока:
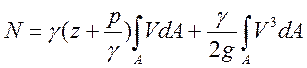
В то же время:
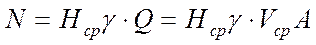
Решая совместно уравнения, получаем выражение для среднего по сечению напора вязкой жидкости:
где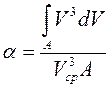 
называется коэффициентом неравномерности распределения скоростей в сечении. Этот коэффициент представляет собой отношение фактической кинетической энергии в сечении к этой энергии в потоке идеальной (невязкой) жидкости, двигающейся со скоростью Vcp . Значение коэффициента a зависит от формы эпюры распределения скоростей жидкости в живом сечении потока.
Учитывая суммарные потери напора на трение и вихреобразование å h: между некоторыми сечениями I и 2, напишем уравнение Бернулли для потока реальной (вязкой) жидкости:
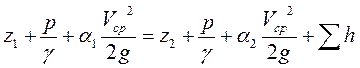
Уравнение Бернулли показывает, что с увеличением скорости жидкости в узких частях каналов гидростатическое давление падает.
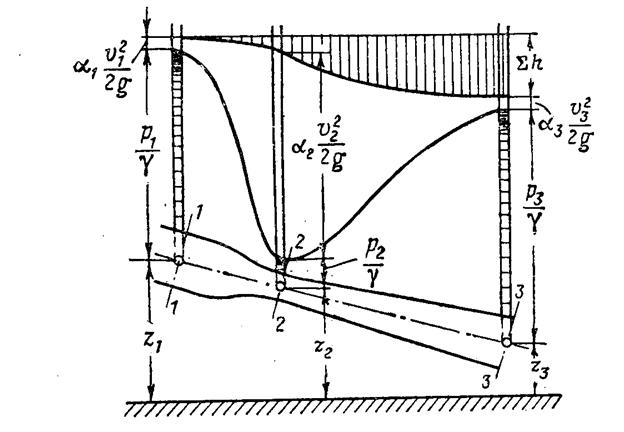
Графическая иллюстрация уравнения Бернулли для реального потока жидкости
Первый член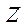 
выражает удельную потенциальную энергию положения жидкости в сечении потока, имеет размерность длины и называется геометрическим напором. Второй член 
выражает удельную потенциальную энергию давления жидкости и также имеет размерность длины. Энергия давления может быть измерена при помощи вертикальной пьезометрической трубки. Под действием давления 
жидкость поднимается в трубке на высоту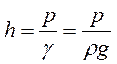 
, которая называется пьезометрическим напором. Иногда он называется статическим напором.
Третий член уравнения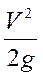 
выражает удельную кинетическую энергию движущейся жидкости. Этот член называется скоростным или динамическим напором.
Все напоры имеют размерность длины, поэтому уравнение Бернулли можно представить графически. При графическом представлении все напоры изображаются вертикальными отрезками, а их сумма – вертикалью, проведенной из произвольно выбранной плоскости О-О (нулевой уровень) до общей горизонтальной плоскости N-N (для идеальной жидкости). Если в рассматриваемых сечениях поместить открытые изогнутые стеклянные трубки, один конец которых направлен по оси потока навстречу сечению, то высота подъема жидкости в трубках будет соответствовать сумме пьезометрического и скоростного напоров.
Для реальной жидкости отрезок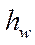 
будет характеризовать величину потерянного напора при ее движении от сечения 1-1 до сечения 2-2.
Сумма геометрического, пьезометрического и скоростного напоров называется гидродинамическим напором. Если соединить уровни жидкости в трубках, то получим нисходящую кривую Е-Е (для реальной жидкости), которая называется линией гидродинамического напора, или линией падения напора.
Используя уравнение Бернулли, можно определить скорость и расход жидкости, т.е. пропускную способность трубопроводов, а также время истечения жидкости и ее полный напор.
Дата добавления: 2015-10-13; просмотров: 1714;