Помощью решателей ode15,ode45

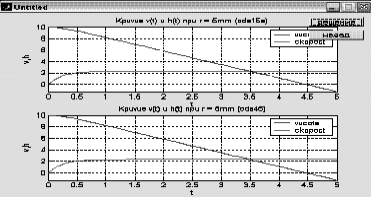
m-фа M-file f1.m:

function F1=pli(t,y)

mu=0.018; //динамическая вязкость воздуха

p1=800; //плотность шарика

p2=1.29; //плотность воздуха

c=0.4; //лобовое сопротивление шарика

g=9.8;

k=1000; //число разбиений

r=0.005; //радиус шарика

F1=[-y(2);9.8-9*mu/(r*r*p1*2)*y(2)-3*c*y(2)*y(2)*p2/(8*r*p1)];

m-файл для решения ДУ с помощью программы на языке программы MatLab M-file Sambo.m:

mu=0.018; //динамическая вязкость воздуха

p1=800; //плотность шарика

p2=1.29; //плотность воздуха

c=0.4; //коэффициент лобового сопротивления для шарика

g=9.8; //ускорение свободного падения

k=1000; //число разбиений

y(2)=0;y(1)=10;//начальные условия

x0=0;xk=5;//границы изменения времени

dx=(xk-x0)/k; //шаг интегрирования

r=0.005; //радиус шарика

x=x0;

subplot(2,1,1); //деление формы на 2 граф. окна

hold on; //обеспечивает продолжение вывода графиков в окно

for i=0:k-1

if y(1)<0 break,end;йл для решения ДУ с помощью решетелей

// вычисление коэффициентов для метода Рунге - Кутта

k11=-dx*y(2);k21=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*y(2)*y(2)*p2/(8*r*p1));

k12=-dx*(y(2)+k21/2);

k22=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k21/2)*(y(2)+k21/2)*p2/(8*r*p1)); k13=-dx*(y(2)+k22/2); k23=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k22/2)*(y(2)+k22/2)*p2/(8*r*p1));

k14=-dx*(y(2)+k23);k24=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k23)

*(y(2)+k23)*p2/(8*r*p1)); //расчёт разности

d1=(k11+2*k12+2*k13+k14)/6; d2=(k21+2*k22+2*k23+k24)/6;

//вычисление новых значений у1 и у2

y(11)=y(1)+d1; y(21)=y(2)+d2;

plot([x x+dx],[y(1) y(11)],’r’);plot([x x+dx],[y(2) y(21)],’b’),

x=x+dx; //новое значение х

y(1)=y(11); y(2)=y(21);

end;

grid on; //добавляет сетку к текущему графику

title(“Kpuvue v(t) u h(t) npu r = 5mm”); //установка на

графике титульной надписи

legend(“vucota”,’ckopoct’); //добавление к текущему графику xlabel('t');ylabel('v,h');

plot([0 5],[0 0],'k');axis tight;hold off; y(2)=0;y(1)=10;x0=0;xk=10;dx=(xk-x0)/k;

r0=0.002;rk=0.005;dr=(rk-r0)/3;

n=2;x=x0;r=r0;

subplot(2,1,2);hold on;

while r<=rk

for i=0:k-1

if y(1)<0 break,end;

k11=-dx*y(2);

k21=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*y(2)*y(2)*p2/(8*r*p1));

k12=-dx*(y(2)+k21/2);

k22=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k21/2)*(y(2)+k21/2)*p2/(8*r*p1)); k13=-dx*(y(2)+k22/2);

k23=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k22/2)*(y(2)+k22/2)*p2/(8*r*p1)); k14=-dx*(y(2)+k23);

k24=dx*(9.8-3*mu/(r*r*p1*2)-c*pi*(y(2)+k23)*(y(2)+k23)*p2/(8*r*p1));

d1=(k11+2*k12+2*k13+k14)/6; d2=(k21+2*k22+2*k23+k24)/6;

y(11)=y(1)+d1; y(21)=y(2)+d2;

plot([x x+dx],[y(1) y(11)],'r'); plot([x x+dx],[y(2) y(21)],'b');

x=x+dx; y(1)=y(11); y(2)=y(21); end;

x=x0; y(2)=0; y(1)=10;

r=r+dr; end;grid on;

title('Cemeuctvo v(t) u h(t): 2mm < r < 5mm');

legend('vucota','ckopoct');xlabel('t');ylabel('v,h');

plot([0 5],[0 0],'k');axis tight;hold off;

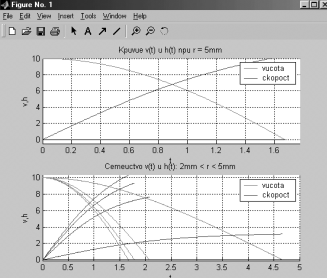
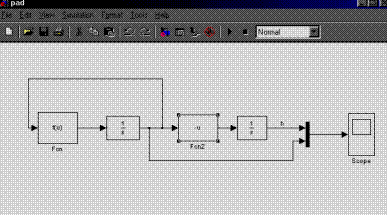
Графики зависимостей v(t),h(t) при r=5 mm и

семейство графиков для 2mm<R<5mm