Коэффициенты для расчета контрольных границ
| Размер выборки n | A2 | D3 | D4 |
| 1,880 | — | 3,267 | |
| 1,023 | — | 2,575 | |
| 0,729 | — | 2,282 | |
| 0,577 | — | 2,115 | |
| 0,483 | — | 2,004 | |
| 0,419 | 0,076 | 1 ,924 | |
| 0,373 | 0,136 | 1,864 | |
| 0,337 | 0,184 | 1,816 | |
| 0,308 | 0,223 | 1,777 |
На основе измерений и расчетов могут быть построены контрольные карты, пример которой приведен на рис. 12.1.
Когда на карте 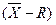 какая-то точка выходит за контрольную, границу или находится на ней, это означает неправильную настройку или разлаженность процесса.
какая-то точка выходит за контрольную, границу или находится на ней, это означает неправильную настройку или разлаженность процесса.
Центр группирования средних величин может быть смещен от, нормального положения. Обычно это легко устраняется настройкой оборудования.
Когда за контрольную границу регулирования перемещается точка на графике R, это означает, что увеличился разброс групп, случайные факторы нарушили нормальное течение процесса. Этот случай, как правило, более сложен для анализа, здесь необходимо усилить, входной контроль материалов, проверить технические характеристики оборудования.
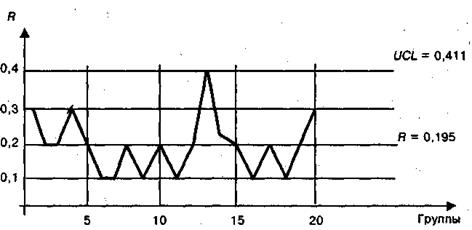
Рис. 12.1. Контрольная карта для толщины пластины
Выборочный контроль
По способу отбора изделий, подвергаемых контролю качества, различают сплошной (стопроцентный) и выборочный контроль.
Для сокращения затрат на контроль в крупносерийном и массовом производстве больших партий изделий (генеральной совокупности) контролю подвергают только часть партии — выборку.
Если уровень качества изделий в выборке соответствует установленным требованиям, то считают, что всю партию можно принять как годную. В противном случае партия бракуется.
В ряде случаев вся партия может быть ошибочно забракована, и это считается ошибкой первого рода, или риском поставщика. Ошибка противоположного свойства называется ошибкой второго рода или риском заказчика. Обе ошибки выражаются в процентах и оговариваются при совершении торговых сделок.
Если доля дефектных изделий в партии обозначить как q, то
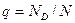
где N и ND — соответственно число дефектных деталей и их общее число.
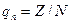
где qn — доля дефектных деталей в выборке;
Z— число бракованных деталей;
п — объем выборки.
Если бы генеральная совокупность и выборка имели распределение деталей по закону равной вероятности, то выборочный контроль значительно упростился бы, но, к сожалению, закономерности не совпадают и в общем случае:
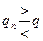
что и является причиной ошибок обоих родов при выборочном контроле.
Если qn > q, то возникает ошибка первого рода и, наоборот.
В разных случаях получают разные законы распределения вероятностей попадания годных и дефектных изделий в выборку, поэтому следует правильно выбирать математический аппарат для оценки качества контроля.
При выборочном контроле применяют в основном биноминальный, гипергеометрический, Пуассона и нормальный законы распределения.
Первые три являются законами распределения случайных величин и используются при контроле по качественному признаку, когда каждое отдельное испытание в серии имеет только два исхода: изделие годное или дефектное. Нормальный закон используется при контроле по количественным признакам.
Биноминальное распределение
Вероятность P(n,z) появления в выборке объемом и числа z дефектных изделий определяется по формуле:
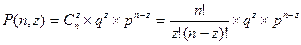
где q - вероятность появления брака;
р — вероятность появления годного изделия;
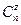 — сочетание из п элементов по z;
— сочетание из п элементов по z;
q и р — характеризуют устойчивость технологического процесса.
Допустим, что п = 30; q = 0,05 ; р = 0,95.
P (n, z) = P (30, z) — решение существует только в табличном виде и нужно задавать z в виде таблицы от 0 до z.
Пример.Вычислить в выборке число z дефектных изделий, где 0£ z<9; q = 0,05; р = 0,95; n = 30. Оценки вероятности приведены в табл. 12.3.
Таблица 12.3
Оценки вероятности обнаружения дефектных изделий
| Число дефектных изделий z | Вероятность Р (п, z) | Кумулятивная вероятность F(n,z) |
| 0,2146 | 0,2146 | |
| 0,3389 | 0,5535 | |
| 0,2586 | 0,8122 | |
| 0,127 | 0,9392 | |
| 0,0451 | 0,9844 | |
| 0,0124 | 0,9967 | |
| 0,0027 | 0,9994 | |
| 0,0005 | 0,9999 | |
| 0,0001 | 0,999998 | |
| 0,000001 | 0,999999 |
В правой части табл. 12.3 приведены результаты расчета так называемой кумулятивной вероятности, т.е., накопленной вероятности F(n,z). Величина F(n,z) позволяет оценить накопление дефектных изделий в выборке, их общее число равно:
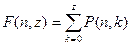
где k — число дефектных изделий, для которых выполняется расчет.
Допустим, что k = 4: Тогда (по данным таблицы):
F(30,4)= 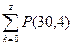 = 0,2146 + 0,3389 + 0,2586 + 0,1270 + 0,0451 = 0,9844.
= 0,2146 + 0,3389 + 0,2586 + 0,1270 + 0,0451 = 0,9844.
Кумулятивная вероятность показывает тенденцию наполнения выборки негодными деталями.
Данные таблицы являются начальной информацией, которая далее позволит полностью определить условия контроля с помощью выборки. На данном этапе это только информация для изучения. Графики плотности вероятности (а) и кумулятивной вероятности (б) показаны на рис. 12.2.
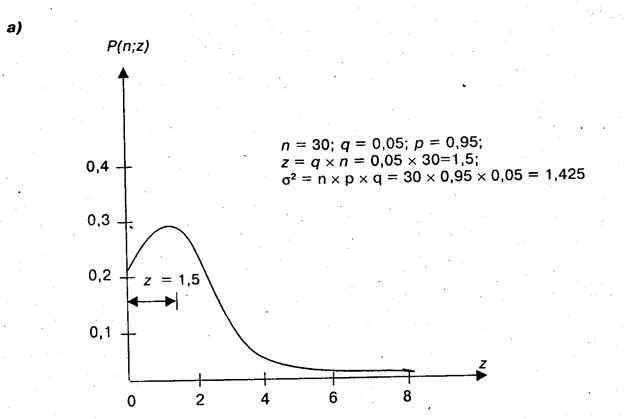
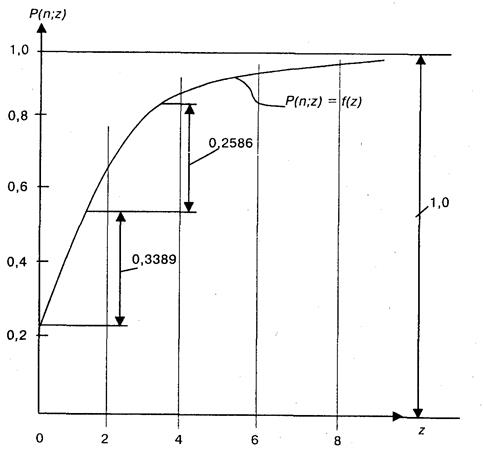
Рис. 12.2. Графики плотности вероятности (а)
и кумулятивной вероятности (б)
Гипергеометрическое распределение
Гипергеометрическое распределение характеризуется следующими зависимостями:
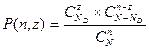 ;
; 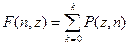 ;
;
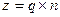 ;
; 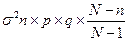 .
.
Характер графиков P(n,z) и F(n,z) не отличается от ранее рассмотренных. Сам закон более точно отражает ситуацию, когда выборка не возвращается в генеральную совокупность, что обычно имеет место на производстве.
Распределение Пуассона
Распределение Пуассона является предельным для биноминального распределения, когда вероятность (q £ 0,1) мала, число событий велико, а математическое ожидание 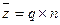 появления дефектных изделий является ограниченным числом.
появления дефектных изделий является ограниченным числом.
Это распределение часто называют законом распределения редких событий. При таких условиях формула
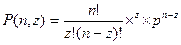
заменяется на формулу
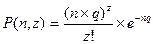
причем
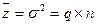
Таблица 12.4
Дата добавления: 2015-10-13; просмотров: 1034;
