ГОРИЗОНТАЛЬНЫХ ТРУБ РАЗЛИЧНЫХ ДИАМЕТРОВ,
ИЗГОТОВЛЕННЫХ ИЗ ОДИНАКОВОГО МАТЕРИАЛА
Конвективный теплообмен (теплоотдача) представляет собой процесс передачи тепла от твердой поверхности к газу или жидкости, или наоборот, от жидкости или газа к поверхности. Механизм теплоотдачи включает в себя теплопроводность внутри тонкого неподвижного слоя газа или жидкости у поверхности (пограничный слой) и конвекцию, т.е. способ передачи тепла, связанный с перемещением макрообъемов газа или жидкости.
Процесс теплопроводности в пограничном слое подчиняется законам, изложенным в работе №1.
Конвекция может быть свободной или вынужденной. При вынужденной конвекции перемещение различно нагретых объемов жидкости происходит под действием какого-либо постороннего источника движения (насоса, вентилятора, компрессора и т.д.)
Свободная конвекция возникает при соблюдении двух условий. 1. Наличия разности температур, и, следовательно, разности плотностей в объеме теплоносителя. В исследуемом случае разность температур создается между поверхностью трубы и окружающей средой.
2. Наличия поля тяготения. Необходимость этого условия становится ясной из следующих соображений: если в объеме теплоносителя, имеющего температуру t1, возник некоторый объем с температурой t2, то плотность последнего объема становится либо больше (если t2 < t1), либо меньше (t2 > t1) по сравнению с первоначальной. Тогда рассматриваемый объем, имеющий температуру t2, в силу закона Архимеда будет либо всплывать, либо опускаться относительно всего объема теплоносителя, т.к. он стал легче или тяжелее окружающих слоев газа или жидкости. Но понятия «легкий» и «тяжелый» справедливы в поле сил тяготения. При его отсутствии (в невесомости) свободная конвекция не возникает.
Одной из важнейших задач расчетов конвективного теплообмена является определение количества тепла, отдаваемого или принимаемого той или иной поверхностью теплообмена. Это количество тепла определяется по закону Ньютона:
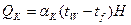 . (5.17)
. (5.17)
Здесь aК – основная характеристика конвективного теплообмена как при свободной, так и при вынужденной конвекции. Этот коэффициент носит название коэффициента теплоотдачи и представляет собой количество тепла, отдаваемое или принимаемое единицей поверхности в единицу времени при разности температур между поверхностью и теплоносителем в один градус. Следовательно, его размерность Дж/(м2×с×град)=Вт/м2×град. Определение величины aК представляет значительные трудности, т.к. aК зависит от многих факторов, например, геометрии поверхности, свойств теплоносителя, температуры и т.д.
Величина aК определяется обычно из критериальных уравнений, полученных на основании теорий подобия и размерностей. Например, теплоотдача в условиях вынужденной конвекции описывается уравнением
Nu = c Ren Prm , (5.18)
а в условиях свободной конвекции
Nu = c Сrn Prm , (5.19)
в частности для газов,
Nu = c (Сr Pr)n . (5.20)
В уравнениях (5.18), (5.19), (5.20) Nu- критерий Нуссельта, который служит для определения коэффициента теплоотдачи aK:
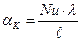 (5.21)
(5.21)
Понятие о критериях подобия, входящих в уравнение (5.18), (5.19), (5.20) вводится при помощи специальной теории, называемой теорией подобия.
Их физический смысл объяснен в табл. 5.4.
Таблица 5.4
Основные критерии подобия
| Наименование критерия | Формула | Что характеризует |
| 1. Критерий Нуссельта | 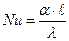
| Интенсивность теплообмена на границе стенка-жидкость |
| 2. Критерий Рейнольдса | 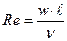
| Соотношение сил инерции и сил вязкости в потоке жидкости |
| 3. Критерий Грасгофа | 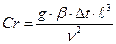
| Соотношение подъемных сил и вязкости |
| 4. Критерий Прандтля | 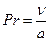
| Физические свойства жидкости |
В критериях Нуссельта, Грасгофа, Рейнольдса содержится величина, называемая определяющим линейным размером 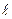 . Выбор этого размера для каждого конкретного случая производится так, чтобы был учтен тот путь, который проходит нагреваемый (охлаждаемый) теплоноситель около поверхности. Например, воздух вдоль вертикальной трубы проходит путь, равный длине трубы, а горизонтальную трубу воздух обтекает по диаметру. Значит, в первом случае
. Выбор этого размера для каждого конкретного случая производится так, чтобы был учтен тот путь, который проходит нагреваемый (охлаждаемый) теплоноситель около поверхности. Например, воздух вдоль вертикальной трубы проходит путь, равный длине трубы, а горизонтальную трубу воздух обтекает по диаметру. Значит, в первом случае 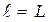 трубы, а во втором
трубы, а во втором 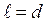 .
.
В упомянутые критерии подобия входят также свойства теплоносителя: l - коэффициент теплопроводности, n - коэффициент кинематической вязкости и b - коэффициент объемного расширения. Эти параметры, а также критерий Pr выбираются из табл. 3. приложения. Коэффициент объемного расширения для воздуха может также определятся из выражения
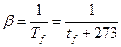 . (5.22)
. (5.22)
Таблица 5.5
Коэффициенты в критериальных уравнениях
| CrPr | c | N |
| от 0 до 5×102 | 1,18 | 0,125 |
| от 5×102 до 2×107 | 0,54 | 0,25 |
| от 2×107 и выше | 0,135 | 0,33 |
Следует отметить, что количество тепла Q, передаваемое трубой в окружающее пространство, определяется по мощности, потребляемой электронагревателем. Это количество тепла передается окружающей среде путем теплообмена и радиации (излучения).
Коэффициент теплоотдачи aK вычисляется (для последующего определения критерия Нуссельта) по доле конвективной составляющей теплового потока:
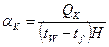 . (5.23)
. (5.23)
В свою очередь, конвективная составляющая теплового потока QK определяется как полный тепловой поток за вычетом радиационной составляющей QИ:
QK = Q – QИ , (5.24)
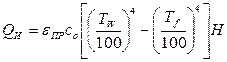 , (5.25)
, (5.25)
где eПР – приведенная степень черноты (см. табл. 1 приложения), Со = 5,67 Вт / (М2 К 2) – коэффициент излучения абсолютно черного тела. Необходимо вычислить коэффициент теплоотдачи a по классическому уравнению (5.23) и сравнить его с опытом.
5.6.3. Экспериментальная установка
Схема экспериментальной установки аналогична рис. 5.4 (работа № 2). Отличия заключаются в том, что в данной работе обе трубы выполнены из одинакового материала и имеют различные диаметры d1 = 15 мм и d2 = 20 мм. Длины труб одинаковы и равны L = 460 мм.
Таблица 5.6
Расчетная таблица к работам № 3и 4
| Наименование величин | Расчетные формулы | Режим 1 | Режим 2 | |||
| Элемент 1 | Элемент 2 | Элемент 1 | Элемент 2 | |||
| Температура поверхности трубы | Tw | - | ||||
| Температура окр. среды | Tf | - | ||||
| Тепловой поток | Q | - | ||||
| Поверхность трубы | H | H = p d 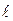
| ||||
| Величина лучистого теплового потока | QИ | 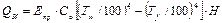
| ||||
| Конвективная составляющая теплового потока | QK | Qk = Q - QИ | ||||
| Коэффициент теплоотдачи опытный | aK | 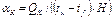
| ||||
| Коэффициент кинематической вязкости | nf | - | ||||
| Критерий Прандтля | Pr | - | ||||
| Коэффициент теплопроводности | lf | - | ||||
| Коэффициент объемного расширения | b | 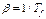
| ||||
| Критерий Нуссельта | Nu | 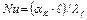
| ||||
| Критерий Грасгофа | Gr | 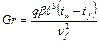
| ||||
| Произведение (Gr × Pr) | - | - | ||||
| Расчетный критерий Цуссельта | Nup | 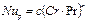
| ||||
| а) показатель | n | |||||
| б) постоянная (выбирается из табл. 6.2) | c | |||||
| Коэффициент теплоотдачи (расчетный) | ap | 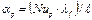
|
Дата добавления: 2015-10-13; просмотров: 1279;
