Моделей с использованием технологии VaR
При реализации любого инвестиционного проекта возникают непредвиденные расходы, которые следует учитывать при формировании портфеля инвестиционных ресурсов в виде резервного фонда. Мировой опыт инвестиционной деятельности показывает, что размер резервного фонда должен формироваться в размере 15% от суммы инвестиционных затрат.
Возможность реального прогнозирования инвестиционных рисков является одним из важных условий эффективного управления процессом вложения средств в развитие материально-технической базы организаций. В предлагаемом подходе к моделированию инвестиционного риска оценка вероятности убытков за любой период производится по функции распределения случайной величины T. При этом предполагается, что известна вероятность не получения прибыли в текущем периоде. Оценка вероятности наступления неблагоприятного периода для реализации инвестиционного проекта в результате воздействия внешних и внутренних факторов может быть получена путем оценивания регрессионных зависимостей от макроэкономических факторов или задана экспертно. В нашем случае при проведении расчетов вероятность получения убытка определена экспертным путем.
Если допустить, что вероятность события заключающегося в получении убытка в результате использования инвестиционных ресурсов постоянна во времени (по крайней мере, в течение периода, сопоставимого с горизонтом инвестиционного проекта). Тогда, как следует из свойств пуассоновского потока, случайная величина Т, равная интервалу между двумя событиями, распределена экспоненциально (формула 11.1):
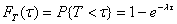 (11.1)
(11.1)
где – интенсивность потока,
τ – заданный интервал времени.
Зная вероятность получения убытка за шаг расчета, 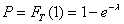 , найдем интенсивность потока по формуле 11.2:
, найдем интенсивность потока по формуле 11.2:
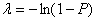
(11.2)
что позволяет определить вероятность потерь в течение периода реализации проекта (h) по формуле 11.3:
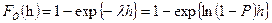 (11.3)
(11.3)
где h=H/360,
H – срок (в днях).
Рассмотрим финансовые вложения в инвестиционный проект C в некоторый момент времени t: C ={Sj, Hj, Pj, rj, zj}, где j –порядковый номер финансовых и материальных затрат, j=1..N; Sj – суммы инвестиционных расходов по периодам реализации проекта; Hj – окончания реализации проекта; Pj – вероятность получения убытка в отчетном периоде; rj – стоимость инвестиционных ресурсов; zj – уровень потерь в случае получения убытков.
Потери LP по инвестиционному проекту равны сумме потерь полученных в отдельных инвестиционных периодах (формула 11.4):
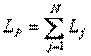
(11.4)
Найдём числовые характеристики потерь LP в предположении о независимости распределения убытков по отдельным кредитам:
Математическое ожидание потерь по инвестиционному проекту (формула 11.5):
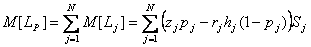
(11.5)
Дисперсия потерь инвестиционного проекта определяется по формуле 11.6:
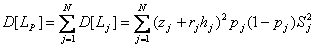
(11.6)
Стандартное отклонение потерь по инвестиционному проекту определяется по формуле 11.7.
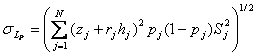
(11.7)
где pj – вероятность убытка после горизонта расчета.
Величина M[LP] определяет ожидаемый уровень потерь и необходимый размер резервов для их покрытия, 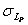 используется для оценки непредвиденных потерь и, соответственно, требований к сумме инвестиционного резервного фонда.
используется для оценки непредвиденных потерь и, соответственно, требований к сумме инвестиционного резервного фонда.
Для оценки максимально возможных потерь с заданной доверительной вероятностью произведем построение теоретической функции на основе закона нормального распределения, где параметрами расчета функции будут математическое ожидание и стандартное отклонение размера убытка по инвестиционному проекту.
Предлагается следующий алгоритм моделирования:
1.Для каждого инвестиционного вложения j определяется вероятность получения потерь за период времени равный рассматриваемому горизонту. В данном случае примем период равный 9 месяцам или 270 дней.
2. Производится расчет параметров функции распределения потерь : математическое ожидание и стандартное отклонение.
3. Строится функция распределения убытка и определяем наибольший ожидаемый уровень убытков по инвестициям с заданной вероятностью. В нашем случае вероятность примем 95 %.
4. Определяем размер необходимых резервов и величину необходимого инвестиционного капитала.
Применение рассмотренного подхода проиллюстрируем на инвестиционного проекта ,состоящего из инвестиционных потоков на сумму S=6 629 372 тыс.р. В качестве исследуемого инвестиционного портфеля выступает проект, разбитый на условные периоды реализации проекта со средними вероятностями убытка, шагом расчета и стоимостью ресурсов. Исходные данные представлены в таблице.11.1
Таблица 11.1 - Исходные данные для расчета вероятности дефолта за
рассматриваемый период времени
| Номер периода инвест. вложений | Суммы инвест. затрат по периодам | Интервал м/у потоками дни | Вероятность потерь % (Pj) | Коэффициент риска | Стоимость ресурсов,% | ||
| 5 200 270,00 | 12,00 | 0,9 | 30,5 | ||||
| 450 764,00 | 9,70 | 0,9 | 32,5 | ||||
| 612 119,00 | 8,00 | 0,9 | 32,5 | ||||
| 19 685,00 | 8,00 | 0,9 | 32,5 | ||||
| 35 498,00 | 8,00 | 0,9 | 32,5 | ||||
| 81 152,00 | 8,00 | 0,9 | 31,0 | ||||
| 4 825,00 | 6,00 | 0,9 | 32,5 | ||||
| 6 004,00 | 2,00 | 0,9 | 32,5 | ||||
| 1 545,00 | 7,00 | 0,9 | 32,0 | ||||
| 16 677,00 | 5,00 | 0,9 | 32,5 | ||||
| 65 753,00 | 20,00 | 0,9 | 32,5 | ||||
| 135 080,00 | 25,00 | 0,9 | 30,5 | ||||
Необходимо оценить ожидаемую прибыль и максимально возможные убытки с 95% доверительной вероятностью за горизонт, равный периоду реализации проекта.
Рассчитаем вероятность убытка за горизонт расчета с учетом интервала между инвестиционными потоками (табл. 11.2):
Таблица 11.2 - Вероятность убытков по инвестиционному проекту
| Номер периода инвестиционных вложений | Вероятность убытка за горизонт расчета с учетом сроков инвестиционных затрат Номер периода инвестиционных вложений, pj |
| 0,09 | |
| 0,02 | |
| 0,02 | |
| 0,02 | |
| 0,01 | |
| 0,05 | |
| 0,02 | |
| 0,00 | |
| 0,04 | |
| 0,01 | |
| 0,09 | |
| 0,16 |
Математическое ожидание и стандартное отклонение убытков портфеля за горизонт, рассчитанные на основе соотношения (11.3), равны:
M[LP] = -925 651,20 тыс.р; 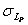 = 1 681 210,49 тыс.р.
= 1 681 210,49 тыс.р.
Таким образом, ожидаемый объем прибыли за горизонт составит 925 651,20 тыс.р. Начисленная процентная прибыль за этот период при отсутствии дефолтов, рассчитанная как сумма процентов по кредитам , равна 1 302 507,411 тыс р. Объем резервов можно найти как разницу начисленной и ожидаемой прибыли, что составляет 376856,21 тыс.рублей.
На основе рассчитанных параметров строим функцию распределения на (рис.4.1) и находим максимально возможные убытки с 95% доверительной вероятностью (95% квантиль теоретической функции распределения): QLP 95% = 1 750 000 тыс. р. (26,4% от объема портфеля).
Величина необходимого экономического капитала рассчитывается как разность между максимально возможными убытками и сформированными резервами (1 750 000 тыс.рублей -376 856,21тыс.рублей) и составляет 1 373 143,79 тыс.рублей (20,7 % от объема портфеля).
Используя данную методику банк может с заданной долей вероятности спрогнозировать максимально возможные убытки и соответственно заранее рассчитать необходимые параметры минимизации данных убытков. В частности для сравнения резерв по кредитам на 1.01.2004 года Филиал составляет 123 969,00 тыс.р., в то время как расчетный 376856,21 тыс.р. С одной стороны может показаться,что это свидетельствует о ухудшении показателей банка ,так как мы вынуждены связывать средства в резерве на покрытие возможных убытков . Однако, в мировой практике принято, зарубежными банками используется методика, согласно начисление резерва происходит на любую задолженность, включая и стандартную. это обусловлено в первую очередь осторожной политикой банка в области недопущения непредвиденных потерь . При этом можно заметить ,что ситуация с начислением большего резерва по кредитам выгодна для банков и тем ,что позволяет снизить размер налогооблагаемой прибыли так как отчисления в резерв относятся на расходы банка до налогообложения и включаются в затраты в полном размере независимо от величины полученных доходов. По мере возврата и выдачи кредитов данные средства будут высвобождаться или же будет происходить доначисление резерва.
Дата добавления: 2015-10-13; просмотров: 660;
